
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математичні моделі для аналізу на мікрорівніСодержание книги
Поиск на нашем сайте Математичними моделями на мікрорівні є диференціальні рівняння в частинних похідних або інтегральні рівняння, що описують поля фізичних величин. Інакше кажучи, на мікрорівні використаються моделі з розподіленими параметрами. У якості незалежних змінних у моделях можуть фігурувати просторові змінні Характерними прикладами моделей можуть служити рівняння математичної фізики разом із заданими крайовими умовами. Приклад 1 Рівняння теплопровідності:
Приклад 2 Рівняння дифузії:
Крайові умови включають початкові умови, що характеризують просторовий розподіл залежних змінних у початковий момент часу, і граничні, що задають значення цих змінних на границях розглянутої області у функції часу.
Методи аналізу на мікрорівні У САПР рішення диференціальних або інтегро-диференціальних рівнянь із частковими похідними виконується чисельними методами. Ці методи засновані на дискретизації незалежних змінних – їхньому представленні кінцевою множиною значень в обраних вузлових крапках досліджуваного простору. Ці точки розглядаються як вузли деякої сітки, тому використовувані в САПР методи – це сіткові методи. Серед сіткових методів найбільше поширення одержали два методи: метод кінцевих різностей (МКР) і метод скінченних елементів (МСЕ). Звичайно виконують дискретизацію просторових незалежних змінних, тобто використають просторову сітку. У цьому випадку результатом дискретизації є система звичайних диференціальних рівнянь для нестаціонарної задачі або система алгебраїчних рівнянь для стаціонарної. Нехай необхідно вирішити рівняння
У методі кінцевих різностей алгебраізація похідних по просторових координатах базується на апроксимації похідних кінцево-різницевими виразами. При використанні методу потрібно вибрати кроки сітки по кожній координаті й вид шаблона. Під шаблоном розуміють множину вузлових точок, значення змінних у яких використовуються для апроксимації похідної в одній конкретній точці.
Рис. 3. Приклади шаблонів для одномірних і двовимірних задач
Приклади шаблонів для одномірних і двовимірних задач наведені на Рис. 3. На цьому рисунку кружком більшого діаметра позначені вузли, у яких апроксимується похідна. Чорними точками позначені вузли, значення фазової змінної в яких входять в апроксимуючий вираз. Число, записане біля вузла, дорівнює коефіцієнту, з яким значення фазової змінної входить в апроксимуюче вираження. Так, для одномірних шаблонів у верхній частині малюнка показана апроксимація похідної
Шаблони для двовимірних задач у нижній частині Рис.3 відповідають наступним кінцево-різнистним операторам: · лівий рисунок:
· середній рисунок:
· правий рисунок:
Тут Метод скінченних елементів заснований на апроксимації не похідних, а самого рішення
де При цьому мова йде про апроксимації рішення в межах скінченних елементів, а з урахуванням їхніх малих розмірів можна говорити про використання порівняно простих апроксимуючих виразів
з якої потрібно знайти вектор Цю задачу (визначення · метод коллокаций, у якому, використовуючи (3.24), формують
· метод найменших квадратів, заснований на мінімізації квадратів нев’язок у · метод Гальоркіна, за допомогою якого мінімізуються в середньому по області нев’язка зі спеціальними ваговими коефіцієнтами, що задаються. Найбільше поширення МСЕ одержав у САПР машинобудування для аналізу міцності об’єктів. Для цієї задачі можна використовути розглянутий підхід, тобто виконати алгебраізацію вихідного рівняння пружності (рівняння Ламе). Однак більш зручним у реалізації МСЕ виявився підхід, заснований на варіаційних принципах механіки.
|
|||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 й час
й час 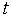 .
.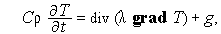
 — питома теплоємність,
— питома теплоємність,  — густина,
— густина,  — температура,
— температура,  — час,
— час,  — коефіцієнт теплопровідності,
— коефіцієнт теплопровідності,  — кількість теплоти, виділюваної в одиницю часу в одиниці об’єму.
— кількість теплоти, виділюваної в одиницю часу в одиниці об’єму.
 — концентрація часток,
— концентрація часток,  — коефіцієнт дифузії.
— коефіцієнт дифузії.

 й
й 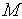 — диференціальні оператори,
— диференціальні оператори,  — фазова змінна,
— фазова змінна,  — вектор незалежних змінних,
— вектор незалежних змінних,  (
( ) і
) і  (
(
 в точці
в точці  , і зазначеним шаблонам при їхньому перегляді ліворуч-праворуч відповідають апроксимації
, і зазначеним шаблонам при їхньому перегляді ліворуч-праворуч відповідають апроксимації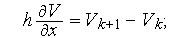


 — крок дискретизації по осі
— крок дискретизації по осі  .
.


 — значення
— значення  в точці
в точці  ; прийняті однакові значення кроків
; прийняті однакові значення кроків 

 — вектор-рядок невизначених коефіцієнтів,
— вектор-рядок невизначених коефіцієнтів, 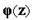 — вектор-стовпець координатних функцій (опорних функцій), заданих так, що задовольняються граничні умови.
— вектор-стовпець координатних функцій (опорних функцій), заданих так, що задовольняються граничні умови. (наприклад,
(наприклад,  — поліноми низьких ступенів). У результаті підстановки
— поліноми низьких ступенів). У результаті підстановки 
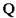 .
. рівнянь із невідомим вектором
рівнянь із невідомим вектором  :
:



