
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простір станів, передатна функція електронних системСодержание книги
Поиск на нашем сайте
Основою для проведення аналізу властивостей існуючих і спрямованого синтезу нових електронних систем із заданими характеристиками є їхній математичний опис або математична модель. Основним питанням, з яким приходиться зіштовхуватися при складанні математичної моделі, є питання її адекватності реально існуючому об'єкту. Обрана математична модель повинна, з одного боку, відбивати властивості реального об'єкта з необхідним ступенем точності, а, з іншого - бути не занадто складною, що визначає одержання кінцевого результату доступними засобами. У загальному випадку елементи, використовувані для побудови підсилювальних пристроїв, мають нелінійні характеристики, причому їхні параметри залежать як від часу, так і від зовнішніх умов експлуатації. Тому точний математичний опис електронних систем в тому числі і підсилювальних пристроїв досить громіздкий і базується на використанні систем нелінійних диференціальних рівнянь, параметри яких залежать від часу та різних зовнішніх збурюючих впливів. Однак у більшості практичних випадків цими залежностями можна зневажити і з точки зору математичного опису розглядати підсилювальний пристрій як безперервну лінійну стаціонарну систему з зосередженими параметрами і детермінованим законом керування. Безперервною називається система, у якій усі сигнали її компонентів є безперервними функціями часу або частоти; лінійною – система, для якої справедливий принцип суперпозиції; стаціонарною – система, параметри і характеристики якої не залежать від часу. Детермінованим називається закон керування, що припускає однозначний зв'язок між вхідним впливом і відповідним значенням вихідного параметра. Для опису безперервних лінійних, стаціонарних систем дістали поширення математичні моделі в вигляді однорідних та неоднорідних диференційних рівнянь, форсованих та нефорсованих передатних функцій в операторній формі запису та формі перетворення Лапласа та їх еквіваленти в просторі змінних стану. Для стаціонарної системи передатна функція визначається як відношення зображень Лапласа при нульових початкових умовах:
де для, так званих, фізично реалiзуємих систем d ≤ n. Коефіцієнти ai , bj вiдомi i постiйнi. Якщо виключити випадок так названих скорочуваних нулів та полюсiв, передатна функцiя однозначно вiдповiдає диференцiальному рiвнянню:
Введемо позначення:
Одержимо наступний опис в просторі станів (Y 1, Y 2, …, Yn) Y = AY + Bu, (1.3) де:
Y – змiннi стану, u – вектор керування. Рівняння з матрицею називають рівнянням в формі Фробенiуса. Часто вимірюванню доступна лише величина x, а величини Другий опис форсованої електронної системи з передатною функцією в просторі станів:
Y = де: x – вектор входу. Матриця А має попередній вираз, а матриця B= [ b 1, b 2, …, bn ] T, а спiввiдношення (1.5) можна розглядати як скалярне рівняння спостерігання. Запишемо iншi рiвняння в просторі станів, еквiвалентнi в розумiннi передатної функцiї системи. Введемо систему рiвнянь:
де координати (Y 1, Y 2, …, Yn) вiдмiннi вiд розглянутих раніше. Без обмеження спiльностi можна прийняти, що m = n (якщо m < n, то вiдповiдне число коефiцiєнтiв в чисельнику передаточної функції дорівнює нулю). Якщо величини bi в рівняннях (1.3) зв'язанi з коефiцiєнтами передаточної функцiї спiввiдношеннями (1.5), то передатна функцiя з новими змінними стану співпадає з розглянутою раніше:
Ще одне подання в просторі станів можна одержати шляхом розкладу передатної функції на прості дроби. Якщо корені характеристичного рівняння:
(власні числа матриці А) прості i дорівнюють
дe Cn (v=0,1,...,n) визначаються по вiдомим формулам. Спiввiдношення еквiвалентне слiдуючому виразу в оригiналах:
де:
Таким чином, в цьому просторi станiв система описується векторним рiвнянням:
дe:
e = [1,1,...,1]т – вектор, елементами якого являються одиницi i скалярне рiвняння спостерiгання. Для математичного опису підсилювального пристрою в функції часу можна скористатися системою диференціальних рівнянь з постійними коефіцієнтами. Реакція підсилювального пристрою на деякий вхідний вплив, вихідна система диференціальних рівнянь може бути приведена до одного рівняння високого порядку з миттєвими значеннями вхідних збурень, прикладених до різних входів підсилювального пристрою та постійними коефіцієнтами, що містять суми і добутки параметрів елементів, що входять до складу підсилювального пристрою (наприклад R, L, C).
Рівняння (1.1) дозволяє одержати передатну функцію підсилювального пристрою по обраному вхідному збуренню. При одержанні W 1(p) передбачається, що Uвх 2 =0. Таке допущення справедливе, тому що ми припустили, що наш підсилювальний пристрій є лінійною системою, для якої справедливий принцип суперпозиції, тобто реакція на суму впливів дорівнює сумі реакцій на кожний окремо узятий вплив. За аналогією, з раніше проробленим, передатну функцію можна представити у виді:
Отримані передатні функції називаються передатними функціями в операторній формі. Поряд з ними широко використовуються передатні функції у формі зображень Лапласа, тобто у виді відносин не оригіналів функцій, а їхніх зображень, отриманих відповідно до вираження:
де s – комплексний параметр перетворення Лапласа, що має розмірність частоти (1/с); L – покажчик перетворення Лапласа; x(t) – задана функція; X(s) – зображення заданої функції x(t);
Слід зазначити, що для випадку стаціонарних систем, тобто систем, у яких параметри елементів не залежать від часу, передатна функція у формі перетворень Лапласа може бути отримана з передатної функції в операторній формі простою заміною перемінної p на s. Ця зовнішня подібність порозумівається тим, що для зображення від похідної справедливе вираження:
Для випадку x (0)=0 маємо: Таким чином, вираження (1.11) еквівалентне вихідному диференціальному рівнянню системи (1.1) тільки у випадку нульових початкових умов. У противному випадку вираженням (1.11) для математичного опису підсилювального пристрою користатися не можна. Пояснюється це таким чином. У випадку, якщо багаточлен, що описує поводження системи, та багаточлени впливу збурення містять загальні нулі (множники), останні при обчисленні передатної функції скорочуються. Тому (при довільних початкових умовах) за отриманими передатними функціями не можна точно відновити вихідне диференціальне рівняння. Отже, не можна правильно описати поводження підсилювального пристрою.
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.170.65 (0.011 с.) |

 (1.1)
(1.1) . (1.2)
. (1.2)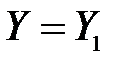 ,
, 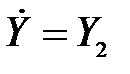 , …,
, …,  ,
, .
. Rn:
Rn:
 ,
, ,
, ,...
,...  можуть бути лише оцiненi на основі того чи іншого алгоритму. В таких випадках використання таких рівнянь виявляється незручним.
можуть бути лише оцiненi на основі того чи іншого алгоритму. В таких випадках використання таких рівнянь виявляється незручним. = AY + Bx, (1.4)
= AY + Bx, (1.4) +
+  x, (1.5)
x, (1.5) (1.6)
(1.6) (1.7)
(1.7)
 , то
, то ,
, ,
,
 ,
, ,
, . (1.8)
. (1.8) ,
,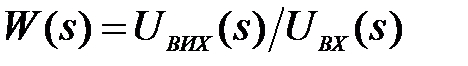 . (1.9)
. (1.9) (1.10)
(1.10) (1.11)
(1.11)


