
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інженерна методика розрахунку систем автоматичного регулювання технологічних параметрівСодержание книги
Поиск на нашем сайте Агрегатно-модульні комплекси поперечно-клинової прокатки вміщують: системи автоматичного регулювання частот обертання прокатних валків, правильної рамки, транспортуючих роликів і подачі не обертаючогося прутка на задану довжину, а також позиційні - положення обертача подачі проволоки з бунта і супорта з прокатним валком. Вимоги до швидкодії автоматичних систем суперечні, оскільки збільшення швидкодії приводить до того, що система добре пропускає високочастотні перешкоди, посилюючи їх по потужності і створюючи недопустимі перевантаження об'єкту регулювання, знижує точність профілів, а його зменшення не дозволяє повністю відтворити сигнал, що також збільшує помилку регулювання. Оптимізація швидкодії систем автоматичного регулювання технологічних параметрів забезпечує мінімально можливу відносну усталену помилку. Для розрахунку оптимальних параметрів форсованої ланки другого порядку потрібно визначити: ступінь регулярності процесу і параметр затухання на основі автокореляційної функції, а також відношення дисперсій процесу і перешкоди, враховуючи, що остання визначається не тільки класом точності технічних засобів, але й викривленням інформації, наприклад, за рахунок ексцентриситету валків. Задача забезпечення оптимальної швидкодії системи вирішується шляхом введення ланок динамічної корекції, які вмикаються або в прямий канал регулювання (послідовна корекція), або в зворотні зв'язки, які охоплюють всі або частину функціонально необхідних елементів не скоректованої системи (паралельна корекція). В сучасних автоматизованих електроприводах повсюдно застосовуються системи керування з послідовною корекцією, побудовані по принципу підлеглого регулювання параметрів і основані на застосуванні активних елементів динамічної корекції - операційних підсилювачів, що грають роль регуляторів. Силова частина електроприводу структурно представлена складеною з послідовного з'єднання ланок, кожна з яких характеризується однією великою постійною часу. Таким чином, вся система регулювання складена із декількох контурів, в кожному з яких можна виділити регулятор і об'єкт регулювання. Для регулювання об'єкту, що являє собою добуток інерційних ланок з великою і малою некомпенсованими постійними часу, застосовується ПІ-регулятор з передаточною функцією
де Т0, Т - постійні часу випередження та інтегрування. Передавальна функція розімкненого контура з врахуванням суми некомпенсованих малих постійних часу контура
де Характер перехідного процесу контуру регулювання визначається співвідношенням постійних часу інтегруючої ланки Т1, яка входить у склад регулятора, і суми малих постійних часу контуру Тμ. Настроювання регулятора по модульному критерію, яке широко поширене, забезпечується при Т = 2ТμК0. Порівнюючи одержані коефіцієнти з оптимальними по критерію мінімуму середньоквадратичної помилки (квазіоптимальне рішення) отримали, що незалежно від постійної часу Т оптимальне значення показника затухання дорівнює 0,707 і забезпечується при Розрахунок оптимальних передаточних функцій регуляторів систем оснований на представленні незмінної частини передаточної функції прокатної кліті і виконавчих механізмів найпростішими моделями, наведеними у главі 1. Задача полягає у синтезі простих легко реалізованих алгоритмів керування. На рис. 12.1. представлені приклади реалізації квазіоптимальної передаточної функції завадостійкої замкненої системи по каналу переміщення верхнього валка. Замкнута система автоматичного регулювання переміщенням верхнього валка включає незмінну частину – без інерційну прокатну кліть, редуктор, що описується інтегральною динамічною ланкою, і виконавчий механізм. Якщо динамічну модель привода описують інерційною ланкою першого порядку, то застосовується регулятор з пропорційно-інтегральним алгоритмом перетворення, якщо ланкою другого порядку (коливальним або аперіодичним), то регулятор має про" порційно-інтегрально-диференційний алгоритм. Якщо параметри настроювання ПІ-алгоритму регулятора внутрішнього контуру регулювання по мал.12.1, а вибрати із умови
де КМ - коефіцієнт передачі електропривода; ТИ1 - постійна часу інтегрування. Замикаючи внутрішній контур, отримуємо
Розімкнене коло другого контуру має передатну функцію у вигляді
Замикаючи другий контур з врахуванням коефіцієнтів К0 і К3, отримали передатну функцію
де К0- оптимальний коефіцієнт передачі по каналу зміна положення валка висотний розмір; ТИ2- постійна часу інтегрування. Аналогічний вираз отримано за рис. 12.1, де застосовується ПІД - алгоритм регулювання, а його параметри вибрані із умов
де ТЭ,ТМ - електромагнітна і електромеханічна постійні часу електропривода, Параметри функції (12.4) зв'язані з квазіоптимальною (12.4) наступними співвідношеннями:
Звідси постійна часу ізодрому і коефіцієнт передачі регулятора визначаються із співвідношень
Якщо редуктор не забезпечує оптимальне значення часу ізодрому, то можлива корекція за рахунок зміни коефіцієнта передачі підсилювача з коефіцієнтом передачі КИ. В першому випадку коефіцієнт передачі ізодромного регулятора дорівнює
Для ПІД - алгоритму перетворення коефіцієнт передачі визначається аналогічно попередньому, а постійна часу випередження дорівнює
Коефіцієнт передачі квазіоптимальної динамічної системи зв'язаний з коефіцієнтом передачі об'єкта і задатчика співвідношенням К=К0К3. (12.9) Тоді оптимальне значення коефіцієнта передачі задатчика дорівнює К3= К/К0. (12.10) Отже, для реалізації квазіоптимальної передаточної функції замкненої системи позиціювання потрібна наявність двох регуляторів - пропорційного і ПІД або ПІ в залежності від динамічних властивостей приводу натискного пристрою кліті. Наприклад, для умов прокатки автоободу ЗІЛ-130 параметри диференційованого випадкового процесу дорівнюють ψ =1,5 і α =1, тоді К =0,54; Тμ =0,43; ξ =0,6 при μ =0,5Гц, Т =0,86 с. Коефіцієнт передачі кліті К0 =0,7. Редуктор забезпечує ТИ2 =100 с. Електромеханічна і електромагнітна постійні електродвигуна дорівнюють ТМ =0,3 с; ТЭ =0,15 с, коефіцієнт передачі КМ = 0,13. Оптимальні параметри: задатчика К3 =1,08, пропорційного регулятора КИ = 100 /(2х0,6х0,86) = 96,89, ПІД регулятора КИ = (2х0,3х0,6) /(0,5х0,86) = 0,84, ТИ 1= (0,5х0,86) /(2х0,6) = 0,36 с,
Отримані параметри забезпечують реалізацію квазіоптимальної передаточної функції (12.4). Аналогічний розрахунок параметрів системи керування положенням обертача і частотою обертання рамки правильної машини. Параметри пропорційно-інтегрально-диференційного регулятора вибираються із співвідношень ТдТИ=ТЭТМ; КПТИ=ТМ. Постійна часу замкнутого внутрішнього контура дорівнює Т/К. Квазіоптимальні параметри за виразом (12.5) зв'язані з отриманими співвідношеннями Т3=Tf/Kf; T4=TИ/КП Тоді квазіоптимальні параметри настроювання регуляторів дорівнюють Наприклад, для даних табл. 12.1 при α = і постійні часу квазіоптимальної передаточної функції дорівнюють: Т3 =58 с, Т4 =50 с. Параметри двигуна з редуктором: ТЭ =0,1с; ТМ =0,25 с; КП =0,8; Тφ =80 с. Квазіоптимальні параметри регуляторів у відповідності з отриманими формулами дорівннюють: Кφ =1,38; КИ =0,07; ТИ =3,53 с; Якщо електромагнітна постійна часу двигуна постійного струму значно менше ніж електромеханічна, то передавальна функція за кутом повороту має - вигляд
і співпадає з квазіоптимальною, якщо Т3= Тφ, а ТМ=Т4. В цьому випадку оптимальні параметри мають вигляд:
Відношення постійних часу дорівнює
при α =0 Розглянемо реалізацію оптимальної передаточної функції для правильної машини (рис. 12.1). Внутрішній контур регулювання сили струму містить регулятор з пропорційно" інтегральним законом. із умови компенсації електромагнітної постійної часу параметри регулятора зв'язані співвідношенням ТЭ = КИТИ, тоді постійна часу внутрішнього контуру дорівнює ТИ/КЭ. Порівнюючи постійні часу квазіоптимального рішення і отриманого, знаходимо
Рисунок 12.1. Реалізація квазіоптимальної передаточної функції замкненої системи автоматичного регулювання частоти обертання правильної машини
Оптимальні параметри настройки регулятора дорівнюють
Для реалізації квазіоптимальної функції замкненої системи задатчик повинен мати коефіцієнт передачі, який отримали в результаті стохастичного синтезу. По каналу зміна частоти обертання зміна товщини прокатна кліть являється без інерційною ланкою з коефіцієнтом передачі К0. Для реалізації оптимальної передаточної функції зробимо розмикання системи, тоді реалізація отриманого в главі 2 рішення можуть бути представлені у вигляді трьох варіантів, відмінних динамічними характеристиками електричного привода прокатної кліті. Якщо привід є без інерційним, то у внутрішньому контур: застосовується регулятор з пропорційно-інтегральним алгоритмом перетворення, а в наступному контурі інтегральний алгоритм. Параметри регуляторів вибираються із наступних співвідношень: Т1=КТИ; Т3 =ТИ2 /К0КМ; Т4=ТИ(1 + ККМ). (12.10) На основі відомих параметрів Т1, Т3, Т4, К0, КМ визначаються невідомі оптимальні параметри настроювання інтегрального і пропорційно інтегрального регуляторів: ТИ2=Т3К0КМ, ТИ1 = Т4+ КМ Т1; К = Т1/(Т4+ КМ Т1). (12.11) Якщо електричний привід апроксимовано аперіодичною ланкою першого порядку, то для пропорційно-інтегрального регулятора у внутрішньому контурі параметри рівні КТИ1=ТМ, тоді передавальна функція замкненої системи дорівнює аперіодичній ланці з постійною часу ТИ1/КМ. Розглянемо синтез регулятора і варіанти реалізації оптимальної передаточної функції розімкнутої системи автоматичного регулювання діаметра прокатної деталі. Параметри функції зв¢язані співвідношеннями
Звідси отримали оптимальні настроювання пропорційного регулятора. Коефіцієнт передачі - При виконанні умови КИ1ТИ1=Т0 отримали передатну функцію замкненої системи внутрішнього контура з одиничним коефіцієнтом передачі і постійною часу ТИ1/К0. Тоді передавальна функція системи співпадає з оптимальною, якщо
Тоді оптимальні параметри настроювання регуляторів мають такий вигляд
Їх реалізація забезпечує оптимізацію динамічної системи по критерію мінімуму середньоквадратичної помилки. Наприклад, якщо ψ =1; α =і, отримали, що Тμ =0,54; ξ =0,707; К =0,42; Т1μ =0,43; тому Т3μ =0,58; Т4μ =0,13. Тоді при К0 =0,7; Т0 =0,2с; μ =1Гц оптимальні настроювання регуляторів дорівнюють: КИ2 =0,74; КИ1 =0,57; ТИ2 =0,58 с; ТИ1 =0,35 с. Якщо врахувати швидкодію тиристорного джерела струму, тоді об'єкт регулювання включає послідовне з'єднання двох аперіодичних ланок, а параметри пропорційно-інтегрально-диференційного регулятора мають наступний вигляд:
Постійна часу замкнутого внутрішнього контуру дорівнює ТИ /(КПК0). Тоді із умови рівності отриманих значень оптимальним у відповідності з передаточною функцією (12.5)
Отже, оптимальні параметри настроювання регуляторів мають наступний вигляд
Наприклад, у задачі оптимального синтезу для диференційованого випадкового процесу, коли ψ =1, α =1, отримали Т4μ =0,5; Т1μ =0,43; Т3μ =0,58. При К0 =0,7; КП =2; Т0 =0,2 с; ТП =0,05 с; μ=1Гц отримані наступні оптимальні настроювання: КИ1 =0,74; ТИ1 =0,58с; К =0,36; ТИ =0,7 с; То =.0,014 с - регуляторів з ПІ і ПІД алгоритмами роботи. На рис. 12.2. приведені варіанти реалізації квазіоптимальної передаточної функції розімкнутої системи. Параметри об'єкта регулювання - прокатної кліті по каналу зміна зазору між валками - висотний розмір профіля зв'язані з квазіоптимальними параметрами наступним чином
При заданому коефіцієнті передачі виконавчого механізму КМ постійна часу ізодрому інтегрального регулятора зв'язана з постійною часу форсування об'єкта співвідношенням.
Рисунок 12.2. Реалізація квазіоптимальної передаточної функції розімкнутої системи переміщення валка при пропусканні через зону деформацій електричного струму
Якщо виконавчий механізм описується аперіодичною ланкою першого порядку, то коефіцієнт передачі пропорційно-інтегрального регулятора дорівнює
Для виконавчого механізму, який описується ланкою другого порядку (коливальною або аперіодичною), застосовується пропорційно-інтегрально-диференційний алгоритм перетворення з наступними настроюваннями: коефіцієнт передачі К = ТМ /(Т 01 КМ), постійна випередження На станах гарячої прокатки важливим технологічним параметром являється температура поверхні прокату. На вхід вимірювача надходить корисний сигнал - випромінювання заготовки і перешкода у вигляді різного підсвічування. Збільшення початкової температури підвищує швидкодію вимірювача. Передавальна функція фотоелектричного пірометра по каналу зміна яскравості світлового потоку - вихідна напруга має вигляд, що співпадає з квазіоптимальною функцією (13.4)
де Т - постійна часу; ξ - відносний коефіцієнт затухання; К - коефіцієнт передачі. Для умов прокатки універсального штаба на універсальному стані 1200 Дніпродзержинського металургійного комбінату ступінь регулярності процесу як відношення резонансної частоти до параметру затухання дорівнює 1,213. Відношення дисперсії процесу до дисперсії перешкоди у смузі процесу дорівнює 10. Тоді оптимальні значення добутку постійної часу на параметр затухання Тμ=0,31; ξ=0,68; К=0,94. Для параметра затухання 3,3 Гц постійна часу дорівнює оптимальному значенню, тоді резонансна частота дорівнює 4,125 Гц. Таким чином, для умов процесу μ= 3,3 Гц; ψ=1,25; α=10 практично виконуються оптимальні умови вимірювання температури. Проте при збільшенні відносного рівня перешкод, наприклад, при α =100 оптимальні параметри функції (13.4) дорівнюють Тμ=0,18; ξ=0,7; К=0,99. Тоді для задоволення оптимальних умов вимірювання необхідно збільшити в 1,72 рази швидкодію, що можливо при збільшенні початкової температури волоска лампи зворотного зв'язку до 930 0С, що зменшує коефіцієнт передачі в 1,3 рази і для наближення його до оптимального треба збільшити його в 1,36 рази. Якщо зміни додаткового початкового розігріву волоску лампи зворотного зв'язку недостатньо, то необхідно змінити номінальне значення інтегруючої ємності силового блоку. Зі збільшенням ємності постійна часу зменшується, а параметр відносного затухання дещо збільшується. В цілому з збільшенням рівня перешкод необхідно зменшити початкову температуру (струм) лампи зворотного зв'язку або збільшити абсолютне значення інтегруючої ємності в катодному колі посилювача вихідного каскаду.
|
||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

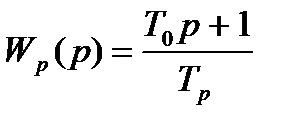 , (12.1)
, (12.1)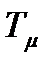 має вигляд
має вигляд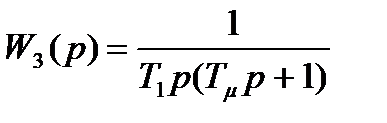 , (12.2)
, (12.2)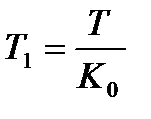 ; К0 - коефіцієнт передачі об'єкта.
; К0 - коефіцієнт передачі об'єкта.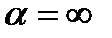 , оскільки значення коефіцієнта передачі дорівнює одиниці і не залежить від ступеня регулярності процесу.
, оскільки значення коефіцієнта передачі дорівнює одиниці і не залежить від ступеня регулярності процесу.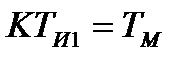 , тоді передатна функція розімкненого кола внутрішнього контуру дорівнює
, тоді передатна функція розімкненого кола внутрішнього контуру дорівнює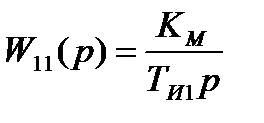 (12.1)
(12.1)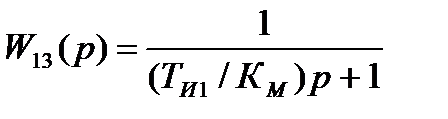 (12.2)
(12.2)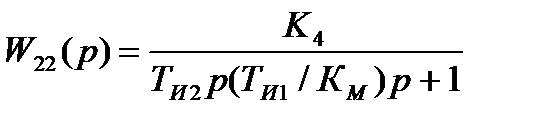 (12.3)
(12.3) (12.4)
(12.4)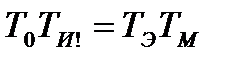 ;
; 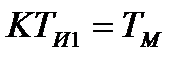 (12.5)
(12.5)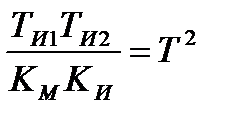 ;
; 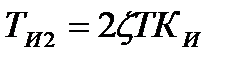 (12.5)
(12.5)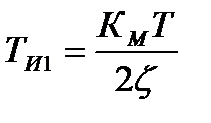 ;
; 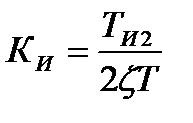 (12.6)
(12.6)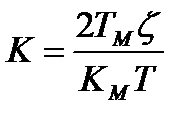 . (12.7)
. (12.7)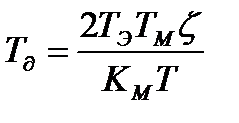 . (12.8)
. (12.8)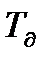 = (2х0,15х0,3х0,6) /(0,5х0,86) = 0,12 с.
= (2х0,15х0,3х0,6) /(0,5х0,86) = 0,12 с.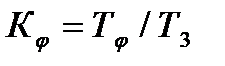
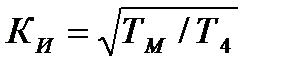 ,
, 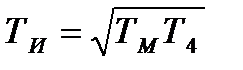
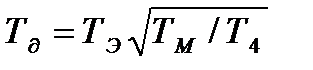
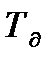 =0,007 с. Для реалізації передаточної функції замкненої системи задатчик має коефіцієнт передачі рівний отриманому в результаті синтезу, тобто К=0,42.
=0,007 с. Для реалізації передаточної функції замкненої системи задатчик має коефіцієнт передачі рівний отриманому в результаті синтезу, тобто К=0,42.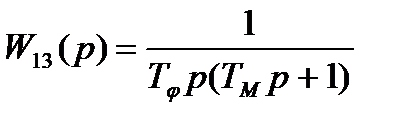 (12.5)
(12.5)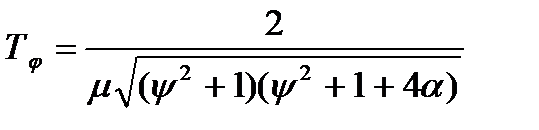 ,
,  . (12.6)
. (12.6)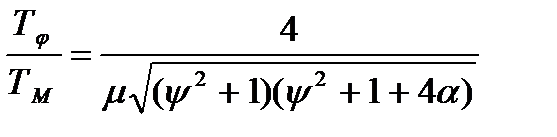 (12.7)
(12.7)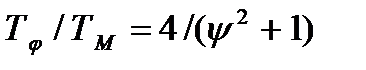 , отже, при ψ ≥1,73 Тφ = ТМ, а при
, отже, при ψ ≥1,73 Тφ = ТМ, а при  1,73 - навпаки. Збільшення відношення дисперсій процесу і перешкоди зменшує - значення ступеня регулярності, коли виконується умова Тφ=ТМ. Оскільки передаточне число редуктора чисельно дорівнює Т, то це дає можливість оцінити оптимальне передаточне число, наприклад, при μ =6.10-3Гц, ψ = 1, α = 1 отримали, що Тφ =99с, ТМ =83,3с. Отже, оптимальне передаточне число редуктора дорівнює 99.
1,73 - навпаки. Збільшення відношення дисперсій процесу і перешкоди зменшує - значення ступеня регулярності, коли виконується умова Тφ=ТМ. Оскільки передаточне число редуктора чисельно дорівнює Т, то це дає можливість оцінити оптимальне передаточне число, наприклад, при μ =6.10-3Гц, ψ = 1, α = 1 отримали, що Тφ =99с, ТМ =83,3с. Отже, оптимальне передаточне число редуктора дорівнює 99.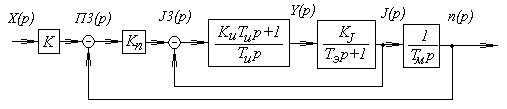
 ;
; 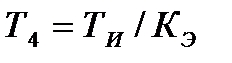 . (12.8)
. (12.8)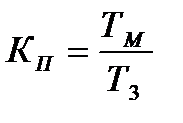
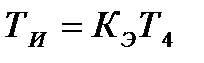
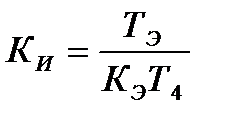 (12.9)
(12.9) ;
; 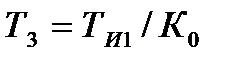
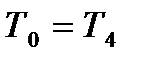 . (12.12)
. (12.12)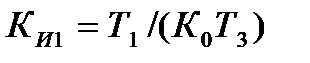 , постійна часу
, постійна часу 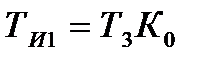 . Для реалізації цих. умов необхідно, щоб Т4=Т0, якщо цю умову виконати неможливо, так як Т4 визначається параметрами випадкових процесів, а Т0 - зовнішнім впливом, то реалізацію оптимального рішення можна виконати, використовуючи два пропорційно-інтегральних регулятора.
. Для реалізації цих. умов необхідно, щоб Т4=Т0, якщо цю умову виконати неможливо, так як Т4 визначається параметрами випадкових процесів, а Т0 - зовнішнім впливом, то реалізацію оптимального рішення можна виконати, використовуючи два пропорційно-інтегральних регулятора.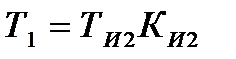 ;
; 
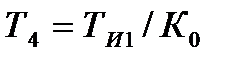 . (12.13)
. (12.13)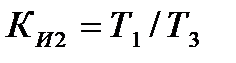 ;
; 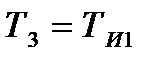
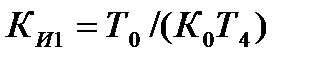
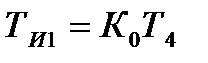 . (12.14)
. (12.14)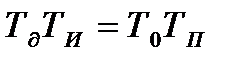
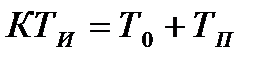 (12.15)
(12.15)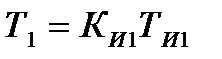
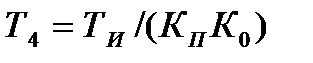 . (12.16)
. (12.16)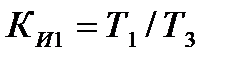 ,
, 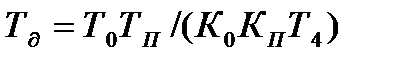 ,
, ,
, 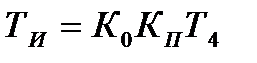 . (12.17)
. (12.17)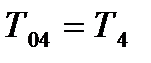 ;
; 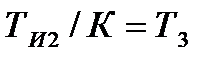 . (12.18)
. (12.18)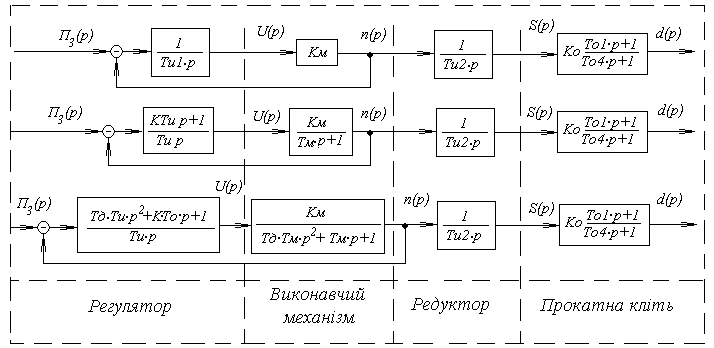
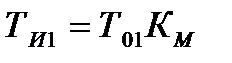 . (12.19)
. (12.19)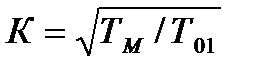 . (12.20)
. (12.20)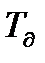 =(ТЭТМ)/(Т01КМ). Наприклад, при Т 01=0,05 с, КМ =2, ТМ =0,4 с, ТЭ =0,1 с отримаємо ТИ 1= 0,1 с, К =2,
=(ТЭТМ)/(Т01КМ). Наприклад, при Т 01=0,05 с, КМ =2, ТМ =0,4 с, ТЭ =0,1 с отримаємо ТИ 1= 0,1 с, К =2,  =0,4 с.
=0,4 с.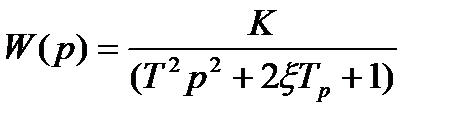 (12.21)
(12.21)


