
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Z - перетворення дискретного сигналуСодержание книги
Поиск на нашем сайте
Дискретний сигнал і його спектр описуються формулами:
Проведемо у формулі (9.1) заміну: Тоді формула прийме вигляд:
Вираз (9.33) одержав назву z-претворення або z-зображення дискретного сигналу x[n]. Якщо почати підсумовування з n = 0, той вираз
є одностороннє z-претворення. Воно застосовується для сигналів x[n]=0 при n<0. Можна вказати на зв'язок z-претворення з перетворення Лапласа дискретного сигналу
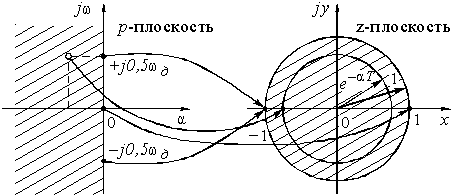
яке легке одержати з (9.1), поклавши j2pf = p. Очевидно, що z = eрT або p = T-1ln z. Ці формули встановлюють зв'язок між точками в площинах p=+ji, z = x+jy (рис. 9.17.). Якщо покласти а = 0, то ми переміщатимемося по осі jw в площині р. При переході в z-площину точки уявної осі jw розташовуватимуться на одиничному колі z = ejwT. Причому, точка j0 на р-площині переходить в точку z = +1 на речовинній осі z-площини, а точки ±j0,5w д – у точку z = –1. Це означає, що точки відрізка (-j0,5w д ÷ j0,5w д) р-площини проектуються в точки на одиничному колі z-площини.
Рисунок 9.17. Перенесення точок з p-площини в z-площину.
Оскільки функція Точкам лівої р-півплощини відповідають крапки усередині одиничного кола z-площини, а точкам правої p-полуплощини – крапки зовні цього кола. Як знайти дискретний сигнал по його z-претворенню. Можна скористатися зворотним z-претворенню (подібно тому як ми користуємося зворотним перетворенням Лапласа):
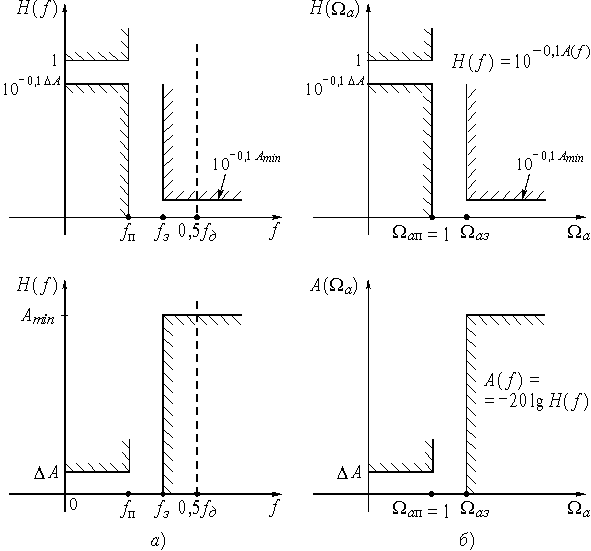
де інтеграція ведеться по замкнутому контуру в z-площини. Інший спосіб полягає в тому, щоб розкласти функцію X(z) у статичний ряд за ступенями z-1. Тоді коефіцієнти при ступенях z-1 будуть, відповідно до формули (9.2), відліків дискретного сигналу x[n]. Дискретний ланцюг може здійснювати будь-які операції: фільтрацію сигналу, коректування характеристик і т.п., тобто виконувати функції будь-якого аналогового ланцюга. Зокрема, при синтезі дискретних частотних фільтрів потрібно знайти такі коефіцієнти передавальної функції, частотна характеристика якої відповідала б нормам ослаблення фільтру в смугах пропускання і не пропускання (мал. 9.18). Визначення коефіцієнтів – це задача апроксимації. Відомий цілий ряд методів її рішення. Найпоширенішим є наступний метод. Спочатку розраховують аналоговий НЧ-прототип і одержують його передавальну функцію H(p), потім шляхом заміни комплексної змінної p=Ф{z} переходять від H(p) до передавальної функції дискретного ланцюга H(z).
Рисунок 9.18. Частотні характеристики фільтрів.
Використовування стандартного перетворення z=e pT або p=(1/T)lnz не приведе до дробово-раціональної функції. Тому для ФНЧ застосовують білінійне перетворення
(g – деякий постійний множник), яке є першим наближенням стандартного перетворення при розкладанні його в ряд Тейлора:
З розкладання (9.5) виходить, що необхідно вибирати g = 2/T. Проте, далі ми покажемо, що зручніше брати інші значення коефіцієнта g. Білінійне перетворення (9.6) переводить всі крапки з лівої напівплощини змінної p в крапки на одиничному колі площини z. Отже, якщо був стійкий аналоговий ланцюг, буде стійкою і дискретна. У цифровому фільтрі зберігання і обробка чисел (представлених, як ми вже знаємо, в двійковому коді) здійснюється в пристроях (елементах пам'яті, помножувачах, суматорах) з кінцевим числом розрядів. Тому розрахунок цифрового фільтру, крім визначення передавальної функції H(z) фільтру і його структурної схеми (див. вище) включає також розрахунок розрядів АЦП і ЦАП і розрядів резисторів оперативної пам'яті (помножувачів, суматорів). Крім того, при розрахунку цифрового фільтру передбачають розрахунок масштабних множників, що вводяться в схему для запобігання переповнювання регістрів фільтру, а також перевірку стійкості фільтру. Одним з найбільш розповсюджених методів переходу від аналогової до цифрової передатної функції є білінійне перетворення, що дозволяє зіставити кожній комплексній крапці s-площини тільки одну визначену крапку комплексної z-площини. Через нелінійне співвідношення між цифровою й аналоговою частотами цей метод дає кращі результати тільки на нижніх частотах, тому він найбільше підходить при проектуванні фільтрів нижніх частот. Білінійне перетворення визначається в таким чином:
де T- період дискретизації сигналів. Для одержання необхідної функції H(z) цифрового фільтру необхідно зробити заміну:
Полюси цифрового фільтру можна знайти через полюси відповідного аналогового фільтра за співвідношенням:
З цього вираження видно, що полюси з лівої (стійкої) s-напівплощини відображуються усередині одиничної окружності на z-площині, а полюси з правої (хитливої) s-напівплощини відобразяться на z-площині поза одиничним колом. Вибір періоду дискретизації завжди впливає на координати полюсів і нулів у комплексної z-площині. Використовуючи рівняння (9.9) можна побудувати графік залежності руху полюсів на площині в залежності від періоду дискретизації T (рис. 9.19).
Рисунок 9.19 – Вплив періоду дискретизації T на положення полюсів у z-площині
При збільшенні періоду дискретизації від 1 до ∞ корені рухаються до точки (-1;0), групуючись навколо неї. Аналогічна ситуація спостерігається при зменшенні періоду дискретизації від 1 до -∞, коли корені рухаються до точки (1;0), групуючись навколо неї. При цьому дійсна частина кореня буде прагнути до -1 чи 1 відповідно, уявна частина буде прагнути до 0. Ця властивість накладає деякі умови на вибір періоду дискретизації, наприклад, при виборі періоду дискретизації 10±d точність обчислень при білінійному перетворенні полінома 2-го порядку повинна бути не менш 2d знаків. При білінійному перетворенні поліномів більш високих порядків точність обчислень підвищується в n раз (де n- порядок полінома). Недостатня точність білінійного перетворення може привести до великої похибки і втрати інформації. Зазначена властивість найбільш актуальна для фільтрів високих порядків n≥10, особливо еліптичних. При підвищенні порядку фільтра найближчі комплексно-сполучені корені розташовуються дуже близько до уявноої осі, тобто дійсна частина прагне до нуля, що у свою чергу підвищує показник коливності. Якщо при розрахунку цифрового фільтра не можна забезпечити задану точність, то зважується задача вибору компромісного періоду дискретизації. Таблиця. 9.1. - Форумули заміни для різних типів фільрів.
Як випливає з малюнка 9.1, період дискретизації варто вибирати так, щоб корені на z - площині знаходилися як найближче до дійсної осі (T≈2), що дозволить значно спростити розрахунок фільтра за рахунок зменшення необхідної точності обчислень. Якщо позначити період дискретизації фільтра Tф, а період дискретизації вхідного сигналу Твх, то частота зрізу проектованого фільтра буде дорівнює:
На АЧХ отриманого фільтра одиниці по осі частот потрібно розділити на Твх для переходу до дійсних частот. Таким чином, як би розтягується сигнал у часі, а після фільтрації повертається у вихідний стан. Контрольні запитання
1. Чим є аналогові, дискретні і цифрові сигнли? 2. Як розрахувати z-зображення дискретного сигналу? 3. Що таке радіус збіжності? 4. Яка імпульсна характеристика для нерекурсивних (для рекурсивних) фільтрів: кінцева або нескінченна? 5. Як впливає період дискретизації на динаміку електронних систем? 6. Що являть собою фільтри із змінною частотою дискретизації? 7. На які групи ділять способи реалізації цифрових фільтрів? 8. Навести структурну схему біквадратного НІХ-фільтра. 9. Порівняти КІХ та НІХ фільтри. 10. В чому основна відмінність рекурсивних фільтрів? 11. Чому при реалізації рекурсивних фільтрів обмежується порядок фільтра? 12. Про що свідчить теорема В.А. Котельникова? 13. Як розрахувати z-зображення дискретного сигналу? 14. Що таке радіус збіжності?
|
|||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 502; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.173.197 (0.011 с.) |

 ; (9.1)
; (9.1)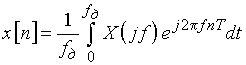 . (9.2)
. (9.2) .
. . (9.3)
. (9.3) . (9.4)
. (9.4) ,
,
 періодична, то подальші відрізки осі jw на р-площині такої ж довжини знов проектуватимуться на одиничне коло.
періодична, то подальші відрізки осі jw на р-площині такої ж довжини знов проектуватимуться на одиничне коло.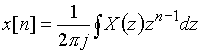 ,
,
 . (9.5)
. (9.5) . (9.6)
. (9.6) (9.7)
(9.7) (9.8)
(9.8)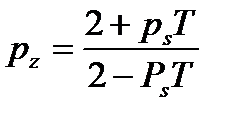 (9.9)
(9.9)

 . (9.10)
. (9.10)


