
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операції факторизації та сепарації.Содержание книги
Поиск на нашем сайте
Вхідний сигнал Х(t) динамічної системи має вигляд: Х (t) = Λ (t) + N (t). (3.1) Потрiбний вихiдний сигнал У(t), який виражається як деяке відоме (бажане) перетворення вектору корисного сигналу Λ(t), має вигляд: У (t) = Н { Λ (t)}, (3.2) де: Н { Λ (t)} - матричний оператор. На основі узагальненого рівняння Вiнера-Хопфа фізично реалiзуємi керованi багатовимiрнi системи в областi зображення мають вид:
де: Wj (p) – вектор передаточних функцiй системи; Sj(p) – вектор взаємних спектральних щiльностей вхiдних та ідеальних вихiдних сигналiв;
У формулi (3.3) аргумент (р) випущений. Вектор Матриця включає спектральнi щiльностi вхiдних сигналiв, якi представляють собою парнi функцiї. Парну функцiю, як і матрицю S, можна представити в виглядi добутку двох матриць, одна з яких З врахуванням операції факторизації рiвняння (3.3) має вид:
Лiва частина рiвняння (3.4) представляє собою матрицю, функцiї якої мають всi полюси в лiвiй напiвплощинi, оскiльки обидвi матрицi Пiсля операцiї сепарацiї маємо:
де: [S–]-1 – обернена матриця факторизованiй матрицi щiльностей входу Х; Sj – матриця взаємних спектральних щiльностей мiж iдеальним сигналом входу Λ та виходу У; {Sj[S–]-1}+ – сепарована матриця. Рiвняння (3.4) з врахуванням (3.5):
Обидва члени лiвої частини (3.6) мають функцiї, якi мiстять всi полюси в лiвiй напiвплощинi, а обидва доданки правої частини складенi з матриць, якi влючають функцiї, що мiстять всi полюси в правiй напiвплощинi. З врахуванням вимог аналiтичностi та обмеженостi матриць S та Sj можна показати, що права частина рівняння (3.6) обертається в нуль. Тому в кiнцевому видi вихiдне рiвняння для статистичного синтезу має вигляд:
Схема синтезу багатовимiрної системи керування мiстить наступнi операцiї: факторизацiю рацiональної матрицi спектральних щiльностей, знаходження обернених матриць, обчислення матриці { Sj [ S –]-1} та виконання операцiї сепарацiї, знаходження результуючої матрицi передаточних функцiй. Факторизацiя рацiональної матрицi без врахування умов фiзичної реалiзовностi фiльтру виконується достатньо просто. В протилежному випадку рiшення задачi достатньо складне та громiздке, потребує великої спостерегливостi. В рядi задач пiдвищення точностi розмiрiв матрицю S можна привести до дiагональної форми, дякуючи чому багатовимiрну систему можна представити у виглядi суми h одновимiрних пiдсистем. Спектральна матриця h - вимiрного вхiдного процесу є симетрична матриця:
Використовуючи ортогональне перетворення, одержимо дiагональну матрицю V у виглядi (ω – випущений): V = де Тодi: V =
де що визначаються з умови: (S - де Х – вектор вхiдних впливiв у виглядi матриці стовпця h×1; I – одинична матриця. Прирiвнявши нулю визначник |S-
Наприклад у випадку двовимiрного об'єкту iз (3.10) та (3.11) виходить:
Коренi характеристичного рівняння:
являються елементами головної дiагоналi матриці:
Таким чином, при виконаннi окремих умов матриця має достатньо простi елементи, якi визначаються комбiнацiями спектральних щiльностей корисного сигналу та перешкод. Розглянемо одновимiрне рiвняння Вiнера-Хопфа в комплекснiй областi, яке має вигляд (аргумент р – випущений): SxxW - Syl = f, (3.19) де Sxx – спектральна щiльнiсть суми корисного сигналу Sl та перешкод SN; Syl – взаємна спектральна щiльнiсть iдеального вхiдного сигналу та вихiдного. Пiсля факторизацiї спектральної щільності:
Доведено, що: W = І являє собою унiверсальний алгоритм визначення передаточних функцiй стацiонарних лiнiйних оптимальних систем. Однак слабкою ланкою є визначення взаємної спектральної щiльностi, яка вважається вiдомою. Тому її слiд визначити або експериментально, але тодi треба знати корисний сигнал на входi динамiчної системи, або аналiтично, наприклад, за теоремою Вiнера-Хiнчина, коли для некорельованих корисного сигналу та перешкод можна записати: Syl =Н Sl. (3.22) З врахуванням того, що Sl = Sxx - SN, де SN - спектральна щiльнiсть перешкод, з рiвняння (3.2) маємо:
Права частина рiвняння (3.23) дорiвнює нулю, тому оптимальна передаточна функцiя динамiчної системи має вигляд:
Якщо Syl =H(Sl + SNl), де SNl – взаємна спектральна щiльнiсть перешкоди та корисного сигналу, то з рiвняння (3.20) виходить що:
В випадку наявностi комплексно-спряжених коренiв вихiдний вираз для операцiї сепарацiї у вiдповiдностi з (3.24) має вигляд:
У випадку iснування дiйсних коренiв у вiдповiдностi з виразом (3.2), коли Н = 1, визначили вихiдне рiвняння для виконання операцiї сепарації:
яке у вiдповiдностi з результатом роботи можна представити у виглядi:
де смуги, якi входять в суму, знаходяться в нижнiй напiвплощинi. Значення параметру gi, наприклад, для полiнома другого порядку знаходимо шляхом вирiшення системи рiвнянь:
Виконавши операцiю сепарації:
на основi рiвняння (3.24) отримаємо оптимальну передаточну функцiю замкнутої системи: W(p) = 1 - Другий член рiшення представляє передаточну функцiю вiдносної помилки та визначається вiдношенням квадратного кореня з спектральної щiльностi перешкоди до факторизованої спектральної щiльностi суми сигналу та перешкоди.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 216; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.224.30 (0.006 с.) |

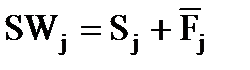 , (3.3)
, (3.3) – довiльний вектор спектральних щiльностей.
– довiльний вектор спектральних щiльностей. , досi невiдомий, може мати особливостi тiльки у правiй на півплощині параметру р.
, досi невiдомий, може мати особливостi тiльки у правiй на півплощині параметру р. включає функцiї, що мають всi полюси та нулi в лiвiй напiвплощинi, а друга матриця
включає функцiї, що мають всi полюси та нулi в лiвiй напiвплощинi, а друга матриця  - в правiй, тобто S =S+ S –
- в правiй, тобто S =S+ S –  =
= 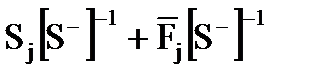 . (3.4)
. (3.4) володiє цiєю властивiстю за визначенням, а S– має нулi та полюси в правiй напiвплощинi. Перший доданок правої частини рiвняння (3.4) включає матрицю
володiє цiєю властивiстю за визначенням, а S– має нулi та полюси в правiй напiвплощинi. Перший доданок правої частини рiвняння (3.4) включає матрицю  , яка мiстить функцiї, що мають полюси як в лiвiй, так i в правiй пiвплощинi.
, яка мiстить функцiї, що мають полюси як в лiвiй, так i в правiй пiвплощинi. , (3.5)
, (3.5) . (3.6)
. (3.6)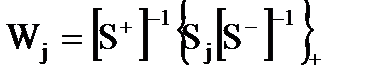 . (3.7)
. (3.7) .
. ST, (3.8)
ST, (3.8)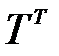 – транспонована матриця ортогональної матрицi Т.
– транспонована матриця ортогональної матрицi Т. , (3.9)
, (3.9) – власнi значення симетричної матрицi S,
– власнi значення симетричної матрицi S, I) Х = 0, (3.10)
I) Х = 0, (3.10) = 0. (3.11)
= 0. (3.11) = 0.
= 0. = 0 (3.12)
= 0 (3.12) . (3.13)
. (3.13) . (3.20)
. (3.20) . (3.21)
. (3.21) . (3.23)
. (3.23) . (3.24)
. (3.24) . (3.25)
. (3.25)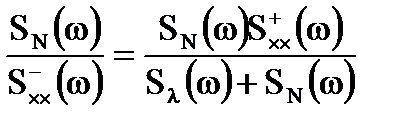 . (3.26)
. (3.26) , (3.27)
, (3.27)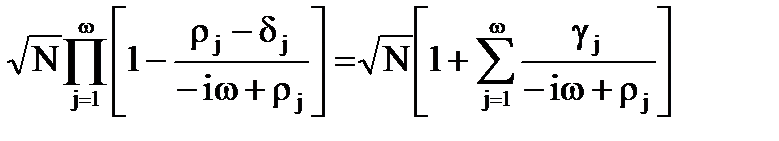 , (3.28)
, (3.28) .
. , (3.29)
, (3.29) . (3.30)
. (3.30)


