
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурний синтез систем довільного порядку.Содержание книги
Поиск на нашем сайте
При відсутності кореляції корисного сигналу і адитивної перешкоди спектральна щільність сумарного вхідного сигналу: Розглянемо найбільш простий випадок, коли корисний сигнал мало змінюється, а перешкода являє собою дельта імпульс, тоді спектральні щільності сигналу описуються швидко спадаючими гіперболічними функціями заданого порядку а завада постійним рівнем сигналу:
Фізична реалізація оптимальної за критерієм мінімуму середньоквадратичної помилки структури системи включає дві додаткові операції - факторизації спектральної щільності вхідного сигналу з шумовою складовою і сепарації відносини спектральних щільностей корисного сигналу і факторизованої спектральної щільності з коренями в правій (нестійкій) півплощині параметра p. Остання операція за рахунок відкидання нестійких складових руху завжди підвищує усталену похибку системи. За рахунок оптимальності перетворення таке підвищення похибки мінімальне. Для виконання операції факторизації необхідно знайти корені поліномів спектральної щільності зашумленого сигналу і розкласти поліном на добуток простих множників, що відповідають лівій (стійкій) півплощині і правій (хитливій) півплощині параметру p. Математичну операцію сепарації виконати складніше. Існує два основних прийоми: розкладання дрібно-раціональної функції відносини спектральних щільностей на суму простих множників та шляхом зворотного перетворення Лапласа з застосуванням теореми Коші про відрахування і пряме перетворення Лапласа сепарованого шляхом інтегрування вираження в півплощині стійких рішень. Для інженерних розрахунків можна використовувати спрощене рішення Ван-Тріса, яке доведене для умов, коли перешкода представлена білим шумом і корені характеристичного поліному відносини спектральних щільностей дійсні. Приклад. Розглянемо структурний синтез системи керування для випадку
де Розкладемо поліном чисельника на прості співмножники, коли 7 коренів розташовані у верхній півплощині
і 7 коренів у нижній півплощині
Таким чином, задача зводиться до знаходження коренів рівняння
Корені з негативною уявною частиною відкидаємо. Тоді порівнюючи (4.40) і (4.39), знаходимо: Таким чином, факторизація спектральної щільності вхідного сигналу дає:
Перейдемо до перемінного p = i
Підставляємо замість a-g їхні числові значення, і, провівши спрощення, одержуємо:
Таким чином, передатна функція замкнутої системи має такий вигляд:
де
Результати розрахунків проведених у відповідності вищеописаним алгоритмом для спектральних щільностей корисного сигналу
Таблиця 4.1. Оптимальні за критерієм СКО структури систем
Продовження таблиці 4.1
Для визначення оптимального закону керування виконана декомпозиція отриманого рішення, шляхом розмикання замкнутої системи автоматичного регулювання, вважаючи уведення негативного одиничного зворотного зв'язку:
Якщо об'єкт управління представлений у виді інтегруючої ланки, то в цьому випадку багатоканальний регулятор має структуру, яка складається з семи паралельних ланок - пропорційної, інтегральної, двох інтегральних і т. ін. до шести послідовно включених інтеграторів або П І І2 І3 І4 І5 І6. Система характеризується астатизмом шостого порядку, коли відсутні похибки за похідною п'ятого порядку або за другою похідною плавності руху. Аналіз формул показує, що відношення постійних часу чисельника до постійної знаменника розімкненої електронної системи завжди більше одиниці. Воно поступово зростає досягаючи значення 6,374. Для випадку коли об¢єкт управління являє собою інтегральну ланку, тоді регулятор можна представити у вигляді паралельного з¢єднання каналів з пропорційною та інтегральними складовими. При збільшенні порядку поліному число таких каналів збільшується пропорційно і кожен складається з послідовного включення інтегральних ланок. Систему керування n-го порядку можна представити такою функціональною схемою, представленою на рис. 3.9. Представимо систем в просторі змінних стану. Для стаціонарної системи відношенню зображень Лапласа вихідного і вхідного сигналів при нульових початкових умовах:
відповідає диференціальне рівняння: any(n)+...+a2y//+ a1ý + a0y = b0x + b1x + b2x// +...+bdxd (4.47) Найбільш поширеним способом представлення передатних функцій систем керувань у просторі змінних стану є таке матричне рівняння: Ý = AY + Bu,
B=[0 0... an-1]T; u 1 =b 0x +b 1x +b2x// +...+bdxd (4.48) Y = [ y 1, y 2 ... yn ] T – стовпець змінних стану системи. Рівнянню (4.48) для передатної функції (4.46) буде відповідати така структура:
Такий спосіб використовують для описання нефорсованих систем керування, коли немає необхідності визначати похідні від вхідних впливів. Ця задача ускладнюється при випадковому характері сигналу. У загальному випадку форсованих систем керування, коли серед коренів є не тільки полюси, але і нулі використовують інший спосіб завдання перемінних стану. Уводиться нова система рівнянь:
(4.49) де Y=[y1, y2,..., yn]т – матриця-стовпець перемінних стану системи; A, B – матриці розмірами (n x n) і (n x 1) відповідно, що характеризують структуру і параметри системи; C-матриця, що відбиває зв'язок перемінних стану Y з вихідним сигналом системи. Оскільки система має один вихід, то C=[100...0]. Матриця стану А відображає динаміку вільної складової стану системи, а матриця В-вплив вхідного сигналу.Порівнюючи системи можна знайти відношення матриці А:
Знайдемо елементи матриці В. Для цього як приклад розпишемо (4.49) для випадку d = n = 2: y = y 1 - ý 1 = y 2 + ý 2 = Підставимо формули (4.51) та (4.50) у вираження (4.52), тоді: y// - y// - a 2 y//+a 1 ý+a 0 y=a 2 Складемо систему рівнянь:
Рішення для випадку n=d=3 дає:
Узагальнюючи (4.54) і (4.55) можна одержати формули для елементів матриці В=[
Представимо систему через рівняння стану: Представимо систему через рівняння стану:
Особливість такого вибору перемінних стану полягає а відсутності необхідності обчислення похідних вхідного сигналу для форсованих систем, що істотно спрощує структуру системи. У цьому випадку можна реалізувати будь-яку систему керування за допомогою набору з інтегральних, пропорційних ланок і суматорів.
Контрольні запитання
1. Що таке фільтр? Для чого він потрібен? 2. Для чого потрібен зворотній зв’язок у системі фільтрації? 3. Що таке перешкода, чи завжди вона присутня у системах обробки інформації? 4. В чому полягає методика Ван-Тріса? 5. Кореляція між сигналом та перешкодою.Її значення. 6. Що таке АКФ? 7. Що дозволяє зробити пряме та зворотнє перетворення Фур’є, Лапласа? 8. Фізичний зміст спектральної щільності сигналу. 9. Для чого необхідний перехід від параметру р до ω? 10. Від чого залежить передатна функція системи? 11. Що собою уявляє система фільтрації n-го порядку? 12. Призначення операцій факторизації та сепарації. 13. Охарактеризувати основні статистичні характеристики сигналів. 14. Представити графічно стаціонарний та нестаціонарний процес. 15. Для чого необхіний зворотній зв’язок у системах керування. 16. На що впливає порядок фільтра? 17. Від чого залежить якість системи керування? 18. В чому відмінність формул Ван-Тріса та Віннера-Хопфа?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.009 с.) |

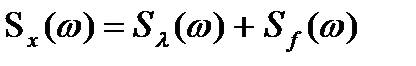 , де
, де 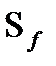 – спектральна щільність завади.
– спектральна щільність завади. . (4.37)
. (4.37) . Спектральна щільність сумарного (шумового) вхідного сигналу:
. Спектральна щільність сумарного (шумового) вхідного сигналу: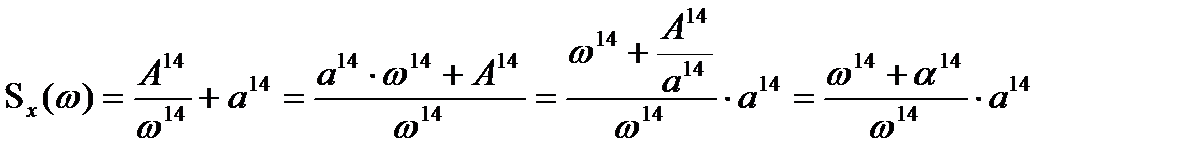 , (4.38)
, (4.38)
 (4.39)
(4.39) (4.40)
(4.40) (тобто чисел a, b, c, d, e, f, g). Вирішуючи цю задачу в середовищі математичних обчислень MATHCAD 2000 PROFESSIONAL /1/ (поставивши курсор у поле рівняння
(тобто чисел a, b, c, d, e, f, g). Вирішуючи цю задачу в середовищі математичних обчислень MATHCAD 2000 PROFESSIONAL /1/ (поставивши курсор у поле рівняння 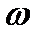 » і вибравши пункт меню Символіка | Перемінні | Дозволити), одержуємо наступні корені:
» і вибравши пункт меню Символіка | Перемінні | Дозволити), одержуємо наступні корені:

 ;
;  ;
;  ;
; 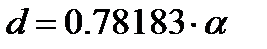 ;
;  ;
;  ;
;  .
.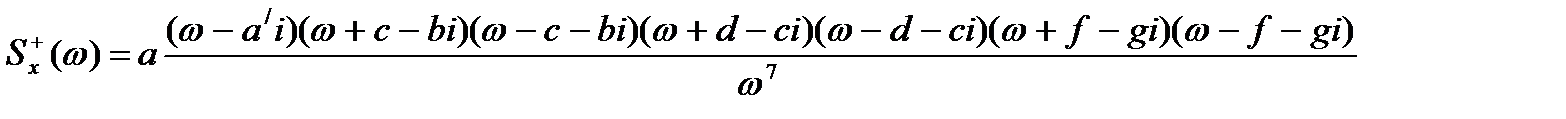 (4.41)
(4.41)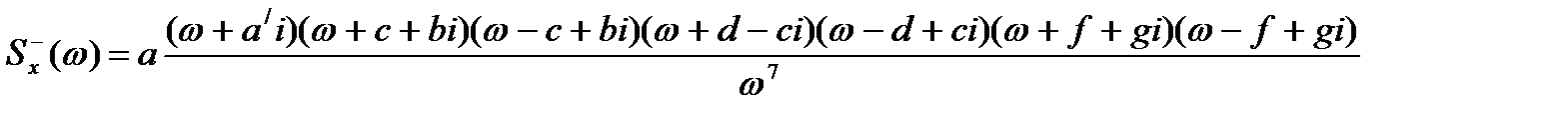 (4.42)
(4.42) (4.43)
(4.43)
 ,
, ;
;  ;
;  ;
; ;
;  ;
;  ;
;  .
. , де n=1,2,3,4,5,6,9 і 11 та відносного рівня завади
, де n=1,2,3,4,5,6,9 і 11 та відносного рівня завади 

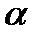


 /
/ 
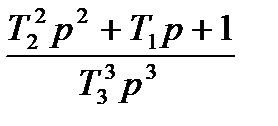









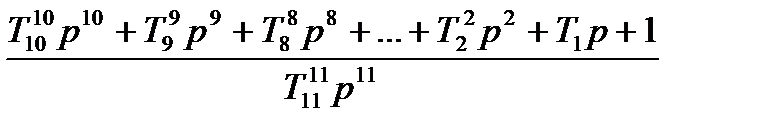
 (4.44)
(4.44)
 (4.45)
(4.45) ,
,  (4.46)
(4.46) ;
;  ;
; 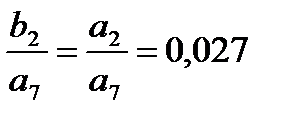 ;
;  ;
; ;
; 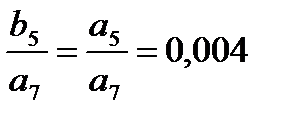 ;
;  .
. 0x
0x

 x = y1 +
x = y1 + 


 x; y = y 1 -
x; y = y 1 -  x; y 2 = ý 1 -
x; y 2 = ý 1 -  -
-  y 1 -
y 1 -  y 2 +
y 2 + 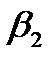 x; (4.52)
x; (4.52)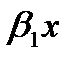 =
= 

 (a 1
(a 1  + a 0
+ a 0 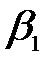 ,
,  ,…,
,…,  ] для будь-якого n (якщо d<n, то просто деякі b виявляться рівними нулю):
] для будь-якого n (якщо d<n, то просто деякі b виявляться рівними нулю):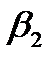 -an-2
-an-2 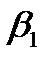 -an- 3 b0)/an
-an- 3 b0)/an

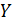 =
=



