
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Стохастичний синтез форсованих систем другого порядкуСодержание книги
Поиск на нашем сайте
Розглянемо суму спектральної щільності випадкового сигналу з періодичною складовою та перешкоди – білого шуму. Поширені дві апроксимації спектральної щільності корисного сигналу – диференцьованою і недиференцьованою функціями. Для першої апроксимації маємо:
Оскільки для спектральної щільності сигналу використовується відношення резонансної частоти до параметру затухання як ступінь регулярності сигналу, то логічно ввести аналогічну характеристику для полінома чисельника сумарного сигналу. Дрібно-раціональна функція має вигляд:
Невідомі параметри знайдемо із системи рівнянь:
Рішення системи рівнянь можна представити в тригонометричній і алгебраїчній формах. В тригонометричній формі невідомі параметри – параметр затухання і ступінь регулярності полінома чисельника сумарного сигналу дорівнюють:
В алгебраїчній формі вони дорівнюють:
Легко показати, що одержані - алгебраїчна та тригонометрична форми запису є еквівалентні. Якщо рівень перешкоди дуже малий, то ступінь регулярності наближається до одиниці. Коли рівень перешкоди дуже великий, тоді параметр затухання сумарного сигналу співпадає з параметром затухання сигналу, як і резонансні частоти, а ступінь регулярності чисельника сумарного сигналу дорівнює ступіню регулярності корисного сигналу. Таким чином, при малому рівні перешкоди ступінь регулярності чисельника сумарного сигналу не залежить від ступіня регулярності корисного сигналу і відношення середньоквадратичних відхилень сигналу і перешкоди і близьке до одиниці. З підвищенням рівня перешкоди ступінь регулярності чисельника сумарного сигналу наближається до ступеня регулярності корисного. Якщо корисний сигнал з періодичною складовою апроксимовано більш простою недиференцьованою функцією, тоді сумарний сигнал має вигляд:
Невідомі параметри знайдемо із системи рівнянь:
Звідки знайшли параметри сумарного сигналу. Параметр затухання:
Ступінь регулярності дорівнює:
Для великого рівня перешкоди залежності ступенів регулярності корисного сигналу і чисельника сумарно одинакові для недиференційної і диференційної апроксимацій сигналу. Але для малого рівня перешкоди для недиференційної апроксимації сигналу ступінь регулярності чисельника сумарного сигналу дорівнює 0,408 для нульового рівня ступеня регулярності сигналу і відповідно одиниці для рівня сигналу, рівного безкінечності. Вказані криві мають спільну точку, коли ступіні регулярності однакові для недиференційної апроксимації і дорівнюють 0,46, а для диференційної апроксимації відповідно одиниці. Для других відношень середньоквадратичних відхилень сигналу і перешкоди криві знаходяться в заштрихованих секторах з тими же точками однакового рівня ступіней регулярності. Оскільки вхідний сигнал може бути добутком більш простих, розглянемо найбільш поширені випадки. При переході від змінної р до змінної ω ліва та права напівплощини переходять відповідно в верхню та нижню напівплощини комплексної площини ω. Дійсно, в наслідок зміни р на іω, одержали:
При переході від якої-небудь точки площини р до відповідної точки площини ω треба повернути радіус-вектор, проведений в площині р, до цієї точки на 90˚ по годнниковій стрільці. Наприклад, спектральна щільність сумарного корисного диференцьованого випадкового сигналу і перешкоди має вигляд:
Корені верхньої напівплощини параметру ω мають вигляд Якщо сумарний сигнал записати в плошині р, тоді:
Корені, які знаходяться в лівій напівплощині параметру р, дорівнюють Перехід від якої-небудь точки площини ω до відповідної точки площини р означає поворот радіуса-вектора, проведеного до цієї точки, на 90˚ проти годинникової стрілки, оскільки із відомої формули:
при ωτ=π/2, можна записати, що
Приклад. Розглянемо задачу оптимальної фiльтрацiї, коли на входi випадковий корисний сигнал має перiодичну складову i апроксимований диференцiйною або недиференцiйною функцiями, а перешкода - бiлим шумом. Спектральну щiльнiсть суми корисного сигналу i перешкоди в загальному виглядi представимо так:
де полiноми чисельника i знаменника являють собою добуток чотирьох спiвмножникiв, якi мають дiйсну частину – параметр затухання корисного або сумарного сигналу i уявну частину - резонансну частоту як добуток ступеня регулярностi на параметр затухання корисного i сумарного сигналiв. Розглянемо спектральну щiльнiсть, апроксимовану диферен цiйною функцiєю. Виконаємо структурний синтез за методикою Ван-Трiса, а для порівняння за методикою виконанням операцiї сепарацiї по теоремi Кошi про лишки (див. додаток 1 приклад 6.1). Методика Ван-Трiса. Виконаємо операцiю факторизацiї, коли комплексно спряженi функцiї, всi нулi та полюси яких знаходяться вiдповiдно в верхнiй та нижнiй напiвплощинах параметра частоти, дорiвнюють:
Оптимальна передаточна функцiя дорiвнює:
Пiсля перетворень одержали передатну функцію форсованої ланки другого порядку:
дe K – коефiцiєнт передачi; Т,Т 1– постiйнi часу; ξ – вiдносний коефiцiєнт затухання. Постiйна часу знаменника дорiвнює:
де μ – параметр затухання корисного сигналу; ψ – cтупiнь регулярностi корисного сигналу; α – вiдношення середньоквадратичних вiдхилень сигналу i перешкоди. Чим бiльше ступiнь регулярностi корисного сигналу, тим менше згаданий добуток, що тим сильнiше, чим бiльше вiдношення параметрiв сигналу i перешкоди. Вiдносний коефiцiєнт затухання:
Для дуже малого вiдносного рiвня перешкоди вiдносний коефiцiєнт затухання не залежить вiд ступеня регулярностi корисного сигналу i наближається до постiйного значення 0,707. Для дуже великого рiвня перешкоди формула для оцiнки добутку постiйної часу на параметр затухання спiвпадає з вiдносним коефiцiєнтом затухання:
Вiдносний коефiцiєнт затухання завжди менше одиницi, для одиничного ступеня регулярностi корисного сигналу дорiвнює 0,707 незалежно вiд корисного сигналу i перешкоди. Для ступеня регулярностi в межах вiд нуля до одиницi вiдносний коефiцiєнт затухання знаходиться в межах вiд 0,707 до одиницi. Коефiцiєнт передачi системи дорiвнює:
Чим бiльше ступiнь регулярностi корисного сигналу, тим менше значення коефiцiєнту передачi. Для дуже малого рiвня перешкоди коефiцiєнт передачi дорiвнює одиницi i не залежить вiд ступеня регулярностi. При дуже великому рiвнi перешкоди коефiцiєнт передачi зменшується до нуля. Постiйна часу форсування:
Добуток постiйної часу на параметр затухання корисного сигналу зменшується з ростом ступеня регулярностi i збiльшенням рiвня перешкоди. Коли вiдносний рiвень перешкоди дуже малий, указаний добуток не залежить вiд ступеня регулярностi i дорiвнює 0,5. Для поширених в техніці спектральних щiльностей корисних сигналів без періодичної складової та з періодичною складовою, яка описується диференційною і недиференційною функціями, а також більш складних моделей та перешкоди в виді білого шуму виконали оптимальний синтез перешкодостійких систем. Повні і неповні поліноми характеристичних рівнянь сигналу мають порядок два, чотири, шість, що відповідає такій же кількості полюсів, причому в двох останніх випадках можуть включати дві пари комплексно-спряжених, характеризуючих коливальні процеси (приклади стохастичного синтезу наведені в додатку 1).
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.209.89 (0.009 с.) |


 (4.18)
(4.18)
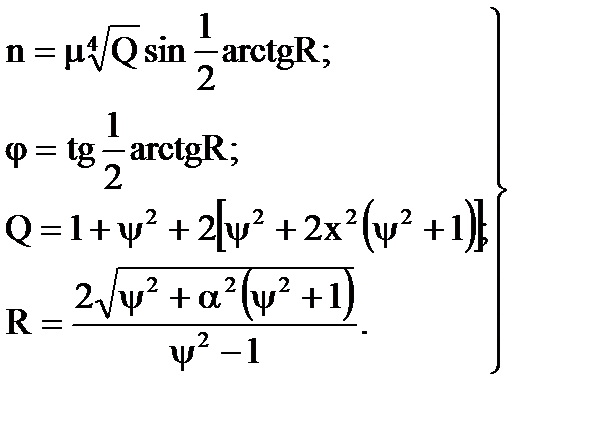 (4.19)
(4.19) (4.20)
(4.20)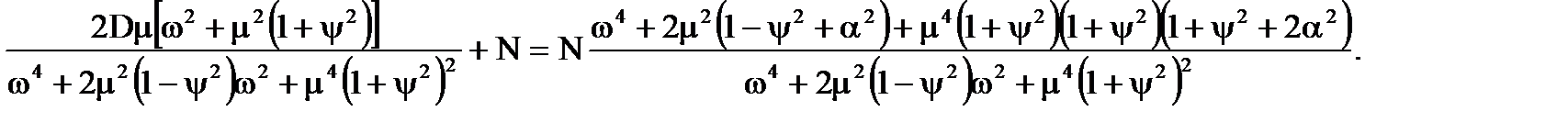

 (4.21)
(4.21) (4.22)
(4.22)
 (4.23)
(4.23) (4.24)
(4.24) і нижньої
і нижньої  (для знаменника) та
(для знаменника) та  і
і  (для чисельника).
(для чисельника). (4.25)
(4.25) для знаменника і
для знаменника і 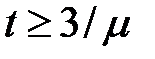 для чисельника, а в правій напівплощині відповідно
для чисельника, а в правій напівплощині відповідно  і
і  .
. . (4.26)
. (4.26) , тому
, тому  .
. ,
,

 , (4.27)
, (4.27) , (4.28)
, (4.28) . (4.29)
. (4.29) .
. . (4.30)
. (4.30) . (4.31)
. (4.31)


