Вплив періоду дискретизації на динаміку

Електронної системи

 

Цифровий фільтр (ЦФ) – пристрій, проникний або пригнічуючий задані в цифровій формі сигнали в певній смузі частот.

На відміну від аналогових фільтрів, де вхідний сигнал змінюється безперервно, в цифрових фільтрах вхідний сигнал представляється в дискретній формі, тобто приймає нове значення через інтервал дискретизації. Величина зворотна цьому інтервалу – частота дискретизації, - в більшості практичних випадків повинна перевищувати смугу частот вхідного сигналу в 4...8 раз. Дискретні сигнали природно виникають в тих випадках, коли джерело повідомлень видає інформацію у фіксовані моменти часу. Наприклад, пристрій вимірювання температури, пов'язаний з міським світловим табло, посилає сигнал на це табло в певні проміжки часу. В інших проміжках на табло висвічуються тиск, час або інші параметри. Тут яскраво виявляється характер дискретного сигналу: в паузах немає ніяких відомостей про зміну температури. Таким чином, ми маємо справу не з безперервною зміною температури, а лише з її значеннями, відліченими через певні проміжки часу. Подібний процес називається дискретизацією безперервного сигналу.

Властивість дискретного сигналу – існувати лише в певні проміжки часу – дозволяє організувати передачу по одній і тій же лінії (радіоканалу, парі дротів, оптичному волокну) повідомлень від декількох різних джерел. Дискретні сигнали можна задавати графіками, як це показано на мал. 9.15, формулами, наприклад i_д(t)= sin (2p f nT), у вигляді таблиць дискретних значень або у вигляді комбінації цих способів.

Рисунок 9.15. Варианти графічного завдання сигналу.

 

Перевага ЦФ перед аналоговими:

Цифрові фільтри (ЦФ) в порівнянні з аналоговими мають такі переваги.

1. ЦФ можна виконати в мікроелектронному виконанні, наприклад у вигляді одної інтегральної схеми.

2. Якщо для обробки сигналів в реальному масштабі часу використовується цифрова ЕОМ тоді ЦФ можна запрограмувати на цій же машині.

3. ЦФ мають високу завадостійкість, зв¢язану з використанням цифрових схем.

4. Висока точність ЦФ визначається похибкою округлення при арифметичних операціях в ЕОМ, а точність в аналогових схемах залежить від допусків на елементи схем і перешкод.

5. Зміна характеристик ЦФ можлива шляхом зміни програми або її частини, параметри можна змінити шляхом зміни коефіцієнтів різницевого рівняння.

6. Напруга живлення, коливання температури, старіння елементів змінюють характеристики аналогових фільтрів, але не впливають на програми які знаходяться в ЕОМ, так як характеристики фільтрів залишаються постійними.

· Висока стабільність характеристик

· Простота перебудови частотної характеристики

· Можливість в одному пристрої виконати відразу дещо ЦФ

Переваги ЦФ особливо помітні в діапазоні низьких та інфранизьких частот особливо при біомедичних дослідженнях. Низькочастотні, високочастотні, полосові та загороджуючі фільтри можуть бути створені комбінацією двох фільтрів низької частоти та всечастотного. Математичні моделі фільтрів діляться на дві великі групи БІХ і КІХ фільтри.

КІХ фільтри мають кінцеве число ненульових значень імпульсної характеристики, це може бути лише тоді, коли всі коефіцієнти А дорівнюють нулю. Прикладами КІХ фільтрів являються просте та зважене середнє, де для усереднення не використовується експоненційне середнє не враховуються властивості електронної системи.

БІХ фільтри мають нескінчене число ненульових значень імпульсної характеристики, і діляться на дві групи нефорсованих і форсованих фільтрів. В першому випадку враховуються насамперед властивості електронної схеми і важливими являються показники не тільки стійкості фільтра але і показники якості перехідних процесів, особливо при підвищенні порядку рівняння. Моделі таких БІХ фільтрів розраховують за відомими методиками: Баттерворта, Чебишева і Бесселя. Друга група БІХ фільтрів представляє собою форсовані еліптичні фільтри являється комбінацією двох вище згаданих. Перетворення вхідного сигналу, як в КІХ фільтрах прискорює процеси обчислень і не впливає на стійкість, але впливає на показники якості перехідних процесів, але врахування властивостей електронної схеми (як експоненційне середнє) уповільнює процеси обчислень і впливає як на стійкість так і показники якості перехідних процесів.

При розгляді дискретних сигналів необхідно зрозуміти суть теореми Котельникова. В 1933 році в роботі “Про пропускну спроможність “ефіру” і дроту в електрозв'язку” В.А. Котельников довів теорему, що стала основоположному в теорії і техніці цифровому зв'язку. Вона свідчить: якщо безперервний сигнал x(t) має спектр, обмежений частотою F_ГР, то він може бути повністю і однозначно відновлений по його дискретних відліках, узятих через інтервали часу T=1/2F_ГР, тобто з частотою f _д =2F_гр.

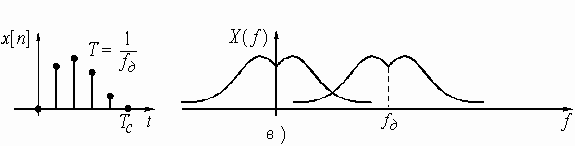
Рисунок 9.16. Накладення сигналів і спектрів.

Справедливість теореми легко побачити з рис. 9.16 в) і 9.16 а). Частота дискретизації безперервного сигналу не повинна бути менше подвоєної ширини спектру: f_д≥2F_гр інакше відбудеться накладення спектрів (рис. 9.16. б) і буде неможливо за допомогою фільтру нижніх частот виділити спектр початкового безперервного сигналу.

Способи реалізації ЦФ діляться на тимчасові і частотні. До тимчасових відносяться ЦФ з кінцевою імпульсною характеристикою (КІХ-фільтри) і з нескінченною імпульсною характеристикою (БІХ-фільтри). В таких ЦФ синусоїдальний сигнал, частота якого розташовується в смузі частот ЦФ, поданий на вхід ЦФ у вигляді дискретних відліків, зберігає свою синусоїдальну форму. До частотних способів реалізації ЦФ відносяться фільтри з дискретним перетворенням Фурье (ДПФ) і швидким перетворенням Фурье (БПФ). В таких ЦФ при подачі на вхід синусоїдального сигналу на одному з виходів спостерігатиметься сигнал постійного рівня, тобто такі ЦФ здійснюють одночасно і детектування сигналу.

КІХ-фільтри мають полюси (коріння знаменника) рівні нулю і характеризуються кінцевою імпульсною характеристикою. КІХ-фільтри можуть мати більш різноманітні АЧХ, ніж БІХ-фільтри. Важливою особливістю КІХ-фільтрів є те, що фазова характеристика може бути строго лінійна j(w) = - const w. Якщо ця умова виконана, то імпульсна характеристика фільтру володіє властивістю симетрії.

Якщо на вхід БІХ-фільтру подати відлік одиничної амплітуди, то вихідні відліки формуватимуться як сума затриманих відліків з різними терезами а1, а2.., які знову через суматор подаються на пристрій затримки. Процес може тривати нескінченно, звідки і назва фільтру.

Для більшості практичних випадків основною характеристикою будь-якого фільтру є його частотна характеристика. Перетворення Фурье від частотної характеристики називається імпульсною характеристикою фільтру.