Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розв’язок систем нелінійних рівнянь
Постановка задачі Багато практичних задач зводиться до розв’язку систем нелінійних рівнянь. На відміну від систем лінійних рівнянь, не існує прямих методів розв’язку нелінійних систем. Загальний метод розв’язку системи рівнянь має складатися з двох етапів: відділення коренів і подальшого уточнення розв’язку. Для одержання розв’язку звичайно використовуються ітераційні методи. Вибір первинних наближень впливає на збіг ітераційного процесу; вони мають бути досить близькими до точного розв’язку. У протилежному випадку ітераційний процес може не збігтися. Первинне наближення знаходять графічно (для випадку двох рівнянь із двома невідомими) або іншими методами (аналітичними, методом проб) для систем з великою кількістю рівнянь. Розглянемо систему нелінійних рівнянь:
У матричному виді:
де
Метод Ньютона і методи простої ітерації та Зейделя є ітераційними методами. Метод Ньютона має велику швидкість збігу. У той же час метод простої ітерації має більш прості умови збіжності і є менш критичним до вибору первинного наближення. Тому для високоточних обчислень рекомендується застосовувати спочатку метод простої ітерації. Після того, як знайдені наближення, досить близькі до точних, використовувати метод Ньютона. Числові методи розв’язку Метод Ньютона
Якщо знайдені
де Розкладаючи ліву частину
у ряд Тейлора, обмежуючись лінійними членами розкладання, одержуємо систему лінійних рівнянь відносно виправлень:
Розв’язувати отриману систему лінійних рівнянь можна будь-яким методом з розглянутих в розділі 1. При розв’язанні системи методом зворотної матриці отримаємо рекурентну формулу для обчислення виправлень, а звідси і формулу ітераційного процесу визначення розв’язку системи (2.1) або (2.2), яка отримала назву методу Ньютона:
де
Якщо в формулі (2.5) матрицю, зворотну до матриці Якобі, обчислювати на кожній ітерації в фіксованій початковій точці
Процес ітерації (2.5) триває доти, поки не буде справедлива нерівність:
де Зауваження Метод Ньютона ефективний тільки при достатній близькості первинного наближення до розв’язку системи. Вимоги до збіжності методу досить жорсткі, теореми про швидкість збіжності, стійкість наведені у [7]. Практично метод Ньютона застосовується для уточнення розв’язку, отриманого яким-небудь іншим методом. Матриця Якобі містить частинні похідні першого порядку. Оскільки аналітичне диференціювання в загальних випадках небажано, окремі похідні заміняють їх наближеними кінцево-різницевими значеннями:
Метод простої ітерації
Для розв’язку системи нелінійних рівнянь методом простої ітерації необхідно навести її у виді:
Ітераційний процес реалізується наступними формулами:
Ітераційний процес продовжується доки не буде досягнуте виконання умов (2.11) або (2.12): · критерій з абсолютних відхилень:
· критерій з відносних відхилень (якщо
де Умова збіжності методу визначається формулою
де
матриця частинних похідних правих частин Метод Зейделя
Метод Зейделя є модифікованим методом простої ітерації, на відміну від якого, уточнені значення коренів відразу підставляються в наступні рівняння. Послідовні наближення визначаються із співвідношень:
Все сказане відносно збіжності методу простої ітерації в п. 2.2.2, вірно і для методу Зейделя, тобто умова збіжності залишається такою самою.
Завдання
Розв’язати систему нелінійних рівнянь з точністю до 1) За методом Ньютона отримати систему лінійних рівнянь та розв’язати ії прямим методом з завдання 1.5 п. 1); 2) Розв’язати систему ітераційним методом (ітерацій або Зейделя). Метод вказано в таблиці варіантів; 3) Порівняти результати, отримані за пп. 1) і 2); 4) Навести блок-схеми алгоритмів використаних методів.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.200.86 (0.009 с.) |
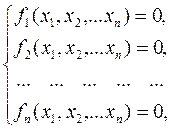 (2.1)
(2.1) (2.2)
(2.2) ,
,  (2.3)
(2.3) -і наближення до розв’язку
-і наближення до розв’язку  , можна записати точний розв’язок
, можна записати точний розв’язок  системи (2.1) у виді:
системи (2.1) у виді: ,
,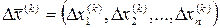 – виправлення до розв’язку, що шукається.
– виправлення до розв’язку, що шукається. (2.4)
(2.4) .
. (2.5)
(2.5) , (2.6)
, (2.6)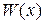 – матриця Якобі,
– матриця Якобі, – матриця, зворотна до матриці Якобі.
– матриця, зворотна до матриці Якобі. замість
замість  (тобто використовуємо зафіксовану зворотну матрицю), отримаємо модифікований метод Ньютона. Очевидно, цей метод вимагає менше обчислень, але й дає меншу точність.
(тобто використовуємо зафіксовану зворотну матрицю), отримаємо модифікований метод Ньютона. Очевидно, цей метод вимагає менше обчислень, але й дає меншу точність. (2.7)
(2.7)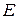 – необхідна точність,
– необхідна точність, , (2.8)
, (2.8) .
. (2.9)
(2.9)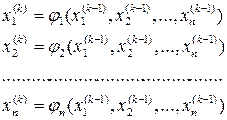 (2.10)
(2.10) (2.11)
(2.11) ):
): (2.12)
(2.12) , (2.13)
, (2.13) ,
,  – перша або друга норма матриці
– перша або друга норма матриці 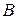 ,
, (2.14)
(2.14) ,
,  , системи (2.9), обчислених у точці первинного наближення
, системи (2.9), обчислених у точці первинного наближення  ,
,  , …,
, …,  .
. (2.15)
(2.15) .
.