
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Канонічні рівняння методу силСодержание книги Поиск на нашем сайте
Додаткові рівняння переміщень, що виражають рівність нулю переміщень (лінійних чи кутових) у напрямках зайвих невідомих, зручно складати в так званій канонічній формі, тобто за певною закономірністю.
Обчислюючи де
Якщо
Це канонічна форма рівняння переміщень для один раз статично невизначуваної системи. Для системи з двома зайвими зв’язками додаткові рівняння мають вигляд: Виходячи з принципу незалежності дії сил, запишемо переміщення
За аналогією можна записати в канонічній формі рівняння переміщень для будь-якої n разів статично невизначуваної системи:
Повне переміщення
Система канонічних рівнянь методу сил для загального випадку навантаження має вигляд:
де Коефіцієнти Коефіцієнти і вільні члени канонічних рівнянь (2.6) обчислюються за допомогою інтегралу Мора, що представляється в загальному випадку формулою[1].
де складання проводиться по усім дільницям пружної системи. В прийнятій системі координат (вісь При застосуванні графоаналітичних методів для визначення інтегралів Мора (2.7) необхідно мати відповідні епюри від одиничних навантажень Епюри Для багатопрольотної балки відмінними від нуля внутрішніми зусиллями вважати згинальний момент та поперечну силу. Для плоскої рами - згинальний момент, поперечну і поздовжню сили. Згідно з п.1.1, на підставі формули (2.7) знаходимо
Питомі переміщення, що мають однакові індекси й називаються головними коефіцієнтами канонічних рівнянь, визначають таким чином
Очевидно, що ці переміщення додатні. Питомі переміщення, в яких індекси не однакові, називають побічними коефіцієнтами й визначають за формулою
Вони можуть бути додатними або від’ємними, а також дорівнювати нулю. На підставі теореми про взаємність переміщень Плоскопросторові рами являють собою особливий клас стержньових конструкцій, у яких плоска рамна система навантажена силами, діючими в площинах, не співпадаючих з площиною самої рами
Очевидно, що при дії сил, перпендикулярних площині рами (рис. 18), відмінними від нуля внутрішніми зусиллями в перерізі рами є
Якщо ж площина дії зовнішніх сил співпадає з площиною рами, відмінними від нуля є
Оскільки будь-яке зовнішнє навантаження можна розкласти на дві складові, одна з яких розміщена в площині рами Таким чином, система канонічних рівнянь (2.6) для плоскопросторової рами в загальному випадку розпадається на дві незалежні системи:
Де
В випадку, якщо зовнішнє навантаження є антиплоским Отже, для плоскопросторових рам, навантажених ортогонально до її площини, ступінь статичної невизначуваності
Значення коефіцієнтів канонічних рівнянь, як показують вирази (2.7), залежать від співвідношення згинальних Якщо рама зібрана з прямолінійних стержнів постійної згинальної і крутної жорсткості, то безпосереднє інтегрування в формулі Мора можна замінити перемноженням епюр по способу Верещагіна (1.8).
|
|||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.105.184 (0.007 с.) |


 (рис.17б), прирівняємо до нуля повне переміщення точки В основної системи в напрямі
(рис.17б), прирівняємо до нуля повне переміщення точки В основної системи в напрямі 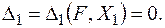 (2.1)
(2.1) , застосуємо принцип незалежності дії сил:
, застосуємо принцип незалежності дії сил: 
 – переміщення від заданого навантаження (рис. 17в);
– переміщення від заданого навантаження (рис. 17в); – переміщення від сили
– переміщення від сили  – переміщення в напрямі
– переміщення в напрямі  (рис.17г), то
(рис.17г), то  , і рівняння переміщень (2.1) набирає вигляду:
, і рівняння переміщень (2.1) набирає вигляду: (2.2)
(2.2) де
де  – повне переміщення в напрямі
– повне переміщення в напрямі  ;
;  – повне переміщення в напрямі
– повне переміщення в напрямі  у вигляді сум переміщень, спричинених окремо кожною з невідомих сил
у вигляді сум переміщень, спричинених окремо кожною з невідомих сил 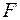 . Використовуючи вибрані раніше позначення переміщень, знаходимо:
. Використовуючи вибрані раніше позначення переміщень, знаходимо: (2.3)
(2.3) (2.4)
(2.4) можна визначити як добуток питомого переміщення
можна визначити як добуток питомого переміщення  , спричиненого дією одиничної сили, на відповідну узагальнену силу –
, спричиненого дією одиничної сили, на відповідну узагальнену силу – 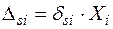 .
.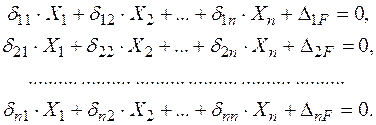 (2.5)
(2.5) (2.6)
(2.6) – кількість зайвих зв'язків (ступінь статичної невизначуваності) системи.
– кількість зайвих зв'язків (ступінь статичної невизначуваності) системи.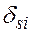 рівнянь (2.6) являють собою лінійні зміщення та кути повороту в основній (статично визначуваній) системі від дії сил і моментів
рівнянь (2.6) являють собою лінійні зміщення та кути повороту в основній (статично визначуваній) системі від дії сил і моментів  , доданих по напрямкам
, доданих по напрямкам 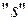 невідомих зусиль. Вільні члени
невідомих зусиль. Вільні члени  визначають відповідні переміщення, викликані заданим зовнішнім навантаженням.
визначають відповідні переміщення, викликані заданим зовнішнім навантаженням. (2.7)
(2.7) співпадає з віссю стержня, а
співпадає з віссю стержня, а  і
і  – головні центральні осі поперечного перерізу) крутний момент
– головні центральні осі поперечного перерізу) крутний момент  і згинальні моменти
і згинальні моменти 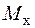 і
і  , поздовжня
, поздовжня 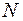 та поперечні сили
та поперечні сили 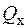 і
і 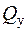 є сукупністю проекцій головного вектору і головного моменту сил в довільному перерізі стержня.
є сукупністю проекцій головного вектору і головного моменту сил в довільному перерізі стержня. , які будують для основної системи навантаженою тільки силами
, які будують для основної системи навантаженою тільки силами  кожною окремо.
кожною окремо. , будують також для основної системи, але від заданого зовнішнього навантаження. Ординати епюр згинальних моментів відкладають з боку стислого волокна.
, будують також для основної системи, але від заданого зовнішнього навантаження. Ординати епюр згинальних моментів відкладають з боку стислого волокна. (2.8)
(2.8)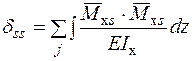 (2.9)
(2.9) (2.10)
(2.10)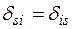 [1].
[1]. .
.

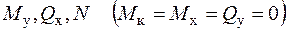
 , а інша – в перпендикулярній площині
, а інша – в перпендикулярній площині  , ці невідомі поділяються на дві самостійні групи і можуть бути визначені незалежно друг від друга.
, ці невідомі поділяються на дві самостійні групи і можуть бути визначені незалежно друг від друга. (2.11)
(2.11) – невідомі зусилля і моменти, діючі в площинах, ортогональних до площини рами;
– невідомі зусилля і моменти, діючі в площинах, ортогональних до площини рами; – невідомі і моменти, що лежать в площині рами.
– невідомі і моменти, що лежать в площині рами. ,
, 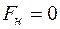 , вільні члени
, вільні члени  системи (2.11) звертаються в нуль, що призводить до нульових рішень для зусиль
системи (2.11) звертаються в нуль, що призводить до нульових рішень для зусиль  визначається числом додаткових зв'язків, накладених на раму в площині дії зовнішнього навантаження. Відмінними від нуля невідомими
визначається числом додаткових зв'язків, накладених на раму в площині дії зовнішнього навантаження. Відмінними від нуля невідомими  (2.12)
(2.12) ,
,  та крутної
та крутної  жорсткостей поперечних перерізів стержньової системи та довжин
жорсткостей поперечних перерізів стержньової системи та довжин  відповідних ділянок стержня.
відповідних ділянок стержня.


