
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклади визначення переміщень.Содержание книги Поиск на нашем сайте Приклад 1.
Допоміжну систему навантажуємо одиничною силою у точці А, де треба визначити переміщення і визначаємо опорні реакції
Записуємо рівняння згинальних моментів від зовнішніх навантажень
Формуємо інтеграл Максвелла – Мора і визначаємо переміщення в перерізі А.
- Для визначення прогину в перерізі А за допомогою графоаналітичних методів необхідно мати епюри згинального моменту від зовнішнього
Додатне значення прогину
Приклад 2.
Допоміжну систему навантажуємо одиничним моментом в перерізі А, де треба визначити кутове переміщення і визначаємо опорні реакції
Записуємо рівняння згинальних моментів від зовнішніх навантажень
Формуємо інтеграл Мора і визначаємо кутове переміщення в перерізі А.
- Для визначення кутового переміщення в перерізі А за допомогою графоаналітичних методів необхідно мати епюри згинального моменту від зовнішнього
Негативне значення кута повороту Приклад 3.
Визначаємо опорні реакції
Визначення повного переміщення
Записуємо рівняння згинальних моментів від зовнішніх навантажень
Формуємо інтеграл Мора і визначаємо вертикальне переміщення в перерізі А.
- Для визначення вертикального переміщення в перерізі А за допомогою графоаналітичних методів необхідно мати епюри згинального моменту від зовнішнього
Записуємо рівняння згинальних моментів від зовнішніх навантажень
Формуємо інтеграл Мора і визначаємо горизонтальне переміщення в перерізі А.
- Для визначення горизонтального переміщення в перерізі А за допомогою графоаналітичних методів необхідно мати епюри згинального моменту від зовнішнього
Вектор повного переміщення
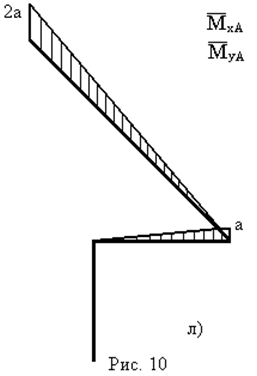
Приклад 4. Для консольної просторової рами (рис. 10а) навантаженої розподільним навантаженням
Дано:
У випадку консольної просторової рами, навантаженої зовнішніми зусиллями на одній чи кількох ділянках, вирази для внутрішніх силових факторів, а також і епюри цих внутрішніх силових факторів можна записати без визначення опорних реакцій. При цьому перерізи для визначення виразів внутрішніх зусиль треба вибирати починаючи з вільного кінця рами і далі до місця закріплення. Для просторової рами визначення переміщення складається з визначення переміщень в напрямку кожної осі (
1. Визначення переміщення
- Запишемо вирази для згинальних і крутних моментів
- Запишемо вирази для згинальних і крутних моментів
Формуємо інтеграл Мора і визначаємо
Визначення переміщення
2. Визначення переміщення
- Запишемо вирази для згинальних і крутних моментів
- Запишемо вирази для згинальних і крутних моментів
Формуємо інтеграл Мора і визначаємо
Визначення переміщення
3. Визначення переміщення
- Запишемо вирази для згинальних і крутних моментів
- Запишемо вирази для згинальних і крутних моментів
Формуємо інтеграл Мора і визначаємо
Визначення переміщення
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 319; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |


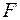 та розподільним навантаженням
та розподільним навантаженням  на ділянці довжиною
на ділянці довжиною  визначити лінійне вертикальне переміщення перерізу
визначити лінійне вертикальне переміщення перерізу  -
-  .
Дано:
.
Дано: 


 .
Визначаємо опорні реакції
.
Визначаємо опорні реакції  для навантаження зовнішніми
зусиллями (рис. 7а).
для навантаження зовнішніми
зусиллями (рис. 7а).

 .
. (рис. 7б).
(рис. 7б).

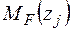 і одиничного навантаження
і одиничного навантаження  на ділянках балки.
на ділянках балки.


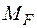 (рис. 7в) та одиничного
(рис. 7в) та одиничного  (рис. 7г) навантажень. На ділянці, де
(рис. 7г) навантажень. На ділянці, де 
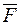 .
.
 та силою
та силою  .
Дано:
.
Дано: 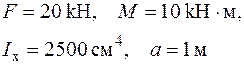 Визначаємо опорні реакції
Визначаємо опорні реакції  для навантаження зовнішніми зусиллями (рис. 8а).
для навантаження зовнішніми зусиллями (рис. 8а).

 (рис.8б).
(рис.8б).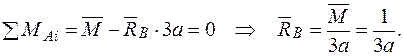








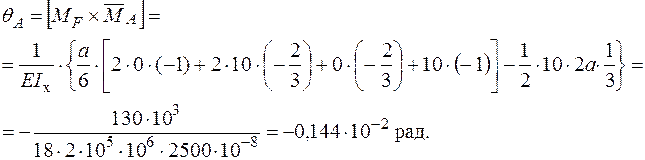
 , тобто в напрямку обертання часової стрілки.
, тобто в напрямку обертання часової стрілки.
 і
і  , визначити повне лінійне переміщення в точці
, визначити повне лінійне переміщення в точці  .
Дано:
.
Дано: 
 при навантаженні рами зовнішніми зусиллями (рис. 9а).
при навантаженні рами зовнішніми зусиллями (рис. 9а).


 та горизонтального
та горизонтального  переміщень.
переміщень.




 і одиничного навантаження
і одиничного навантаження  на ділянках балки.
на ділянках балки.




 (рис. 9г) навантажень.
(рис. 9г) навантажень.





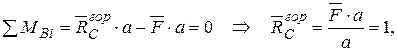

 і одиничного навантаження
і одиничного навантаження  на ділянках балки.
на ділянках балки.




 (рис. 9е) навантажень.
(рис. 9е) навантажень.



 визначити повне лінійне переміщення перерізу А -
визначити повне лінійне переміщення перерізу А - 



 - в напрямку осі
- в напрямку осі  ;
;  ;
;  - в напрямку осі
- в напрямку осі  ).
).
 – від зовнішніх навантажень
– від зовнішніх навантажень


 – від одиничного навантаження.
– від одиничного навантаження.
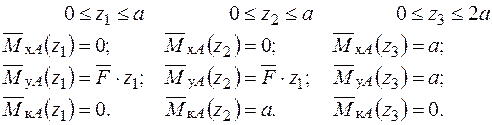



 – від зовнішніх навантажень (рис. 10б,в) і
– від зовнішніх навантажень (рис. 10б,в) і  – від одиничного навантаження (рис. 10д,е).
– від одиничного навантаження (рис. 10д,е).

 – від зовнішніх навантажень:
– від зовнішніх навантажень:
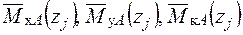 – від одиничного навантаження:
– від одиничного навантаження:






 – від зовнішніх навантажень (рис. 10б,в) і
– від зовнішніх навантажень (рис. 10б,в) і  – від одиничного навантаження (рис. 10з,и).
– від одиничного навантаження (рис. 10з,и).


 – від одиничного навантаження:
– від одиничного навантаження:

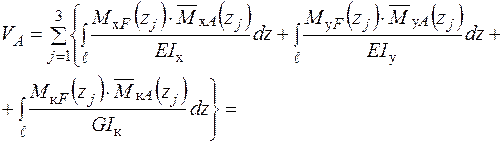


 – від одиничного навантаження (рис. 10л,м).
– від одиничного навантаження (рис. 10л,м).
 (рис.11) і має відповідну довжину:
(рис.11) і має відповідну довжину:





