Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Енергетичні методи визначення переміщень в стержньових системахСодержание книги
Поиск на нашем сайте
Інтеграл Максвелла – Мора Розглянемо довільну плоску стержньову систему (балку, раму, ферму), навантажену заданими зовнішніми силами
Застосуємо початок можливих переміщень для допоміжного стану, ввівши як можливі дійсні переміщення заданої системи [1]:
де Вираз (1.1) є загальною формулою для пружного переміщення плоскої стержньової системи. Якщо виходити з виразу початку можливих переміщень [1], то у загальному випадку просторової стержньової системи при довільному навантаженні загальна формула для визначення пружного переміщення містить шість додатків і її можна записати і вигляді:
Індекси “x”, “y” в формулі (1.2) позначають головні осі перерізу ділянки стержня, індекс “к” – крутний момент. Зазначимо, що наведені формули можна застосовувати і для криволінійних стержнів малої кривизни. Формули (1.1) та (1.2) вперше були виведені Максвеллом (для поздовжніх переміщень) і Мором. Визначення переміщень за цими формулами часто називають методом Максвелла – Мора. Зазначимо, що метод Максвелла – Мора – це найзагальніший метод визначення переміщень стержньових систем. Здебільшого при визначенні переміщень у балках, рамах та криволінійних брусах можна знехтувати впливом поздовжніх деформацій і деформацій зсуву, враховуючи лише переміщення, спричинені згинанням і крученням. При цьому для балок та плоских рам впливом поперечних та поздовжніх сил, як правило, нехтують і враховують лише згинальні моменти Тоді формула (1.1) для плоскої системі набирає вигляду
і називається інтегралом Мора. При просторовому навантажуванні, згідно з формулою (1.2),
При визначенні переміщень вузлів шарнірних ферм, що складаються з прямих стержнів, які працюють лише на розтягання – стискання у формулі Мора зберігається тільки один додаток:
Ця формула має назву формули Максвелла. Можна запропонувати таку послідовність визначення переміщень за допомогою інтеграла Максвелла – Мора: Будують допоміжну систему, яку навантажують одиничним навантаженням у точці, де треба визначити переміщення і в напрямку, в якому треба визначити переміщення. Визначаючи лінійні переміщення, у заданому напрямі прикладають одиничну силу, визначаючи кутові переміщення, - одиничний момент. Для кожної ділянки системи записують вирази силових факторів у довільному перерізі заданої Обчислюють інтеграли Максвелла - Мора (по ділянках в межах всієї системи). Як вже зазначалося, при розрахунку плоских балок, рам і арок виходять з формули (1.3), просторових систем – (1.4), ферм – (1.5). Якщо обчислене переміщення позитивне, то це означає, що його напрям збувається з вибраним напрямом одиничної сили. Негативний знак свідчить про те, що дійсний напрям переміщення, що визначається, протилежний напряму одиничної сили.
1.2 Обчислення інтегралів Мора способом перемноження епюр (способом Верещагіна). Обчислення інтегралів Мора істотно спрощується, якщо одна з епюр прямолінійна. Ця умова виконується для систем, що складаються з прямих стержнів, оскільки при цьому епюри внутрішніх сил від одиничного навантаження (зосередженої сили або пари) завжди обмежені прямими лініями. Обчислимо інтеграл
Інтеграл у правій частині рівняння є статичним моментом площі епюри
де Тоді Отже, інтеграл Мора дорівнює добутку площі епюри від зовнішнього навантаження
Графоаналітичний спосіб визначення інтеграла Мора був запропонований О.М.Верещагіним і має назву способу Верещагіна. Обчислення за цією формулою виконують по ділянках, на кожній з яких епюра від одиничного навантаження повинна бути прямолінійною. Тоді, коли обидві епюри прямолінійні, можна множити площу будь-якої з них на ординату іншої під центром ваги першої. Якщо епюра Отже,
Користуючись способом Верещагіна, необхідно пам'ятати, що добуток епюр позитивний, якщо ординати обох епюр відкладені з одного боку від осі стержня рами, і негативний, якщо ординати епюр відкладені з різних сторін. В тих випадках, коли одна з епюр криволінійна, береться площа
Рис. 3 Переміщення від дії осьових і поперечних сил, а також крутних моментів виражаються аналогічно:
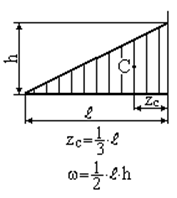
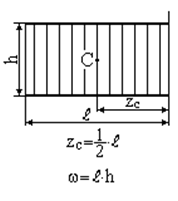
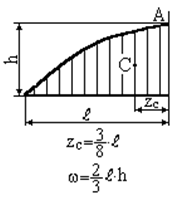
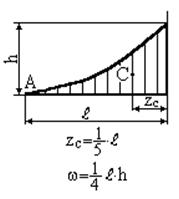
де Зазначимо, що епюри внутрішніх силових факторів від зовнішнього та одиничного навантажень на окремих ділянках стержня складаються з досить простих фігур: прямокутник, трикутник, парабола і т.д. Тоді для використання способу Верещагіна (1.8), (1.9) необхідно визначити площу Таблиця 1
Продовження таблиці 1
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 238; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.250.115 (0.006 с.) |

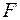 (рис. 1а).
(рис. 1а).
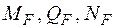 . Визначимо переміщення (узагальнене)
. Визначимо переміщення (узагальнене) 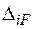 будь-якої точки системи в напрямі m-m. Введемо допоміжний стан (рис. 1б), що є заданою системою, навантаженою лише однією одиничною силою (узагальненою)
будь-якої точки системи в напрямі m-m. Введемо допоміжний стан (рис. 1б), що є заданою системою, навантаженою лише однією одиничною силою (узагальненою) 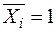 , прикладеною в тій самій точці і в напрямі шуканого переміщення
, прикладеною в тій самій точці і в напрямі шуканого переміщення 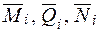 .
.
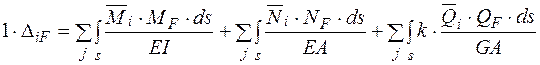 (1.1)
(1.1) – кількість ділянок розрахункової схеми, k – коефіцієнт форми перерізу.
– кількість ділянок розрахункової схеми, k – коефіцієнт форми перерізу.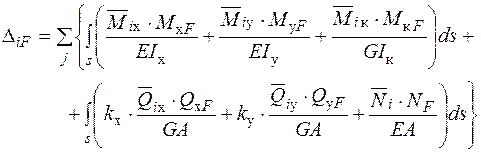 (1.2)
(1.2)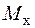 . Однак, визначаючи переміщення в балках, для яких відношення висоти перерізу до довжини прольоту
. Однак, визначаючи переміщення в балках, для яких відношення висоти перерізу до довжини прольоту 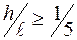 поперечні сили враховувати обов’язково. При визначенні переміщень в рамах з великими зазначеними відношеннями
поперечні сили враховувати обов’язково. При визначенні переміщень в рамах з великими зазначеними відношеннями  похибка, спричинена неврахуванням інтегралів поздовжніх та поперечних сил, також може стати істотною. Слід мати на увазі, що в реальних балочних та рамних конструкціях величина відношення
похибка, спричинена неврахуванням інтегралів поздовжніх та поперечних сил, також може стати істотною. Слід мати на увазі, що в реальних балочних та рамних конструкціях величина відношення 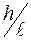 , як правило, менше за
, як правило, менше за 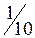 . Тому при обчисленні переміщень у загальній формулі Максвелла – Мора цілком допустимо зберегти інтеграл, що враховує лише згинальні моменти [1].
. Тому при обчисленні переміщень у загальній формулі Максвелла – Мора цілком допустимо зберегти інтеграл, що враховує лише згинальні моменти [1].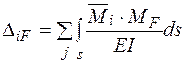 , (1.3)
, (1.3) (1.4)
(1.4)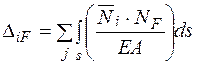 (1.5)
(1.5)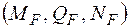 і допоміжної
і допоміжної  систем.
систем.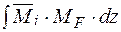 для випадку, коли
для випадку, коли 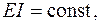 епюра від заданого навантаження має довільну форму, а від одиничного – прямолінійна (рис. 2).
епюра від заданого навантаження має довільну форму, а від одиничного – прямолінійна (рис. 2).
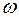 площу епюри
площу епюри 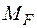 , С – її центр ваги,
, С – її центр ваги,  – ординату епюри від одиничного навантаження під центром ваги епюри
– ординату епюри від одиничного навантаження під центром ваги епюри  є диференціалом площі епюри
є диференціалом площі епюри  . Тоді шуканий інтеграл
. Тоді шуканий інтеграл
 (1.6)
(1.6)

 – абсциса центра ваги епюри
– абсциса центра ваги епюри 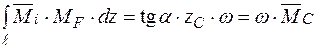 , оскільки
, оскільки 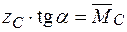 .
. (1.7)
(1.7)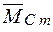 літерами
літерами 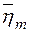 , де
, де  .
.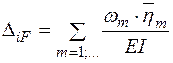 (1.8)
(1.8)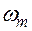 криволінійної епюри, а ордината
криволінійної епюри, а ордината 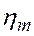 під центром ваги з прямолінійної епюри. При цьому треба враховувати правило знаків: Якщо епюри, що перемножуються, лежать по одну сторону (обидві нагорі або внизу), добуток позитивний; якщо епюри, що перемножуються, лежать по різні сторони - добуток негативний. Якщо одна або обидві епюри перетинають в межах дільниці нульову ось, то слідує перемножувати епюри по частинам. Особливості застосування правила Верещагіна видно з рис. 3а,б.
під центром ваги з прямолінійної епюри. При цьому треба враховувати правило знаків: Якщо епюри, що перемножуються, лежать по одну сторону (обидві нагорі або внизу), добуток позитивний; якщо епюри, що перемножуються, лежать по різні сторони - добуток негативний. Якщо одна або обидві епюри перетинають в межах дільниці нульову ось, то слідує перемножувати епюри по частинам. Особливості застосування правила Верещагіна видно з рис. 3а,б.
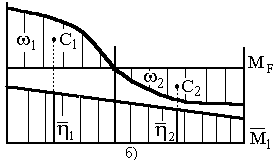

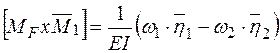
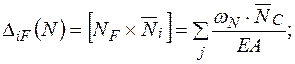
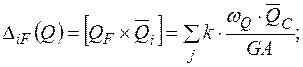 (1.9)
(1.9)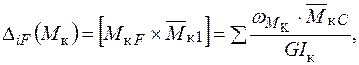
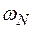 - площа епюри
- площа епюри  ,
, 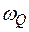 - площа епюри
- площа епюри 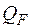 ,
, 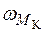 - площа епюри
- площа епюри 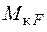 від заданого навантаження;
від заданого навантаження;  - ординати відповідних епюр осьових, поперечних сил і крутних моментів від одиничного навантаження, взяті під центрами ваги епюр
- ординати відповідних епюр осьових, поперечних сил і крутних моментів від одиничного навантаження, взяті під центрами ваги епюр