
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однорідні рівняння. Рівняння, які зводяться до однорідних.Содержание книги
Поиск на нашем сайте
Д.Р. називається однорідним, якщо його можна подати у вигляді:
Воно за допомогою заміни змінної y/x=u Þy=ux зводиться до Д.Р. з відокремлюваними змінними.
та знаходження розв’язку зводиться до квадратур:
Тригонометричні рівняння, які не є однорідні, легко зводяться до однорідних. Наприклад, якщо в рівнянні sin х cos x = 0,5 представить 0,5 в виде 0,5 (sin2 х + cos2 х), то получится однородное уравнение
65. Лінійні диференціальні рівняння. Рівняння Бернуллі.
Озн. Р-ння виду
__________ Метод Бернуллі
Метод полягає у тому, що розв’язуючи рівняння (1) шукають у вигляді: деякі ф-ції від х, при чому одна з них довільна і
_____
_________ Рівняння Бернуллі
Якщо n=0, то ми одержали лінійне рівняння Якщо n=1 р-ня з розподілними змінними.
Рівняння Бернуллі завжди має розв*зок у=0
Змінна частина
Зауваження 1)Р-ння Бернуллі може бути розв*язано безпосередньо методом Бернуллі. 2)
66. Рівняння в повних диференціалах. Інтегруючий множник.
Озн. Р-ння виду P(x;y)dx+Q(x;y)dy=0 (1), де P(x;y) i Q(x;y) – деякі неперервні в деякій області D ф-ції. Назив. р-ням у повних диференціалах, якщо його ліва частина є повним диференціалом деякої ф-ції U(x;y).
Отже, р-ня (1) зводиться до вирішування ф-ції U du=0 U=C – загальн. розв. ____ Одержане рівняння продиферненц. Спочатку по х, потім по у і одержимо:
Озн. Ф-ція Загального методу знаходження Якщо 67. Диференціальні рівняння вищих порядків. Загальний i частинний розв'язки. Теорема Koшi.
Озн. Диф рів-ня n-того порядку назив. р-ння виду F(x;y
Озн. Нормальним або явним диф. рівнянням n-того порядку назив. р-ння виду:
Озн. Розв*язком р-ння 2 на деякому інтервалі (а;b) назив. n раз неперервно-диференційовна на цьому інтервалі ф-ція
Заг.розв*язком р-ня (2) назив. ф-ція y=
Озн. Частинним розв*язком р-ння (2) назив. ф-ція Де
В задачах, яких необхідно знайти частинний розв*язок диф. рів-ня (2), що задовольняє поч.умови (3) назив. задачею Коші.
Існування і єдність розв*язку задачі Коші визнач. Теоремою.
Якщо в деякому околі т.(
68. Диференціальні рівняння, які допускають зниження порядку Уравнения, допускающие понижение порядка Уравнение где x - независимая переменная, y - искомая функция, а функция F определена и непрерывна в некоторой области Рассмотрим некоторые типы уравнений высших порядков, допускающие понижение порядка. Уравнения, не содержащие искомой функции и нескольких последовательных производных. Рассмотрим уравнения вида С помощью замены
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 719; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.36 (0.006 с.) |




 (1) назив. лнійним неоднорідним р-ням І-ого порядку, де Р(х) і f(x) деякі задані на проміжку неперервні ф-ції.
(1) назив. лнійним неоднорідним р-ням І-ого порядку, де Р(х) і f(x) деякі задані на проміжку неперервні ф-ції. - наз. однорідним рівнянням.
- наз. однорідним рівнянням.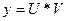 , де U=U(x) V=V(x)
, де U=U(x) V=V(x)



 - рівняння такого виду називається р-ням Бернуллі.
- рівняння такого виду називається р-ням Бернуллі.


 , така заміна зводить рівняння до лінійного.
, така заміна зводить рівняння до лінійного.
 , то крім розв*язку y=U*V
, то крім розв*язку y=U*V  тотож.)
тотож.)
 (х;у)
(х;у)  .
. )=0 (1) x- незалежна змінна, у=у(х)
)=0 (1) x- незалежна змінна, у=у(х) (x;y
(x;y  ) (2).
) (2). , яка при підстановці в дане р-ння перетворює його в тотожність, для будь-якого Х з інтервала (а;b).
, яка при підстановці в дане р-ння перетворює його в тотожність, для будь-якого Х з інтервала (а;b). =
= 
 , яка містить стільки довільних незалежних сталих, яким є порядок рівняння і яка задовольняє цьому рівнянні при довільних значеннях
, яка містить стільки довільних незалежних сталих, яким є порядок рівняння і яка задовольняє цьому рівнянні при довільних значеннях  , де і=
, де і= 
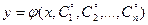 , яку одержують із загального розв*язку, якщо кожній довільній сталій
, яку одержують із загального розв*язку, якщо кожній довільній сталій  надати конкретного числового значення. Для цього задають n початкових умов
надати конкретного числового значення. Для цього задають n початкових умов  (3),
(3), - довільна наперед задані дійсні числа.
- довільна наперед задані дійсні числа. (4)
(4) ) ф-ція
) ф-ція  визначена, неперервна і має неперервні частинні похідні по аргументам
визначена, неперервна і має неперервні частинні похідні по аргументам  і т.д., то існує такий окіл цієї точки в якому задача Коші(4) має розв*язок і при тому єдиний. Для диф. р-ння ІІ порядку геометр. зміст полягає у тому, що через задану точку, в заданому напрямі проходить лише одна крива, через цю точку можуть проходить і інші криві, але з іншим нахилом дотичної.
і т.д., то існує такий окіл цієї точки в якому задача Коші(4) має розв*язок і при тому єдиний. Для диф. р-ння ІІ порядку геометр. зміст полягає у тому, що через задану точку, в заданому напрямі проходить лише одна крива, через цю точку можуть проходить і інші криві, але з іншим нахилом дотичної. , (1)
, (1) и во всяком случае зависит от
и во всяком случае зависит от  , называется обыкновенным дифференциальным уравнением n -го порядка.
, называется обыкновенным дифференциальным уравнением n -го порядка. . (2)
. (2) , где u - новая неизвестная функция, уравнение (2) приводится к уравнению (n-k) -го порядка:
, где u - новая неизвестная функция, уравнение (2) приводится к уравнению (n-k) -го порядка: .
.


