
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функція багатьох змінних. Означення та символіка. Границя функції. Графік функціїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Мета заняття Формування первинних уявлень про функцію двох (трьох) змінних та її графік, умінь знаходити області визначення та множину значень функції двох змінних. Розвивати логічне мислення, допитливість.
Студенти повинні знати: означення функції багатьох змінних; поняття області визначення та множини значень функції; поняття графіка функції двох та трьох змінних; та символіку теми. Студенти повинні вміти: відрізняти функції багатьох змінних, знаходити та зображувати області визначення та множини значень функцій двох та трьох змінних; Основні питання теми До теперішнього часу ми розглядали та вивчали функцію однієї змінної х. Але в природі існує багато процесів і залежностей, коли, щоб отримати результати того чи іншого процесу, необхідно мати дані двох, трьох або більше параметрів. Отже, існують функції, які залежать від двох або більше змінних. 1.Означення функції двох змінних; приклади; 2.Область визначення та множина значень; 3.Межа області визначення; відкриті та замкнені області; приклади; 4.Графік функції двох змінних; лінії рівня; 5.Границя функції багатьох змінних; 6.Неперервність функції багатьох змінних; 7.Приклади
Завдання для самоперевірки 1.Знайти область визначення D функції z = 2.Дослідити на неперервність функції а) z = 2х2 + 3у; б) z = (х + у – 1)/(у2 – 2х). 3.Знайти та зобразити області визначення функцій двох змінних: 1. 3. 5. 7. 9. 11. 13. Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 гл.6, стор. 284 – 294. Лекція „Означення функції багатьох змінних” Означення. Якщо кожній точці множини D n -вимірного простору Rn за деяким законом Р (х 1, х 2, …, хn) поставлено у відповідність одне і тільки одне дійсне число
При цьому D називають областю визначення функції, а Е — областю значень функції. Згідно з означенням функцію Зокрема, коли n = 2, маємо функцію двох змінних Зауважимо, що в задачах економічного змісту найчастіше доводиться стикатися з функціями двох або трьох незалежних змінних. Тому надалі головну увагу приділятимемо саме їм.
Наведемо приклади таких функцій.
Криву, що являє собою множину точок, кожною з яких подається одна з можливих комбінацій двох факторів виробництва, котрі забезпечують однакову кількість виготовлюваної продукції, зображено на рис. 1.
Рис. 1.
Нехай предметами споживання є два товари А — масло та В — маргарин, ціни на які становлять відповідно р 1 та р 2. Якщо ціни на інші товари сталі, а прибуток споживачів і структура споживання не змінюються, то попит і пропозиція за кожним із товарів залежать від його ціни. Маємо: функцію попиту на товар А: q 1 = f 1(p 1, p 2); функцію попиту на товар В: q 2 = f 2(p 1, p 2); функцію пропозиції товару А: s 1 = f 3(p 1, p 2); функцію пропозиції товару В: s 2 = f 4(p 1, p 2). Задану умовою задачі залежність можна подати такою таблицею:
Попит на масло визначатиметься функцією Зокрема, ця функція може набирати такого вигляду:
або Способи задання функції Функцію двох змінних, як і функцію однієї змінної, можна подати такими способами: · аналітично (у вигляді формули); наприклад:
· таблично; наприклад:
(таблиця множення чисел: z = xy) · графічно (рис. 2);
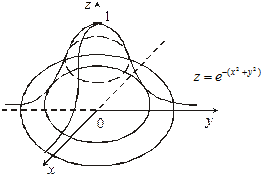
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 574; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.115.79 (0.01 с.) |

 + ln(4 – х2 – у2)
+ ln(4 – х2 – у2) . 2.
. 2.  .
. . 4.
. 4.  .
. . 6.
. 6.  .
. . 8.
. 8.  .
. . 10.
. 10.  .
. . 12.
. 12. 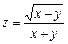 .
. . 14.
. 14.  .
. , то говорять, що в області
, то говорять, що в області  задано функцію n незалежних змінних.
задано функцію n незалежних змінних.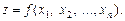
 можна розглядати як функцію точки і записувати як
можна розглядати як функцію точки і записувати як 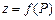 .
. , якщо кожній парі
, якщо кожній парі  на площині поставлено у відповідність одне і тільки одне число z.
на площині поставлено у відповідність одне і тільки одне число z. Витрати виробництва даного виробу за даної технології є функцією матеріальних витрат х і витрат у на оплату робочої сили:
Витрати виробництва даного виробу за даної технології є функцією матеріальних витрат х і витрат у на оплату робочої сили:  ,
, 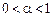 ;
;  , де Q — обсяг виробництва; С — деяка стала; L — кількість праці, яку вкладено у виробництво; K — кількість капіталу. Із наведеної рівності випливає, що частка, %, заробітної плати в загальному прибутку становить a × 100, а частка капіталу, %, b × 100. Задану функцію можна подати у вигляді таблиці або графіка. Для двох факторів таким графіком може бути рівнопродуктова крива, для більшої їх кількості — деякий тривимірний образ.
, де Q — обсяг виробництва; С — деяка стала; L — кількість праці, яку вкладено у виробництво; K — кількість капіталу. Із наведеної рівності випливає, що частка, %, заробітної плати в загальному прибутку становить a × 100, а частка капіталу, %, b × 100. Задану функцію можна подати у вигляді таблиці або графіка. Для двох факторів таким графіком може бути рівнопродуктова крива, для більшої їх кількості — деякий тривимірний образ.
 і залежатиме від його ціни р 1 та ціни р 2 конкурентного товару — маргарину.
і залежатиме від його ціни р 1 та ціни р 2 конкурентного товару — маргарину. ,
, .
. .
.


