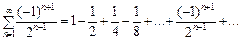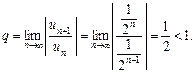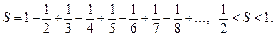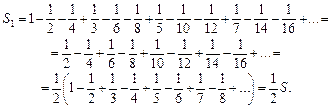Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знакозмінні ряди. Ознака Лейбніца. Абсолютна та умовна збіжності рядівСодержание книги
Поиск на нашем сайте
. Мета заняття Вивчити поняття знакозмінного ряду та ознаку, за якою можна визначити його збіжність. Навчитися визначати абсолютну та умовну збіжно-сті рядів. Розвивати уважність, логічне мислення, вміння виділити головну думку теми
Студенти повинні знати: поняття знакозмінного ряду, його властивості, ознаку Лейбніца; поняття абсолютної та умовної збіжності рядів. Студенти повинні вміти: користуватися різними ознаками при дослідженні рядів на збіжність;досліджувати ряди на абсолютну та умовну збіжность.
Основні питання теми 1.Ряди, в яких знаки членів строго чергуються; 2.Ознака Лейбніца; 3.Знакозмінні ряди; 4.Ознака збіжності знакозмінного ряду; 5.Абсолютно та умовно збіжні ряди; 6.Приклади.
Свої набуті знання ви можете перевірити в наступному тесті 1.Вираз u1 + u2 + u3 +...+ un... називається... а)нескінченною сумою б)скінченною сумою в)рядом г)рівнянням з n-змінними 2.Сума n-перших членів ряда називається... а)загальною сумою ряда б)вибірковою сумою ряда в)інтегральною сумою ряда г)частинною сумою ряда 3.Якщо послідовність частинних сум ряда збіжна і ця границя дорівнює S, то це число S називається... а)сумою ряда б)збіжністю ряда в)розбіжністю ряда г)загальним членом ряда 4.Якщо ряд має кінцеву суму, то він називається... а)розбіжним б)збіжним в)сумованим г)кінцевим 5.Якщо послідовність частинних сум ряду не має скінченної границі, то ряд називається... а)розбіжним б)збіжним в)сумованим г)кінцевим 6.На збіжність ряду не впливає.. а)зміна знаків усіх членів б)відкидання від нього скінченної кількості членів ряду в)додавання до нього скінченної кількості членів ряду г)обертання усіх членів ряду 7.Якщо ряд збіжний, то границя його загального члена... а)не існує б)дорівнює `+` нескінченності в)дорівнює `-` нескінченності г)дорівнює `0` 8.Якщо границя загального члена ряда не дорівнює 0, то ряд буде.. а)розбіжним б)збіжним в)гармонійним г)загальним 9.Ряд, довільні два сусідні члени якого мають різні знаки, називається рядом, члени якого... а)строго додатні б)строго від`ємні в)строго чергуються г)знакозмінні 10.Якщо серед членів ряда є як від`ємні, так і додатні, то ряд називається... а)збіжним б)розбіжним в)строго змінним г)знакозмінним 11.Якщо ряд, утворений з модулів членів ряду, є збіжним, то сам знакозмінний ряд називається.... а)абсолютно збіжним б)умовно збіжним в)незбіжним г)розбіжним 12.Якщо знакозмінний ряд є збіжним, а ряд, утворений з модулів його членів, розбіжний, то даний ряд називається... а)абсолютно збіжним б)умовно збіжним в)незбіжним г)розбіжним
Завдання для самоперевірки Дослідити на збіжність ряди 1. 5. 9. 11. 13. 15. Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл. 9, стор. 505 – 509. Лекція „Збіжність рядів зі знакозмінними членами” Знакопочергові ряди. Ознака збіжності Лейбніца Означення. Ряд виду
де аn > 0 (n = 1, 2, 3, …), називається знакопочерговим рядом.
Лейбніц указав достатню умову збіжності ряду (1). Теорема 1. Нехай у знакопочерговому ряді (1) послідовність аn (n = 1, 2, 3, …) монотонно спадає. Якщо
ряд (1) збігається і його сума не перевищує а 1.
Усі умови теореми 1 виконані, і тому ряд збігається. Абсолютна й умовна збіжність Розглянемо довільний числовий ряд
Означення. Ряд (2) називається абсолютно збіжним, якщо збігається ряд
Збіжний ряд (2) називається умовно збіжним, якщо ряд (3) розбіжний.
Очевидно, що із збіжності ряду (3) випливає збіжність ряду (2), бо члени ряду (22) можуть мати різні знаки. Теорема 2. Абсолютно збіжний ряд збігається. Оскільки для рядів з додатними членами відомі достатні ознаки збіжності, то їх можна використовувати для дослідження збіжності рядів за знакопочерговими членами. Теорема 3. Якщо для знакопочергового ряду
Існують границі
Дослідимо збіжність ряду
●Знаходимо границю
Отже, ряд, що розглядається, збігається абсолютно. Раніше відмічалося, що в довільному ряді не можна переставляти члени ряду. Наведемо без доведення такі твердження. Теорема 4. Якщо ряд збігається абсолютно, то за будь-якої перестановки членів ряд буде збігатися і сума його не змінюватиметься. Теорема 5. (Теорема Рімана.) Якщо ряд збігається умовно і s — будь-яке наперед задане число, то завжди можна переставити члени ряду так, щоб сума отриманого ряду дорівнювала s. Дамо пояснення до теореми Рімана. Умовна збіжність ряду виконується завдяки тому, що додатні і від’ємні члени взаємно знищуються. Якщо скласти ряд лише із додатних членів і ряд лише із від’ємних членів, то ці ряди розбігаються. Отже, можна почергово обирати лише додатні або від’ємні числа так, щоб значення частинних сум було як можна ближче до значення s. При цьому сума ряду дорівнюватиме s.
Переставимо члени ряду так, щоб після додатного члена стояли два від’ємні. При цьому дістанемо ряд
За такого переставлення членів ряду сума ряду зменшилась удвічі. Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл. 9, стор. 505 – 509. Тема 24
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 770; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.239.189 (0.006 с.) |

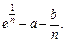 2.
2. 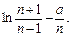 3.
3. 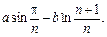 4.
4. 
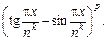 6.
6. 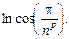 7.
7. 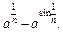 8.
8. 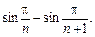
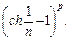 10.
10. 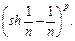
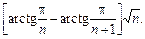 12.
12. 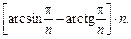
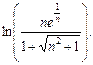 14.
14. 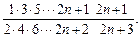
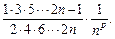
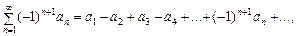 (1)
(1)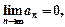
 Дослідимо збіжність знакопочергового ряду
Дослідимо збіжність знакопочергового ряду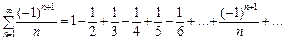
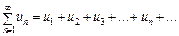 (2)
(2)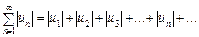 (3)
(3)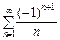 є умовно збіжним, бо ряд
є умовно збіжним, бо ряд 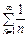 розбіжний.
розбіжний.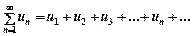
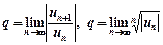 ,
,