
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Роз'вязування систем лінійних рівнянь за формулами КрамераСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Мета теми: навчитися розв'язувати системи лінійних рівнянь за допомогою формул Крамера Студент повинен знати: означення визначника третього та n порядків, властивості; теорему про розкладання визначника. Формули Крамера для систем 2-х,3-х лінійних рівнянь з 2-ма,3-ма змінними; кількість розв'язків системи залежно від значень визначників системи. Студент повинен вміти:обчислювати визначники другого, третього та четвертого порядків; застосовувати теорему про розкладання визначника за елементами рядків та стовпчиків для обчислювання визначників. Застосовувати формули Крамера для розв'язування систем лінійних рівнянь
Основні питання теми: 1.Означення визначника 2, 3 та n порядку. 2.Загальний вигляд визначника n порядку. 3.Властивості визначників. 4.Формули Крамера для систем двох лінійних рівнянь. 5.Формули Крамера для систем трьох лінійних рівнянь. 6.Умови існування розв'язків системи. 7.Приклади розв'язання систем.
Свої набуті знання ви можете перевірити за наступними питаннями 1.Який вигляд має система 2-х, 3-х лінійних рівнянь з двома, трьома змінними? 2.Що таке головний визначник системи? 3.Який вигляд мають формули Крамера? 4.Коли система має єдиний розв'язок? 5.Коли система має безліч розв'язків? 6.Коли система не має розв'язків? 7.Чи можна застосовувати формули Крамера для будь-якої системи лінійних рівнянь?
Завдання для самоперевірки Розв’язати за формулами Крамера системи рівнянь
Відповідь.
Відповідь.
Відповідь.
Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001, стор.21 – 23.
Лекція ” Формули Крамера” Спинимося на застосуванні теорії визначників до розв’язування системи n лінійних алгебраїчних рівнянь з n невідомими:
Означення. Визначник, елементами якого є коефіцієнти при невідомих у системі (1)
називається визначником цієї системи. Теорема. Якщо визначник D системи лінійних алгебраїчних рівнянь (1) відмінний від нуля, то ця система має єдиний розв’язок:
Тут Dk — визначник, утворений з визначника D системи (1) заміною k -го стовпця на стовпець із правих її частин.
Доведення. Помноживши k -те рівняння системи (1) на алгебраїчне доповнення Aks елемента аks і додавши всі рівняння, дістанемо:
Згідно з властивостями 9 і 10 визначників маємо рівняння
з якого при Отже, якщо система рівнянь (1) має розв’язок, то він подається у вигляді (3). Доведемо, що ці формули справді визначають розв’язок системи рівнянь (1), підставивши туди розв’язки (3). Для k -го рівняння маємо:
з якого випливає справедливість теореми. ¨
· Запишемо відповідні визначники і знайдемо розв’язки системи рівнянь:
· Обчислимо визначник цієї системи:
Визначник системи відмінний від нуля. Знайдемо тепер визначник
Формули Крамера незручні для практичних обчислень при Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001
Тема 3: Ранг матриці. Умови сумісності та визначеності СЛР Мета теми: усвоїти поняття ранга матриці; навчитися обчислювати ранг матриці, а також визначати сумісність і визначеність системи лінійних рівнянь. Студент повинен знати: означення матриці; види матриць; поняття мінора та алгебраїчного доповнення до елемента матриці; поняття ранга матриці; умови сумісності та визначенності системи лінійних рівнянь. Студент повинен вміти: виконувати дії над матрицями (додавання, віднімання, множення на число, множення матриць); обчислювати визначники 2-го, 3-го, 4-го порядків; знаходити обернену матрицю; обчислювати мінори та алгебраїчні доповнення до елементів матриці; знаходити ранг матриці.
Основні питання теми: 1.Поняття ранга матриці 2.Обчислення ранга матриці 3.Методи обчислення рангів 4.Умови сумісності та визначенності системи лінійних рівнянь. 7.Приклади обчислення рангів матриць.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 573; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.155.143 (0.008 с.) |

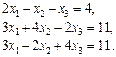

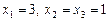 . Відповідь.
. Відповідь.  .
.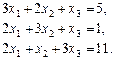
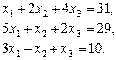
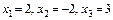 . Відповідь.
. Відповідь.  .
.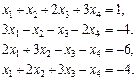
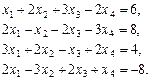

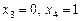 .
.
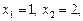
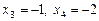 .
.
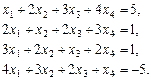
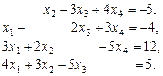

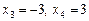 .
.
 .
.
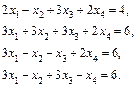


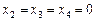 .
.
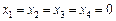 .
.

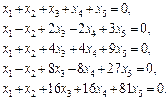

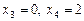 .
.
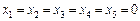 .
.

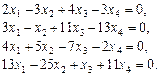
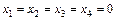 . Відповідь.
. Відповідь. 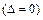 .
.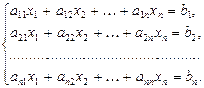 (1)
(1)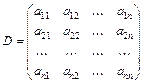 , (2)
, (2)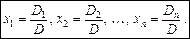 (3)
(3)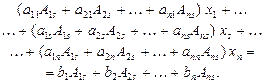
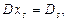
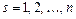 випливають формули (3).
випливають формули (3).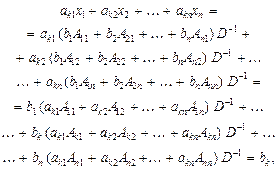
 Розв’яжемо за формулами Крамера систему рівнянь:
Розв’яжемо за формулами Крамера систему рівнянь:


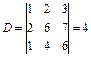 .
. і розв’язки системи рівнянь:
і розв’язки системи рівнянь: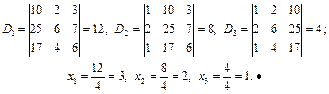
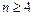 , але вони застосовуються в теоретичних дослідженнях.
, але вони застосовуються в теоретичних дослідженнях.


