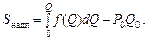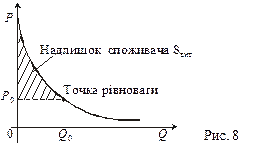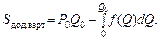Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування визначеного інтегралу до обчислення площ фігур, об’ємів тіл та розв’язування фізичних задачСодержание книги
Поиск на нашем сайте
Мета заняття Набуття вмінь та навичок застосовувати знання про визначений інтеграл до розв’язування задач. Розвивати уважність, зацікавленість, логічне мислення.
Студенти повинні знати: задачі, в яких застосувується визначений інтеграл; формули для обчислення площ фігур, об'ємів тіл обертання, шляху, що пройшла точка, роботи сили, тиску рідини. Студенти повинні вміти: застосовувати інтеграли до обчислювання площ фігур, об'ємів тіл обертання, розв'язувати задачі з фізики за допомогою інтеграла.
Основні питання теми Існує дві основних схеми застосування визначеного інтеграла: так званий метод інтегральних сум та метод диференціала. Сьогодні ми розглянемо застосування визначеного інтеграла до розв’язування геометричних та фізичних задач. 1.Обчислення площ плоских фігур 2.Обчислення шляху, що пройшла точка 3.Обчислення довжини дуги 4.Обчислення об’єма тіла 5.Обчислення роботи сили 6.Обчислення тиску рідини на вертикальну пластину 7.Приклади.
Свої набуті знання ви можете перевірити в наступному тесті 1.Фігура, що обмежена графіком функції у = f(х), прямими х = а, х = b і відрізком [а;b] осі ОХ називається... а)рівнобедреною трапецією б)невизначеною трапецією в)прямокутною трапецією г)криволінійною трапецією 2.Площа криволінійної трапеції на відрізку а;b дорівнює... а)визначеному інтегралу на відрізку а;b б)добутку середньої лінії трапеції a на висоту трапеції b в)(а + b)h г)abR 3.Якщо існує і має кінцеве значення границя інтегральних сум, яка не залежить від розбиття відрізка а;b на частини та від вибору точок на кожному інтервалі, то ця границя називається... а)невизначеним інтегралом б)визначеним інтегралом в)криволінійним інтегралом г)невласним інтегралом 4.Робота А змінної сили F(х), яка діє на відрізку а;b, дорівнює.. а)дотичній до сили б)похідній від сили в)визначеному інтегралу від сили г)невизначеному інтегралу від сили 5.Шлях, пройдений точкою за проміжок часу від t = а до t = b, дорівнює...... а)дотичній до швидкості v(t) б)похідній від швидкості v(t) в)невизначеному інтегралу від швидкості v(t) г)визначеному інтегралу від швидкості v(t) 6.Фізичний зміст визначеного інтеграла - це... а)шлях S, пройдений точкою від t = а до t = b зі швидкістю v(t)
б)площа S криволінійної трапеції в)робота А змінної сили F(х) г)маса m неоднорідного стержня Завдання для самоперевірки 1.Охарактеризувати дві основні схеми застосування визначеного інтеграла до розвязування практичних задач. 2.Обчислити площу фігури, обмеженої прямою у = х і параболою у = 2 – х2 3.Обчислити площу поверхні частини параболоїда, утвореного обертанням навколо осі ОХ параболи у2 = 2х, де 0 ≤ х ≤ 4. 4.За допомогою визначених інтегралів обчислити площі фігур, що обмежені лініями: 1. 5. 8. Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл. 7, стор. 401 – 411.
Для більш глибокого вивчення теми рекомендовано обрати одну із запропонованих тем для написання реферату. Теми рефератів 1.Використання поняття визначеного інтеграла для отримання моделей задач економічного характеру. 2.Історія розвитку інтегрального числення. Лекція „ Застосування визначеного інтеграла”
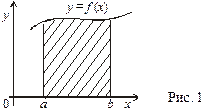
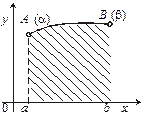
1. Якщо на відрізку [ a, b ] функція f (x) ³ 0, то площа криволінійної трапеції, обмеженої кривою у = f (x), віссю Ох і прямими х = а і х = b, подається так:
Рис. 2
●Знаходимо точки перетину кривих:
отже,
Рис. 3 Звідси за формулою (2)
3. Якщо криву задано рівняннями в параметричній формі
то площа криволінійної фігури обчислюється за формулою
● Cправді, нехай рівняння (3) визначають деяку функцію у = f (x) на відрізку [ a, b ]. Тоді площа криволінійної трапеції може бути обчислена за формулою:
Рис. 4
●За формулою (4) маємо:
1. Довжина дуги кривої у прямокутних координатах. Нехай у прямокутних координатах на площині задано криву рівнянням у = f (x), де f (x) і f ¢(x) — неперервні на відрізку [ a, b ] функції. Знайдемо довжину дуги АВ цієї кривої, що міститься між вертикальними прямими х = a i x = b (рис. 5).
Рис. 5
Нагадаємо означення довжини дуги кривої. Візьмемо на дузі АВ точки А, А 1, А 2, …, В з абсцисами а = x 0, x 1, x 2, …, xn = b і проведемо хорди АА 1, А 1 А 2, …, Аn– 1 B, довжини яких позначимо відповідно D l 1, D l 2, …D ln. Тоді дістанемо ламану АА 1 А 2 … Аn– 1 B, вписану в другу АВ. Довжина ламаної дорівнює
Означення. Довжиною l дуги АВ називається границя, до якої прямує довжина вписаної в цю дугу ламаної, коли довжина її найбільшої ланки прямує до нуля:
Довжина дуги кривої обчислюється за формулою:
●За формулою (6) маємо:
Застосування визначеного інтеграла 1. Загальні витрати споживачів на товар. Розглянемо криву попиту Р = f (Q) на деякий товар (рис. 6). Якщо Р — ціна одиниці товару, то загальна сума витрат на придбання товару Q буде Р × Q.
Рис. 6
На рис. 6 позначено: Р 0 — ціна рівноваги; Q 0 — кількість товару, який продається за ціною Р 0. Припустимо, що товар у кількості Q 0 не відразу весь надходить на ринок, а продається партіями D Q. Мета продавця: утримувати ціну на товар, вищою за рівноважну. Після надходження першої партії товару його кількість на ринку буде Q 1 = D Q. Ціна, що відповідає такій кількості товару, становить Р 1 = f (Q 1). Витрати споживача — Р 1D Q. Після надходження другої партії товару його кількість на ринку буде Q 2 = Q 1 + D Q = 2D Q. Відповідна ціна — Р 2 = f (Q 2). Витрати — Р 2D Q. Після надходження n -ї партії кількість товару — Qn = Q 0 = n D Q. Відповідна ціна — Рn = f (Qn) = Р 1 = f (Q 0) = Р 0. Витрати Рn D Q. Загальні витрати споживачів на всю кількість товару Q 0 становитимуть Р1 D Q + Р2 D Q + … + Рn D Q = f1(Q1) D Q + … f(Qn) D Q. Графічна інтерпретація
Як бачимо з рис. 7, загальні витрати споживачів дорівнюють сумі площ прямокутників, а вона, у свою чергу, наближено дорівнює визначеному інтегралу f(Q1) D Q + f(Q2) D Q + … + f(Qn) D Q Наближена рівність стає точною, якщо n як завгодно велике. Отже, сумарні витрати S вит можна обчислювати за формулою:
Означення. Надлишок споживача S надл — це різниця між можливими витратами споживача і реальними витратами в умовах ринку:
Геометрична інтерпретація
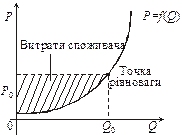
2. Додаткова вартість. Розглянемо криву пропозиції Р = f (Q) (рис. 9).
Рис. 9
Виробники іноді мають можливість поставляти товар на ринок за вищою ціною, ніж та, на яку вони були згодні попередньо. Припускаючи, що весь товар Q 0 буде реалізовано за ціною Р 0, можна знайти дохід R = Р 0 Q 0. Нехай водночас кількість товару, меншу за Q 0, виробники поставляють за ціною, нижчою, ніж Р 0. Тоді додаткова вартість виробника S дод.варт обчислюються за формулою:
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 859; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.66.34 (0.012 с.) |

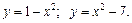 2.
2. 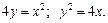 3.
3. 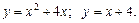 4.
4. 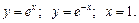
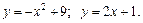 6.
6. 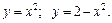 7.
7. 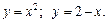
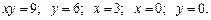
 1. Обчислення площі фігури
1. Обчислення площі фігури 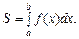 (1)
(1)
 2. Якщо потрібно обчислити площу фігури, обмеженої кривими у = f 1(x), у = f 2(x)(f 1(x) ³ f 2(x)) ординатами х = а і х = b, то
2. Якщо потрібно обчислити площу фігури, обмеженої кривими у = f 1(x), у = f 2(x)(f 1(x) ³ f 2(x)) ординатами х = а і х = b, то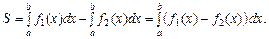 (2)
(2)
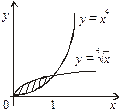
 Обчислити площу фігури, обмеженої кривими
Обчислити площу фігури, обмеженої кривими 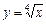 і
і 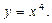
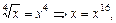
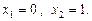
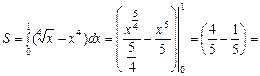
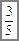 .
.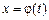 і
і 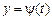 ,
, 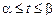 ,
, 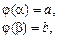 (3)
(3)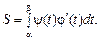 (4)
(4)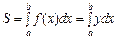
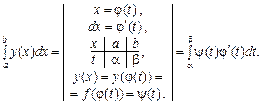
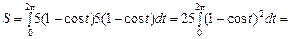
 75p.
75p. 2. Довжина дуги кривої
2. Довжина дуги кривої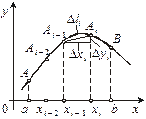
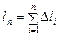 .
.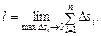 (5)
(5)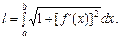 (6)
(6)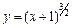 ,
, 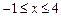 .
.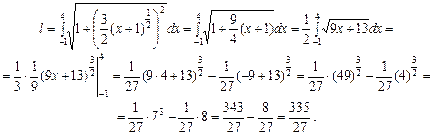
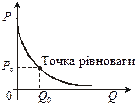
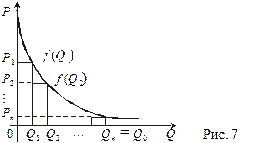
 .
.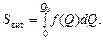 (7)
(7)