
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула для знаходження диференціалаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
справджується в усіх випадках: як тоді, коли u є незалежною змінною, так і тоді, коли u є функцією іншої незалежної змінної. В останньому випадку під множником du слід розуміти диференціал функції u.
·
· До обох частин рівності застосуємо операцію знаходження диференціала:
Звідси
· Диференціали вищих порядків Диференціал функції є також функцією незалежної змінної, а тому його можна диференціювати. Розглянемо функцію Означення. Другим диференціалом функції у = f (x) називається вираз d (dy). Позначення: Аналогічно дістаємо третій диференціал Диференціал незалежної змінної dx не залежить від х, тому, диференціюючи dx за х, слід розглядати dx як величину сталу відносно х. Отже, приходимо до простих співвідношень між послідовними диференціалами і послідовними похідними:
· Згідно з (1) дістаємо:
¨ Справді, при незалежному аргументі х функції f (x) маємо:
Якщо у функції у = f (x) аргумент х є функцією змінної t, тобто х = j(t), то dx вже залежить від t, і dx = j¢(t) dt, тому при x = j(t) дістаємо:
Розглядаючи вирази (1) і (2), доходимо висновку, що форма диференціала другого порядку не зберігається з переходом до складеної функції. Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл.5, стор. 225 – 233
Тема 14 Формула Тейлора Мета заняття:вивести формулу Тейлора представлення функції у вигляді многочлена. Розвивати логічне мислення.
Студенти повинні знати: формулу Тейлора представлення функцій у вигляді многочлена. Студенти повинні вміти: знаходити похідні вищих порядків функцій; користуватися формулою Тейлора представлення функцій у вигляді многочлена; записувати розкладання елементарних функцій за формулою Тейлора.
Основні питання теми 1.Формула Тейлора; 2.Формула Маклорена; 3.Приклади Завдання для самоперевірки 1.За правилом Лопіталя обчислити границі 1. 3. 5. 7. 9. 11. 13. 15. 2.Записати формулу Тейлора для наступних функцій 1. Розкласти многочлен 2. Розкласти многочлен 3. Розкласти многочлен 4. Функцію 5. Записати формулу Тейлора п -го порядку для функції 6. Записати формулу Маклорена п -го порядку для функції 7. Записати формулу Тейлора п -го порядку для функції 8. Записати формулу Маклорена 2 п -го порядку для функції 9. Записати формулу Тейлора п -го порядку для функції 10. Записати формулу Маклорена 2 п -го порядку для функції 11. Записати формулу Тейлора 3-го порядку для функції 12. Записати формулу Тейлора 2-го порядку для функції Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл.5, стор. 238 – 245. Лекція „Формула Тейлора” Нехай функція f (x) має п похідних у точці х 0. Означення. Многочлен
називається многочленом Тейлора функції f(x) у точці х 0. Теорема. Нехай функція f (x) має в e-околі точки х 0 (n + 1) похідну. Тоді для будь-якої точки х із цього околу знайдеться точка с, розміщена між точками х і х 0, для якої справджується рівність:
де Т (х) — п -й многочлен Тейлора функції f (x) у точці х 0. Доведення. Визначимо функцію r (x) формулою
Для цієї функції також виконується рівність
де х 1 — деяка точка, розміщена між точками х 0 і х. Маємо
Крім того, Звідси
де точка х 2 розміщена між х 0 і х 1. Міркуючи так само, застосуємо теорему Коші до співвідношення (3) (п + 1) раз і дістанемо ланцюжок рівностей:
де кожна точка хk +1 розміщена між х 0 і хk (k = 1, …, n). Отже,
де
Узявши с = хn + 1 і врахувавши, що f (x) = T (x) + r (x), дістанемо рівність (1). Формула (1) називається формулою Тейлора, а вираз (4) — залишковим членом у формі Лагранжа. Беручи у формулі (1) х 0 = 0, дістанемо формулу, яку називають формулою Маклорена:
де с — точка, розміщена між 0 і х. Застосування формули Тейлора 1. Рівність
і середнє квадратичне відхилення:
Як визначити середнє арифметичне виду
якщо числа х 1, х 2, …, хn невідомі, але відомий відрізок, якому вони належать? · Значення Замінимо функцію f (x) на многочлен Тейлора другого порядку в точці а:
Тоді
Оскільки
маємо:
· Середнє геометричне можна подати у вигляді:
Використовуючи формулу (7) для функції
Отже, середнє геометричне дорівнює
· Згідно з формулою (8) знаходимо
Далі маємо:
Отже, ціни за 10 років зросли приблизно на 5%. ·
Розклад основних елементарних функцій 1. Розкладемо за формулою Тейлора функцію
Далі за формулою Тейлора (1) маємо:
Зокрема, при х = 1
У цьому розкладі залишковий член прямує до нуля при
Можна записати: Цей вираз називають рядами і позначають так:
2. Розкладемо за формулою Тейлора функцію
.................................................................................. За формулою Тейлора (1) дістанемо (рис. 1)
Рис. 1
● Залишковий член у формулі Тейлора за модулем має бути меншим, ніж 10–8:
Отже, Обчислимо кілька членів розкладу
Остаточно дістанемо:
3. Розклад за формулою Тейлора функції Насамперед обчислимо:
Далі за формулою Тейлора (1) дістанемо:
● Оскільки
Щоб досягти заданої точності, візьмемо
Розклад за формулою Тейлора 1. Розклад функції Насамперед
.................................................................................... За формулою Тейлора отримаємо розклад
Цей розклад названо формулою бінома Ньютона на честь її відкривача. Якщо
● Маємо
● Виконаємо перетворення
2. Розклад функції
За формулою Тейлора (1) дістанемо розклад
або Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл.5, стор. 238 – 245.
Тема 15
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 470; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.214.156 (0.012 с.) |

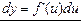
 Зауваження. Оскільки диференціал функції дорівнює добутку її похідної на диференціал незалежної змінної, то формули для знаходження диференціалів будуть такі самі, як і для знаходження похідних, якщо кожну з них помножити на dx.
Зауваження. Оскільки диференціал функції дорівнює добутку її похідної на диференціал незалежної змінної, то формули для знаходження диференціалів будуть такі самі, як і для знаходження похідних, якщо кожну з них помножити на dx. Знайти диференціал функції
Знайти диференціал функції 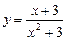 .
.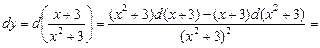
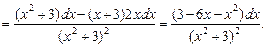 ·
·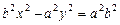 .
.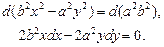
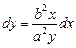 . ·
. ·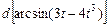 .
.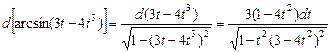 . ·
. · .
.
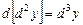 і т. д. до диференціала n -го порядку
і т. д. до диференціала n -го порядку 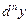 .
. (1)
(1) .
.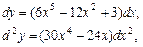
 ·
·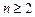 будуть неправильними в загальному випадку, якщо змінна х є функцією від незалежного аргументу t. Виняток становитиме випадок, коли х є лінійною функцією незалежного аргументу t і
будуть неправильними в загальному випадку, якщо змінна х є функцією від незалежного аргументу t. Виняток становитиме випадок, коли х є лінійною функцією незалежного аргументу t і  .
.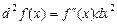 .
. (2)
(2)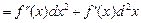 ·
·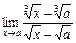 . 2.
. 2.  .
. . 4.
. 4. 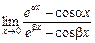 .
.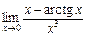 . 6.
. 6. 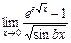 .
.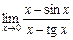 . 8.
. 8.  .
.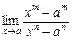 . 10.
. 10. 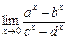 .
. . 12.
. 12.  .
.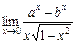 . 14.
. 14. 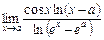 .
.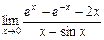 . 16.
. 16. 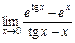 .
.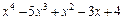 за степенями двочлена
за степенями двочлена 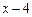 .
. за степенями двочлена
за степенями двочлена 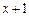 .
.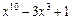 за степенями двочлена
за степенями двочлена  .
.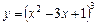 розкласти за степенями х, використовуючи формулу Тейлора.
розкласти за степенями х, використовуючи формулу Тейлора.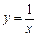 при
при 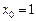 .
.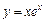 .
.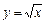 при
при 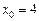 .
.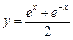 .
.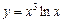 при
при  .
.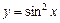 .
.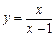 при
при 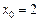 . Побудувати графіки цієї функції і її много-
. Побудувати графіки цієї функції і її много- при
при 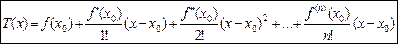
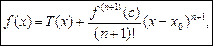 (1)
(1)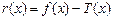 . Оскільки
. Оскільки  , маємо
, маємо 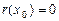 . Визначимо ще одну функцію:
. Визначимо ще одну функцію: .
.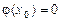 . Тому можна застосувати теорему Коші для перетворення частки функцій r (x) і j(x):
. Тому можна застосувати теорему Коші для перетворення частки функцій r (x) і j(x): , (2)
, (2)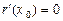 , оскільки
, оскільки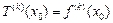 .
.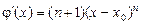 .
.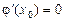 . Застосовуючи теорему Коші до співвідношення (2), дістаємо:
. Застосовуючи теорему Коші до співвідношення (2), дістаємо: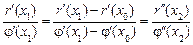 , (3)
, (3)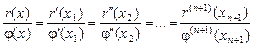 ,
,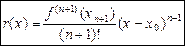 , (4)
, (4) ,
,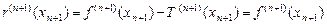 .
.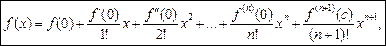
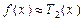 застосовується в задачах економічної статистики. Наприклад, розглянемо таку задачу.
застосовується в задачах економічної статистики. Наприклад, розглянемо таку задачу. Припустимо, що для чисел відомо середнє арифметичне
Припустимо, що для чисел відомо середнє арифметичне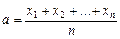
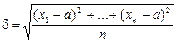 .
.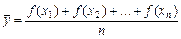 ,
,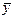 можна, очевидно, знайти лише наближено. При цьому похідна буде настільки малою, наскільки малим буде максимальне значення
можна, очевидно, знайти лише наближено. При цьому похідна буде настільки малою, наскільки малим буде максимальне значення 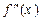 на відрізку, який містить х 1, х 2, …, хn.
на відрізку, який містить х 1, х 2, …, хn. .
.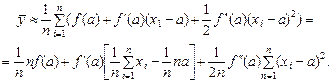
 ,
,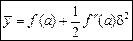 . · (7)
. · (7)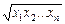 .
.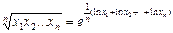 .
.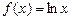 , одержимо
, одержимо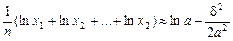 .
.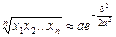 . (8)
. (8) — індекс споживчих цін за цей рік. Відомо, що середнє арифметичне чисел k 1, k 2, …, kn дорівнює 1, а середнє квадратичне відхилення δ = 1. Визначити відносну зміну споживчих цін з 1 січня і -го року по 1 січня (і +10)го року.
— індекс споживчих цін за цей рік. Відомо, що середнє арифметичне чисел k 1, k 2, …, kn дорівнює 1, а середнє квадратичне відхилення δ = 1. Визначити відносну зміну споживчих цін з 1 січня і -го року по 1 січня (і +10)го року.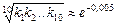 .
. .
.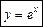 у
у 
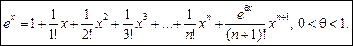 (9)
(9)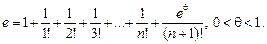
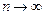 :
: .
.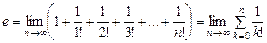 .
.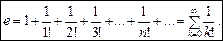 (10)
(10)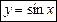 у
у 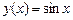 ,
, 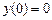 ;
;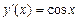 ,
, 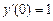 ;
; ,
,  ;
;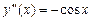 ,
,  ;
;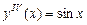
 ;
;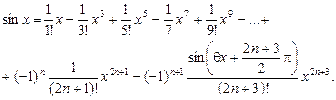 (11)
(11)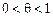 .
.
 з точністю до 10–8 при
з точністю до 10–8 при 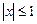 .
.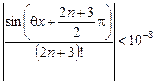 .
.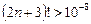 .
. при
при ;
;
 ;
;
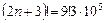 ;
;
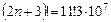 ;
;
 .
.

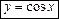 в т. х 0 = 0.
в т. х 0 = 0.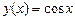 ,
,  ;
;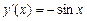 ,
,  ;
; ,
, 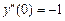 ;
;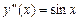 ,
, 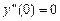 ;
; ,
, 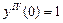 .
. (12)
(12)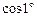 з точністю до 10–10.
з точністю до 10–10.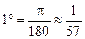 , то
, то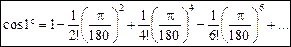
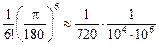 .
.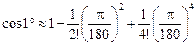 ●
●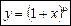 ,
, 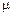 — довільне число.
— довільне число. ,
,
 ,
,
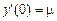 ;
;
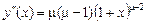 ,
,
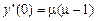 ;
;
 ,
,
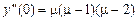 .
.
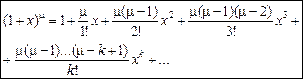 (13)
(13)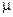 — натуральне число, то розклад містить скінченне число доданків.
— натуральне число, то розклад містить скінченне число доданків.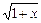 .
.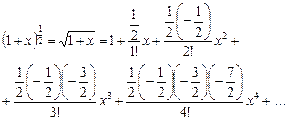 ;
;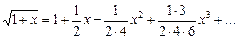 .
.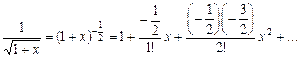
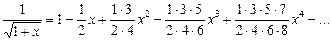 .
.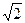 .
.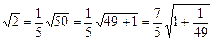 ;
;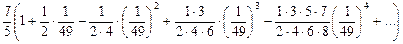 .
.
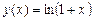 ,
,
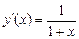 ,
,
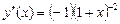 ,
,
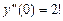 ;
;
 ,
,
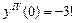 ;
;
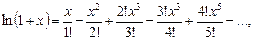
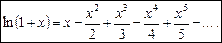 (14)
(14)


