
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Шуканий об’єм Знаходимо за формулоюСодержание книги
Поиск на нашем сайте
Для обчислення другого інтегралу використовуємо підстановку
3. Знайти площу фігури, обмеженої кривими заданими в полярних координатах:
Розв’язування. Задана фігура обмежена двома променями Її площа дорівнює
Завдання 5-6. Нехай При обчисленні частинної похідної
Аналогічно обчислюємо
Завдання 7. Нехай задано функцію Для цього обчислимо частинні похідні функції Обчислюємо значення цих похідних в точці
Градієнт grad u функції u(x, y) обчислюється за формулою
Таким чином,
Похідна в напрямку вектора
де
Отримуємо:
Завдання 8. Знайти загальний розв’язок (загальний інтеграл) диференціального рівняння
Розв’язування. Права частина рівняння
Продовжуємо перетворення:
Відокремлюємо змінні:
Після інтегрування обох частин рівняння отримуємо
Таким чином,
Потенціюючи, знаходимо
або
Остаточно, загальний інтеграл вихідного рівняння набуває вигляду:
де С – довільна стала.
Завдання 9. Розв’язати рівняння Розв’язування. Маємо рівняння виду
Це рівняння розпадається на два:
З першого маємо
Оскільки Замінивши Отже, задане рівняння має розв’язки
Завдання 10. Знайти загальний розв’язок неоднорідного диференціального рівняння другого порядку із сталими коефіцієнтами
Розв’язування. Знайдемо загальний розв’язок
Для цього складаємо характеристичне рівняння і знаходимо його корені.
Так як корені характеристичного рівняння є дійсними і різними, то загальний розв’язок однорідного рівняння записується у вигляді
де Підбираємо тепер частинний розв’язок заданого неоднорідного рівняння у вигляді (врахуємо що
Звідси
або після спрощення
Звідси отримуємо рівності
Таким чином, загальний розв’язок заданого неоднорідного диференціального рівняння має вигляд
Знайдемо частинний розв’язок, який задовольняє задані початкові умови. Продиференціюємо загальний розв’язок:
Підставивши в загальний розв’язок і його похідну початкові умови
Звідки
Завдання 11. Нехай задано систему лінійних диференціальних рівнянь першого порядку Продиференціюємо перше рівняння
Запитання для самоконтролю 1. Сформулюйте означення первісної функції і невизначеного інтеграла. 2. Випишіть таблицю основних інтегралів. 3. Сформулюйте основні методи інтегрування. 4. Виведіть формули інтегрування елементарних дробів. 5. Сформулюйте правило розкладу правильного дробу на суму елементарних. 6. Виведіть універсальну тригонометричну підстановку. 7. Наведіть методи інтегрування деяких тригонометричних функцій, проілюструйте їх прикладами. 8. Наведіть методи інтегрування деяких ірраціональних функцій, проілюструйте їх прикладами. 9. В чому полягає задача про площу криволінійної трапеції, роботу сили, шлях? 10. Що називається визначеним інтегралом? 11. Сформулювати і довести основні властивості визначеного інтеграла. 12. Довести формулу Ньютона-Лейбніца. 13. В чому полягає метод заміни змінної у визначеному інтегралі? 14. Що називається невласним інтегралом першого роду? невласним інтегралом другого роду? 15. Як обчислити площу плоскої фігури в декартових та полярних координатах? 16. Що називається функцією двох змінних? 17. Дати означення частинної похідної функції двох змінних по одній з них. 18. Що називається скалярним полем? Навести приклади. 19. Дати означення похідної за напрямом, записати формулу для обчислення похідної за напрямом. 20. Дати означення градієнта скалярного поля. Сформулювати властивості градієнта. 21. Що називається диференціальним рівнянням першого порядку? 22. Сформулювати теорему Коші про існування та єдиність розв’язку рівняння першого порядку. 23. Вказати типи диференціальних рівнянь першого порядку, що інтегруються в квадратурах, методи їх розв’язання. 24. У чому суть методу пониження порядку диференціального рівняння? 25. Як звести до рівнянь першого порядку рівняння 26. Структура загального розв’язку лінійного неоднорідного рівняння другого порядку. 27. Як знаходиться частинний розв’язок неоднорідного диференціального рівняння другого порядку? 28. Викласти схему розв’язання системи диференціальних рівнянь методом виключення.
|
||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 405; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |


 Тоді
Тоді  і
і 
 Звідси
Звідси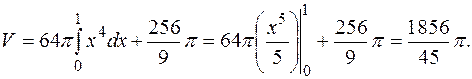
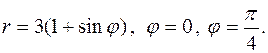

 і кривою
і кривою 



 змінну у розглядаємо як сталу величину. Користуючись правилами диференціювання функцій одного аргументу і правилом диференціювання складеної функції, отримуємо
змінну у розглядаємо як сталу величину. Користуючись правилами диференціювання функцій одного аргументу і правилом диференціювання складеної функції, отримуємо
 . Вважаючи х сталою величиною, отримуємо
. Вважаючи х сталою величиною, отримуємо
 . Знайдемо градієнт і похідну цієї функції в точці
. Знайдемо градієнт і похідну цієї функції в точці  в напрямку вектора
в напрямку вектора  .
.




 обчислюється за формулою
обчислюється за формулою

 ,
,  ;
;  .
.
 .
. має властивість
має властивість  Тому задане рівняння є однорідним диференціальним рівнянням першого порядку. Виконаємо заміну
Тому задане рівняння є однорідним диференціальним рівнянням першого порядку. Виконаємо заміну  , де
, де  – деяка функція від аргументу х. Звідси
– деяка функція від аргументу х. Звідси  . Вихідне рівняння приймає вигляд:
. Вихідне рівняння приймає вигляд: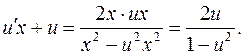










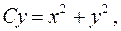
 .
. . Поклавши
. Поклавши , дістанемо
, дістанемо  або
або  .
. .
. , звідки
, звідки  . У другому рівнянні відокремлюються змінні:
. У другому рівнянні відокремлюються змінні: .
. , то
, то  .
. на
на  ,
,  на
на  , знайдемо другий розв’язок даного рівняння:
, знайдемо другий розв’язок даного рівняння:  .
. ,
,  ,
, 
 однорідного рівняння з тими ж коефіцієнтами, що і в лівій частині заданого рівняння:
однорідного рівняння з тими ж коефіцієнтами, що і в лівій частині заданого рівняння:
 ,
, .
.
 – довільні сталі.
– довільні сталі. є корінь характеристичного рівняння)
є корінь характеристичного рівняння)

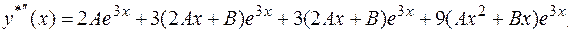 Підставляємо
Підставляємо  у вихідне рівняння і скоротивши всі доданки на множник
у вихідне рівняння і скоротивши всі доданки на множник  , отримуємо
, отримуємо


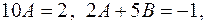 тобто
тобто

 .
.
 ,
,  , дістаємо систему рівнянь
, дістаємо систему рівнянь ,
, . Отже,
. Отже, - шуканий розв’язок.
- шуканий розв’язок. .
. Із другого рівняння підставимо
Із другого рівняння підставимо  , отримаємо
, отримаємо  значення у візьмемо із першого рівняння, тобто
значення у візьмемо із першого рівняння, тобто  , тоді
, тоді  або
або  тобто отримали лінійне однорідне диференціальне рівняння другого порядку. Записуємо і розв’язуємо його характеристичне рівняння
тобто отримали лінійне однорідне диференціальне рівняння другого порядку. Записуємо і розв’язуємо його характеристичне рівняння  ,
,  ,
,  . Тобто загальний розв’язок має вигляд:
. Тобто загальний розв’язок має вигляд:  . Оскільки
. Оскільки  . Тоді
. Тоді  . Отже, розв’язок системи має вигляд
. Отже, розв’язок системи має вигляд  .
. та
та 



