
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтегрування тригонометричних функцій.Содержание книги
Поиск на нашем сайте
Інтеграли виду а) якщо б) якщо в) якщо Інтегрування деяких ірраціональних функцій. 1. Інтеграл виду 2. Інтеграли виду а) а) зводяться до інтегралів від тригонометричних функцій. 3. Інтеграл виду
Визначений інтеграл Нехай функція Означення. Якщо існує границя інтегральної суми
Число Якщо Основні методи обчислення визначеного інтеграла – інтегрування частинами і заміна змінної. Якщо
Заміна змінної у визначеному інтегралі:
Важливо те, що заміняючи змінну у визначеному інтегралі, знаходять також нові межі інтегрування, і надалі вже не повертаються до початкової змінної. Якщо функція
Якщо неперервна на
Площа фігури, обмеженої кривими
Площа криволінійного сектора, обмеженого кривою
Якщо крива задана параметричними рівняннями
Довжина дуги Об’єм тіла, утвореного обертанням криволінійної трапеції, обмеженої лініями
За допомогою визначеного інтеграла обчислюють також статичні моменти і моменти інерції плоских фігур, знаходять координати центра мас плоскої фігури, роботу, тиск та інші величини. Функції багатьох змінних. Нехай задано множину Множину Впорядкованій парі чисел Нехай функція Величини
називають частинними приростами функції Якщо існує границя
то вона називається частинною похідною функції Аналогічно частинна похідна функції
і позначається одним із символів: Частинними похідними другого порядку від функції
Похідні Нехай задано скалярне поле, тобто скалярна функція Якщо існує границя
то її називають похідною функції Похідну за напрямом обчислюють за формулою:
Градієнтом функції
Градієнт вказує напрям максимального зростання скалярного поля.
|
||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.33.17 (0.007 с.) |

 універсальною підстановкою
універсальною підстановкою  ,
,  ,
,  ,
,  зводяться до інтегралів від раціональних дробів. Проте, в деяких випадках зручніше скористатись іншими підстановками, наприклад:
зводяться до інтегралів від раціональних дробів. Проте, в деяких випадках зручніше скористатись іншими підстановками, наприклад: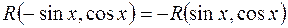 , то
, то  ;
; , то
, то  ;
; , то
, то  .
. ,
,  раціоналізується підстановкою
раціоналізується підстановкою  .
. , б)
, б)  , в)
, в) 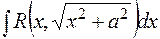 підстановками
підстановками , б)
, б)  , в)
, в) 
 підстановкою
підстановкою  зводиться до одного з інтегралів попереднього типу.
зводиться до одного з інтегралів попереднього типу. визначена на відрізку
визначена на відрізку  і
і  – довільне розбиття цього відрізка на
– довільне розбиття цього відрізка на  частинних відрізків
частинних відрізків  ,
,  . На кожному з них виберемо довільну точку
. На кожному з них виберемо довільну точку  і складемо суму
і складемо суму  ,
,  . Число
. Число  називається інтегральною сумою функції
називається інтегральною сумою функції  ,
,  .
. , що не залежить ні від способу розбиття відрізка
, що не залежить ні від способу розбиття відрізка  , тобто
, тобто .
. називають нижньою, число
називають нижньою, число  – верхньою межею визначеного інтеграла.
– верхньою межею визначеного інтеграла. - первісна для
- первісна для  на
на  (формула Ньютона-Лейбніца). Різницю
(формула Ньютона-Лейбніца). Різницю  записують також у вигляді
записують також у вигляді  .
. і
і  - неперервно диференційовні функції на
- неперервно диференційовні функції на 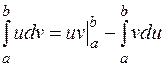 .
. , де
, де  - функція, неперервна разом зі своєю похідною
- функція, неперервна разом зі своєю похідною  на відрізку
на відрізку  ;
;  ,
,  ,
,  - функція неперервна на
- функція неперервна на  .
. , то невласний інтеграл з нескінченною верхньою межею знаходять як границю визначеного інтеграла:
, то невласний інтеграл з нескінченною верхньою межею знаходять як границю визначеного інтеграла:  . Відповідно
. Відповідно .
. функція
функція  необмежено зростає і в точці
необмежено зростає і в точці  невизначена, то за означенням
невизначена, то за означенням , де e >0.
, де e >0. і
і 
 та прямими
та прямими  і
і  знаходиться за формулою
знаходиться за формулою .
. і полярними радіусами
і полярними радіусами  та
та  , виражається інтегралом
, виражається інтегралом .
. ,
, 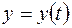 ,
,  , то площа відповідної криволінійної трапеції
, то площа відповідної криволінійної трапеції .
. гладкої кривої
гладкої кривої  ,
,  знаходиться за формулою
знаходиться за формулою  . Якщо крива задана параметричними рівняннями
. Якщо крива задана параметричними рівняннями  , то
, то 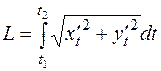 . Довжина дуги
. Довжина дуги  .
. , навколо осі
, навколо осі 
 .
. впорядкованих пар чисел
впорядкованих пар чисел  . Якщо кожній парі чисел
. Якщо кожній парі чисел 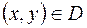 за певним законом відповідає число
за певним законом відповідає число  , то кажуть, що на множині
, то кажуть, що на множині  і
і  і записують
і записують  .
. відповідає єдина точка
відповідає єдина точка  площини, тому функцію
площини, тому функцію  , де
, де  , можна розглядати як функцію точки
, можна розглядати як функцію точки  і замість
і замість  .
. , а змінній
, а змінній  так, щоб точки
так, щоб точки  і
і  належали даному околу.
належали даному околу. ,
,
 відповідно по змінних
відповідно по змінних  ,
, ,
,  ,
,  ,
,  .
.
 ,
,  ,
,  ,
,  .
. ;
; 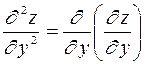 ;
; ;
;  .
.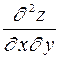 та
та  називають мішаними частинними похідними другого порядку.
називають мішаними частинними похідними другого порядку. разом з областю її визначення. Візьмемо в ньому точку
разом з областю її визначення. Візьмемо в ньому точку  і проведемо з цієї точки вектор
і проведемо з цієї точки вектор  , напрямні косинуси якого
, напрямні косинуси якого  ,
,  ,
, 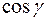 . На векторі
. На векторі  від його початку візьмемо точку
від його початку візьмемо точку  . Обчислимо приріст
. Обчислимо приріст  функції
функції 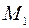 в напрямі вектора
в напрямі вектора  .
. ,
, .
. .
. . Отже,
. Отже, .
.


