
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтегрування раціональних дробів.Содержание книги
Поиск на нашем сайте
Теоретичні відомості Інтегральне числення. Невизначений інтеграл
Функція Якщо Множина всіх первісних для функції
Таблиця основних інтегралів: 1. 3. 5. 7. 9. 11. 13. 15. 17. 18. Основні методи інтегрування – інтегрування частинами і заміна змінної. Існують два способи заміни змінної: введення під знак диференціала і підстановка. Метод введення під знак диференціала виражається формулою
де Метод підстановки полягає в тому, що коли функція Метод інтегрування частинами виражається формулою
де Далеко не кожну функцію можна проінтегрувати одним з вищеназваних способів. Наприклад: Наведемо основні типи інтегрованих функцій. Інтегрування раціональних дробів. Якщо степінь многочлена, який стоїть у чисельнику, більший або дорівнює степені многочлена, який стоїть у знаменнику, то такий раціональний дріб називається неправильним. Виділенням цілої частини неправильного дробу задача інтегрування зводиться до знаходження первісної правильного дробу. Далі правильний дріб потрібно розкласти на суму елементарних дробів виду
де
Інтегрування тригонометричних функцій. Інтеграли виду а) якщо б) якщо в) якщо Інтегрування деяких ірраціональних функцій. 1. Інтеграл виду 2. Інтеграли виду а) а) зводяться до інтегралів від тригонометричних функцій. 3. Інтеграл виду
Визначений інтеграл Нехай функція
Означення. Якщо існує границя інтегральної суми
Число Якщо Основні методи обчислення визначеного інтеграла – інтегрування частинами і заміна змінної. Якщо
Заміна змінної у визначеному інтегралі:
Важливо те, що заміняючи змінну у визначеному інтегралі, знаходять також нові межі інтегрування, і надалі вже не повертаються до початкової змінної. Якщо функція
Якщо неперервна на
Площа фігури, обмеженої кривими
Площа криволінійного сектора, обмеженого кривою
Якщо крива задана параметричними рівняннями
Довжина дуги Об’єм тіла, утвореного обертанням криволінійної трапеції, обмеженої лініями
За допомогою визначеного інтеграла обчислюють також статичні моменти і моменти інерції плоских фігур, знаходять координати центра мас плоскої фігури, роботу, тиск та інші величини. Функції багатьох змінних. Нехай задано множину
Множину Впорядкованій парі чисел Нехай функція Величини
називають частинними приростами функції Якщо існує границя
то вона називається частинною похідною функції Аналогічно частинна похідна функції
і позначається одним із символів: Частинними похідними другого порядку від функції
Похідні Нехай задано скалярне поле, тобто скалярна функція Якщо існує границя
то її називають похідною функції Похідну за напрямом обчислюють за формулою:
Градієнтом функції
Градієнт вказує напрям максимального зростання скалярного поля. Контрольна робота №1 Завдання 1. 1. Знайти інтеграл
Перевіримо диференціюванням вірність отриманого розв’язку. Для цього знайдемо похідну
Отримали підінтегральну функцію. 2. Знайти інтеграл
3. Знайти інтеграл Використаємо формулу інтегрування частинами
Нехай
Перевіримо диференціюванням вірність отриманого розв’язку. Для цього знайдемо похідну
= Отримали підінтегральну функцію. 4. Знайти інтеграл Перетворимо знаменник дробу, що стоїть під знаком інтеграла наступним чином:
Тоді після підстановки
При обчисленні інтеграла
5. Обчислити інтеграл Підінтегральна функція – неправильний дріб, тому, розділивши чисельник на знаменник, виділимо цілу частину
Правильний дріб розкладемо на суму елементарних дробів
де А, В, С, D – невизначені коефіцієнти. Звідси
Надамо х чотири різних значення (по кількості невизначених коефіцієнтів):
Розв’язавши систему лінійних рівнянь отримаємо Тоді
Остаточно маємо
6. Обчислити інтеграл Виконаємо підстановку
7. Знайти інтеграл Скористаємося універсальною тригонометричною підстановкою
Завдання 2. 1. Нехай необхідно обчислити інтеграл Використаємо формулу Ньютона–Лейбніца
Щоб обчислити визначений інтеграл
2. Обчислити інтеграл При обчисленні даного інтегралу зробимо заміну змінної. В цьому випадку знаходимо нові границі інтегрування для нової змінної.
Завдання 3. Обчислити інтеграл.
Завдання 4. 1. Обчислити площу фігури, обмеженої заданими параболами
Розв’язування. Знайдемо абсциси точок перетину заданих парабол. Для цього прирівняємо праві частини цих рівнянь:
Звідси
де В нашому випадку маємо
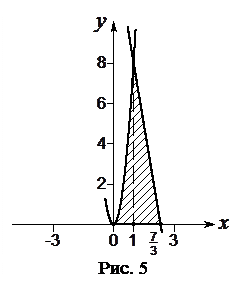
2. Знайти об’єм тіла, утвореного обертанням навколо осі Ох фігури, розташованої в першій координатній чверті і обмеженої параболою Розв’язування. Знайдемо абсцису точки перетину параболи і прямої в першій координатній чверті. Для цього розв’яжемо рівняння
Абсцису точки перетину прямої з віссю Ох знайдемо, розв’язавши рівняння Таким чином, можемо вважати, що тіло обертання обмежене при Завдання 5-6. Нехай При обчисленні частинної похідної
Аналогічно обчислюємо
Завдання 7. Нехай задано функцію Для цього обчислимо частинні похідні функції Обчислюємо значення цих похідних в точці
Градієнт grad u функції u(x, y) обчислюється за формулою
Таким чином,
Похідна в напрямку вектора
де
Отримуємо:
Завдання 8. Знайти загальний розв’язок (загальний інтеграл) диференціального рівняння
Розв’язування. Права частина рівняння
Продовжуємо перетворення:
Відокремлюємо змінні:
Після інтегрування обох частин рівняння отримуємо
Таким чином,
Потенціюючи, знаходимо
або
Остаточно, загальний інтеграл вихідного рівняння набуває вигляду:
де С – довільна стала.
Завдання 9. Розв’язати рівняння Розв’язування. Маємо рівняння виду
Це рівняння розпадається на два:
З першого маємо
Оскільки Замінивши Отже, задане рівняння має розв’язки
Завдання 10. Знайти загальний розв’язок неоднорідного диференціального рівняння другого порядку із сталими коефіцієнтами
Розв’язування. Знайдемо загальний розв’язок
Для цього складаємо характеристичне рівняння і знаходимо його корені.
Так як корені характеристичного рівняння є дійсними і різними, то загальний розв’язок однорідного рівняння записується у вигляді
де Підбираємо тепер частинний розв’язок заданого неоднорідного рівняння у вигляді (врахуємо що
Звідси
або після спрощення
Звідси отримуємо рівності
Таким чином, загальний розв’язок заданого неоднорідного диференціального рівняння має вигляд
Знайдемо частинний розв’язок, який задовольняє задані початкові умови. Продиференціюємо загальний розв’язок:
Підставивши в загальний розв’язок і його похідну початкові умови
Звідки
Завдання 11. Нехай задано систему лінійних диференціальних рівнянь першого порядку Продиференціюємо перше рівняння
Запитання для самоконтролю 1. Сформулюйте означення первісної функції і невизначеного інтеграла. 2. Випишіть таблицю основних інтегралів. 3. Сформулюйте основні методи інтегрування. 4. Виведіть формули інтегрування елементарних дробів. 5. Сформулюйте правило розкладу правильного дробу на суму елементарних. 6. Виведіть універсальну тригонометричну підстановку. 7. Наведіть методи інтегрування деяких тригонометричних функцій, проілюструйте їх прикладами. 8. Наведіть методи інтегрування деяких ірраціональних функцій, проілюструйте їх прикладами. 9. В чому полягає задача про площу криволінійної трапеції, роботу сили, шлях? 10. Що називається визначеним інтегралом? 11. Сформулювати і довести основні властивості визначеного інтеграла. 12. Довести формулу Ньютона-Лейбніца. 13. В чому полягає метод заміни змінної у визначеному інтегралі? 14. Що називається невласним інтегралом першого роду? невласним інтегралом другого роду? 15. Як обчислити площу плоскої фігури в декартових та полярних координатах? 16. Що називається функцією двох змінних? 17. Дати означення частинної похідної функції двох змінних по одній з них. 18. Що називається скалярним полем? Навести приклади. 19. Дати означення похідної за напрямом, записати формулу для обчислення похідної за напрямом.
20. Дати означення градієнта скалярного поля. Сформулювати властивості градієнта. 21. Що називається диференціальним рівнянням першого порядку? 22. Сформулювати теорему Коші про існування та єдиність розв’язку рівняння першого порядку. 23. Вказати типи диференціальних рівнянь першого порядку, що інтегруються в квадратурах, методи їх розв’язання. 24. У чому суть методу пониження порядку диференціального рівняння? 25. Як звести до рівнянь першого порядку рівняння 26. Структура загального розв’язку лінійного неоднорідного рівняння другого поряд
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-26; просмотров: 654; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.166.126 (0.013 с.) |

 називається первісною для функції
називається первісною для функції  на проміжку
на проміжку  , якщо
, якщо  ,
,  .
. також буде первісною для
також буде первісною для  .
.
 2.
2. 
 4.
4. 
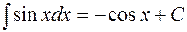 6.
6. 
 8.
8. 
 10.
10. 
 12.
12. 
 14.
14. 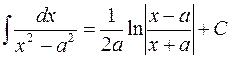
 16.
16. 


 ,
, - первісна для
- первісна для  ,
,  - неперервна диференційовна функція.
- неперервна диференційовна функція. , де
, де 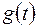 ,
,  - неперервні, отримуємо
- неперервні, отримуємо  .
. ,
, і
і  - диференційовні функції.
- диференційовні функції. ,
,  ,
,  - інтеграли, які “не беруться”.
- інтеграли, які “не беруться”. ,
,  ,
,  ,
,  ,
, ; A, B, a, p, q - константи;
; A, B, a, p, q - константи;  .
. універсальною підстановкою
універсальною підстановкою  ,
,  ,
,  ,
,  зводяться до інтегралів від раціональних дробів. Проте, в деяких випадках зручніше скористатись іншими підстановками, наприклад:
зводяться до інтегралів від раціональних дробів. Проте, в деяких випадках зручніше скористатись іншими підстановками, наприклад: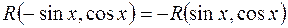 , то
, то  ;
; , то
, то  ;
; , то
, то  .
. ,
,  раціоналізується підстановкою
раціоналізується підстановкою  .
. , б)
, б)  , в)
, в) 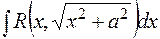 підстановками
підстановками , б)
, б)  , в)
, в) 
 підстановкою
підстановкою  зводиться до одного з інтегралів попереднього типу.
зводиться до одного з інтегралів попереднього типу. і
і  – довільне розбиття цього відрізка на
– довільне розбиття цього відрізка на  частинних відрізків
частинних відрізків  ,
,  . На кожному з них виберемо довільну точку
. На кожному з них виберемо довільну точку  і складемо суму
і складемо суму  ,
,  . Число
. Число  називається інтегральною сумою функції
називається інтегральною сумою функції  ,
,  .
. , що не залежить ні від способу розбиття відрізка
, що не залежить ні від способу розбиття відрізка  , тобто
, тобто .
. називають нижньою, число
називають нижньою, число  – верхньою межею визначеного інтеграла.
– верхньою межею визначеного інтеграла. (формула Ньютона-Лейбніца). Різницю
(формула Ньютона-Лейбніца). Різницю  записують також у вигляді
записують також у вигляді  .
. і
і  - неперервно диференційовні функції на
- неперервно диференційовні функції на 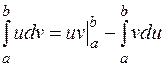 .
. , де
, де  - функція, неперервна разом зі своєю похідною
- функція, неперервна разом зі своєю похідною  на відрізку
на відрізку  ;
;  ,
,  ,
,  - функція неперервна на
- функція неперервна на  .
. , то невласний інтеграл з нескінченною верхньою межею знаходять як границю визначеного інтеграла:
, то невласний інтеграл з нескінченною верхньою межею знаходять як границю визначеного інтеграла:  . Відповідно
. Відповідно .
. функція
функція  необмежено зростає і в точці
необмежено зростає і в точці  невизначена, то за означенням
невизначена, то за означенням , де e >0.
, де e >0. і
і 
 та прямими
та прямими  і
і  знаходиться за формулою
знаходиться за формулою .
. і полярними радіусами
і полярними радіусами  та
та  , виражається інтегралом
, виражається інтегралом .
. ,
, 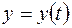 ,
,  , то площа відповідної криволінійної трапеції
, то площа відповідної криволінійної трапеції .
. гладкої кривої
гладкої кривої  ,
,  знаходиться за формулою
знаходиться за формулою  . Якщо крива задана параметричними рівняннями
. Якщо крива задана параметричними рівняннями  , то
, то 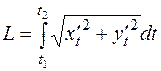 . Довжина дуги
. Довжина дуги  .
. , навколо осі
, навколо осі 
 .
. впорядкованих пар чисел
впорядкованих пар чисел  . Якщо кожній парі чисел
. Якщо кожній парі чисел 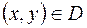 за певним законом відповідає число
за певним законом відповідає число  , то кажуть, що на множині
, то кажуть, що на множині  і
і  і записують
і записують  .
. відповідає єдина точка
відповідає єдина точка  площини, тому функцію
площини, тому функцію  , де
, де  , можна розглядати як функцію точки
, можна розглядати як функцію точки  і замість
і замість  .
. , а змінній
, а змінній  так, щоб точки
так, щоб точки  і
і  належали даному околу.
належали даному околу. ,
,
 відповідно по змінних
відповідно по змінних  ,
, ,
,  ,
,  ,
,  .
.
 ,
,  ,
,  ,
,  .
. ;
; 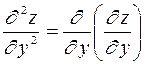 ;
; ;
;  .
.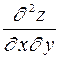 та
та  називають мішаними частинними похідними другого порядку.
називають мішаними частинними похідними другого порядку. разом з областю її визначення. Візьмемо в ньому точку
разом з областю її визначення. Візьмемо в ньому точку  і проведемо з цієї точки вектор
і проведемо з цієї точки вектор  , напрямні косинуси якого
, напрямні косинуси якого  ,
,  ,
, 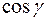 . На векторі
. На векторі  від його початку візьмемо точку
від його початку візьмемо точку  . Обчислимо приріст
. Обчислимо приріст  функції
функції 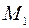 в напрямі вектора
в напрямі вектора  .
. ,
, .
. .
. . Отже,
. Отже, .
. .
.

 .
. .
. .
. (1)
(1) ,
,  . Тоді
. Тоді  ,
,  . Далі за формулою (1) маємо
. Далі за формулою (1) маємо .
.


 .
.
 , dt=dx отримуємо
, dt=dx отримуємо

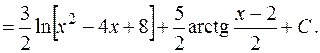
 користувались заміною змінної
користувались заміною змінної  . Тоді
. Тоді  , звідки
, звідки
 .
. .
. ,
, .
. , тоді
, тоді 
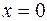 , тоді
, тоді 
 , тоді
, тоді 
 , тоді
, тоді  .
. ,
, ,
,  ,
,  ,
,  .
.
 В знаменнику останнього інтегралу виділимо повний квадрат
В знаменнику останнього інтегралу виділимо повний квадрат  і введемо заміну
і введемо заміну  ,
,  ,
,  :
:
 .
. .
.
 тоді
тоді 
 Отримуємо
Отримуємо
 .
. ,
,
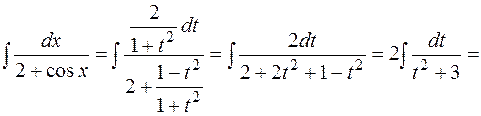
 .
. .
.
 потрібно знайти первісну функцію
потрібно знайти первісну функцію  і замість змінної х спочатку підставити верхню межу b, а потім нижню межу a і від першого результату відняти другий.
і замість змінної х спочатку підставити верхню межу b, а потім нижню межу a і від першого результату відняти другий.
 .
.

 .
. .
.
 .
.



 Площу фігури обчислюємо за формулою
Площу фігури обчислюємо за формулою
 – криві, які обмежують фігуру
– криві, які обмежують фігуру  .
.

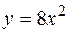 , прямою
, прямою  і віссю Ох.
і віссю Ох.
 або
або 
 Знаходимо, що
Знаходимо, що  Першій координатній чверті відповідає корінь
Першій координатній чверті відповідає корінь 
 звідки
звідки 
 поверхнею, яка утворена обертанням параболи
поверхнею, яка утворена обертанням параболи  – обертанням прямої
– обертанням прямої 
 змінну у розглядаємо як сталу величину. Користуючись правилами диференціювання функцій одного аргументу і правилом диференціювання складеної функції, отримуємо
змінну у розглядаємо як сталу величину. Користуючись правилами диференціювання функцій одного аргументу і правилом диференціювання складеної функції, отримуємо
 . Вважаючи х сталою величиною, отримуємо
. Вважаючи х сталою величиною, отримуємо
 . Знайдемо градієнт і похідну цієї функції в точці
. Знайдемо градієнт і похідну цієї функції в точці  в напрямку вектора
в напрямку вектора  .
.




 обчислюється за формулою
обчислюється за формулою

 ,
,  ;
;  .
.
 .
. має властивість
має властивість  Тому задане рівняння є однорідним диференціальним рівнянням першого порядку. Виконаємо заміну
Тому задане рівняння є однорідним диференціальним рівнянням першого порядку. Виконаємо заміну  , де
, де  – деяка функція від аргументу х. Звідси
– деяка функція від аргументу х. Звідси  . Вихідне рівняння приймає вигляд:
. Вихідне рівняння приймає вигляд: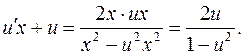










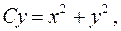
 .
. . Поклавши
. Поклавши , дістанемо
, дістанемо  або
або  .
. .
. , звідки
, звідки  . У другому рівнянні відокремлюються змінні:
. У другому рівнянні відокремлюються змінні: .
. , то
, то  .
. на
на  ,
,  на
на  , знайдемо другий розв’язок даного рівняння:
, знайдемо другий розв’язок даного рівняння:  .
. ,
,  ,
, 
 однорідного рівняння з тими ж коефіцієнтами, що і в лівій частині заданого рівняння:
однорідного рівняння з тими ж коефіцієнтами, що і в лівій частині заданого рівняння:
 ,
, .
.
 – довільні сталі.
– довільні сталі. є корінь характеристичного рівняння)
є корінь характеристичного рівняння)

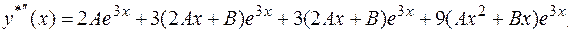 Підставляємо
Підставляємо  у вихідне рівняння і скоротивши всі доданки на множник
у вихідне рівняння і скоротивши всі доданки на множник  , отримуємо
, отримуємо


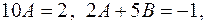 тобто
тобто

 .
.
 , дістаємо систему рівнянь
, дістаємо систему рівнянь ,
, . Отже,
. Отже, - шуканий розв’язок.
- шуканий розв’язок. .
. Із другого рівняння підставимо
Із другого рівняння підставимо  , отримаємо
, отримаємо  значення у візьмемо із першого рівняння, тобто
значення у візьмемо із першого рівняння, тобто  , тоді
, тоді  або
або  тобто отримали лінійне однорідне диференціальне рівняння другого порядку. Записуємо і розв’язуємо його характеристичне рівняння
тобто отримали лінійне однорідне диференціальне рівняння другого порядку. Записуємо і розв’язуємо його характеристичне рівняння  ,
,  ,
,  . Тобто загальний розв’язок має вигляд:
. Тобто загальний розв’язок має вигляд:  . Оскільки
. Оскільки  . Тоді
. Тоді  . Отже, розв’язок системи має вигляд
. Отже, розв’язок системи має вигляд  .
. та
та 



