
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основи диференціального численняСодержание книги
Поиск на нашем сайте
1. Похідною функції називають: A) границю відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля ; 2. Похідна функції Е)
3. Похідна функції y = sin 3 x рівна: В) 3 cos 3 x; 4. Мінімум функція B) – на +; 5. Диференціювання функції В)
6. Функція є монотонно спадною, якщо: А) перша похідна < 0; . 7. Похідна від складеної функції С) 8. Найбільше значення функції В) 19;
9. Частинна похідна функції двох змінних z = x 2 + 2 y 2 по змінній у рівна: C) 10. Диференціал y = B) 11. Частинна похідна D) 12. Точка рухається прямолінійно по закону S (t) = 4 et (м). Прискорення прямолінійного руху це: B) друга похідна від даного рівняння; 13. Диференціал функції експонентного розподілу F (x) = 1 – e-lx дорівнює: C) + le-lxdx;
14. Зміщення у відповідь на м’язове подразнення (одиничний імпульс) описується рівнянням y = kte -t /2. Як визначити швидкість процесу: A) знайти першу похідну від виразу; 15. Кількість речовини D) v
1. Похідна функції у = е–х рівна: B) – e-x;
2. Похідна функції у = ln х 2 рівна: B) 3. Коливання камертона проходить за законом х = 0,2 А × sin 800 π t. Швидкість коливання камертона знаходиться як: C) перша похідна від заданого рівняння по t;
4. У середовище вносять 1000 бактерій. Чисельність у бактерій зростає за такою залежністю: A) у¢ = 0 і визначивши t підставляємо у початкове рівняння отримаємо у;
5. Формула для диференціювання функції D) 6. Функція монотонно зростає, якщо: А) перша похідна > 0;
7. Похідна від складеної функції С) 8. Найменше значення функції В) 9. Диференціал від частки двох функцій C)
10. Частинна похідна C) 11. Диференціал функції у = f (x) виражається формулою: A)
12. Повний диференціал від функції z (x, y) = х 2+2 у 3 дорівнює: D) dz = 2 xdx+ 6 y2dy;
13. Залежність між кількістю х речовини, отриманої врезультаті хімічної реакції і часом t виражається рівнянням x (t) = c (1 – e-kt); k, c – const. Швидкість реакції дорівнює: D) cke-kt;
14. Диференціал функції у = ln (x 2 + 1) рівний: C) 15. Дріжджі ростуть у цукровому розчині, причому їх маса збільшується на 3 % за кожну годину. Якщо початкова маса становить 1 кг, то маса через А) 1. Похідна функції у =е2х – 1 рівна: D) 2 е2х – 1; 2. Похідна функції A) 0;
3. Перша похідна функції продукту хімічної реакції визначає: A) швидкість хімічної реакції;
4. Хворому роблять ін’єкцію в момент часу t = 0. Концентрація лікарського препарату в крові в момент t описується рівнянням x (t) = c (e-at – e - bt), a, b, c – const, a<b. Для визначення максимального значення концентрації ліків у крові в момент часу t: A) необхідно взяти першу похідну з даного рівняння, прирівняти до нуля і знайти значення t, а потім підставити у вихідне рівняння;
5. Формула диференціювання складеної функції А) Е) серед відповідей немає правильної.
6. Диференціал суми двох функцій С) 7. Найбільше значення функції D) 8. Частинна похідна А)
9. Частинна похідна функції двох змінних z = x 2 + 2 y 2 по змінній у рівна: C) 10. Похідна функції двох змінних z = ln (xy) по змінній х B) 11. Частинна похідна C)
12. Диференціал від константи с дорівнює: B) 0; 13. Повний диференціал від функції E) dz = y cos (xy) dx + x cos (xy) dy.
14. Диференціал першого порядку від функції у = 3 cos (x 2 + 1) становить: D) dy = –6 x sin (x 2+1) dx;
15. Розчинення лікарських речовин з таблеток підпорядковується рівнянню В) v
1. Похідна функції у = х 2+3 рівна: D) 2 х;
2. Похідна функції A) 3. Друга похідна від функції продукту хімічної реакції визначає: B) прискорення хімічної реакції; 4. Максимум функція
A) + на –;
5. Диференціал від частки двох функцій А) 6. Функція А) . 7. Зміщення у відповідь на м’язове подразнення одиничним імпульсом описується рівнянням А) знайти першу похідну;
8. Диференціал функції В)
9. Як знайти максимальну швидкість окиснення азоту, якщо рівняння кінетики має вид v = k (100 x 2 – x 3), де k – стала, х – концентрація окису азоту: D) необхідно з рівняння 10. Частинна похідна функції двох змінних z = exy по змінній х рівна: B) 11. Частинна похідна D)
12. Диференціал функції B) dy = 4sin 2 x×cos 2 xdx; 13. Повний диференціал використовують: C) для визначення граничної похибки посередніх вимірювань; В) 1;
14. Повний диференціал від функції двох змінних z (x, y) виражається формулою: D) 15. Частинна похідна С) У
1. Похідна функції C) 0;
2. Перша похідна функції фізично означає: A) швидкість процесу;
3. Похідна функції A) 4. Умовою спадання функції D)
5. Похідна функції D) 4 cos 4 x; 6. Форму комплексу потенціалів, яка виникає при збуджені сітківки ока світлом виражається рівнянням:
A) першою похідною від даного рівняння;
7. Формула для диференціювання функції С) 8. Похідна складеної функції А) 9. Найменше значення функції С)
10. Диференціал добутку двох функцій С) 11. Частинна похідна функції двох змінних C) 12. Відомо, що якщо полімерні молекули утворюються шляхом рекомбінації, то мольна доля у молекули полімеру з числом ланцюгів х має вид: B) знайти першу похідну і прирівняти її до нуля; 13. Диференціал функції D) 14. Повний диференціал функції A) 15. Частинна похідна А)
|
||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 630; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.167.10 (0.009 с.) |

 рівна:
рівна: .
.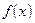 має, коли
має, коли  і при переході через точку змінює знак з:
і при переході через точку змінює знак з: визначається формулою:
визначається формулою: ;
; дорівнює:
дорівнює: ;
; на відрізку
на відрізку  дорівнює:
дорівнює: ;
; рівний:
рівний: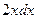 ;
; для функції: f (x, y) = x 3× y 2 рівна:
для функції: f (x, y) = x 3× y 2 рівна: ;
; , яка утворюється при хімічних реакціях другого порядку за час
, яка утворюється при хімічних реакціях другого порядку за час  , визначається за формулою:
, визначається за формулою:  . Якою формулою виразити швидкість реакції?
. Якою формулою виразити швидкість реакції? ;
; ;
; , де t – час. Максимальна кількість бактерій буде коли:
, де t – час. Максимальна кількість бактерій буде коли: виражається:
виражається: ;
; дорівнює:
дорівнює: ;
; на відрізку
на відрізку  дорівнює:
дорівнює: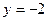 ;
;
 виражається формулою:
виражається формулою: ;
; ;
; ;
; ;
; .Як виразиться швидкість зміни
.Як виразиться швидкість зміни  ?
? ;
; рівна:
рівна: дорівнює:
дорівнює: ;
; рівний:
рівний: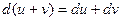 ;
; на проміжку
на проміжку  рівне:
рівне: ;
; від функції
від функції  рівна:
рівна: ;
;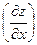 рівна:
рівна: ;
;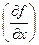 для функції
для функції  рівна:
рівна: є:
є: , де
, де  - кількість лікарської речовини в таблетці, яка залишилася до часу розчинення
- кількість лікарської речовини в таблетці, яка залишилася до часу розчинення  - вихідна кількість лікарської речовини в таблетці;
- вихідна кількість лікарської речовини в таблетці; 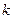 - постійна швидкості розчинення. Чому дорівнює швидкість розчинення лікарських речовин з таблеток?
- постійна швидкості розчинення. Чому дорівнює швидкість розчинення лікарських речовин з таблеток?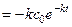 ;
; рівна:
рівна: ;
; визначається формулою:
визначається формулою: ;
; на відрізку
на відрізку  приймає найбільше значення:
приймає найбільше значення: ;
; ,
,  . Як визначити швидкість зміщення залежно від часу?
. Як визначити швидкість зміщення залежно від часу? виразиться формулою:
виразиться формулою: ;
; і знайти x і підставити у формулу;
і знайти x і підставити у формулу; ;
; рівна:
рівна: є:
є: ;
; функції
функції  дорівнює:
дорівнює: рівна:
рівна: рівна:
рівна: ;
; є:
є: < 0;
< 0; рівна:
рівна: , де r – стала, t – час. Швидкість зміни потенціалів визначається:
, де r – стала, t – час. Швидкість зміни потенціалів визначається: визначається:
визначається: ;
; дорівнює:
дорівнює: ;
; на відрізку
на відрізку 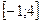 рівне:
рівне: дорівнює:
дорівнює: ;
; по змінній у рівна:
по змінній у рівна: ;
; . Для знаходження максимального розподілу по молекулярній масі потрібно спочатку:
. Для знаходження максимального розподілу по молекулярній масі потрібно спочатку: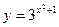 дорівнює:
дорівнює: ;
; дорівнює:
дорівнює: ;
; рівне:
рівне: ;
;


