Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування диференціального числення до дослідження функційСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Мета заняття Узагальнити й систематизувати знання з диференціального числення, а саме навчитися застосовувати знання з теми до дослідження функції та побудови графіків. Розвивати різні способи і прийоми мислення.
Студенти повинні знати: правила диференціювання; загальну схему дослідження функцій; необхідні й достатні умови зростання та спадання функції, існування точок екстремуму, інтервалів опуклості та точок перегину графіка функції; поняття асимптоти і її види.
Студенти повинні вміти: обчислювати похідні за формулами; застосовувати їх до дослідження функцій; будувати графіки функцій, для яких проведено повне дослідження. Основні питання теми Диференціальне числення застосовується до дослідження функції і побудови її графіка за загальною схемою: 1)Область визначення і множина значень функції: 2)Нулі функції 3)Властивості функції (парність або непарність, неперервність, обмеженість, періодичність) 4)Знаходження інтервалів монотонності функції та точок екстремуму функції 5)Знаходження інтервалів опуклості та точок перегину графіка функції 6)Асимптоти графіка функції 7)Побудова графіка 8)Приклади
Свої набуті знання ви можете перевірити в наступному тесті 1.Якщо диференційовна на інтервалі (а;b) функція спадає, то її похідна на цьому інтервалі... а)< 0 або = 0 б)> 0 або = 0 в)= 0 г)не існує 2.Точка, в якій похідна функції дорівнює нулю або не існує називається... а)точкою мінімуму б)точкою максимуму в)стаціонарною точкою г)точкою екстремуму 3.Значення функції в точці мінімуму називається... а)максимумом функції б)екстремумом функції в)мінімумом функції г)наближенням функції 4.Точка області визначення функції, яка одночас є кінцем двох інтервалів різної опуклості називається....... а)точкою неперервності функції б)точкою мінімуму функції в)точкою максимуму функції г)точкою перегину графіка функції 5.Якщо друга похідна функції f ''(х) на даному інтервалі > 0, то графік функції... а)опуклий донизу на даному інтервалі б)опуклий догори на даному інтервалі в)зростає на даному інтервалі г)спадає на даному інтервалі 6.Пряма, яка підходить до графіка функції дуже близько, але ніколи його не перетинає називається... а)асимптотою б)нормаллю в)дотичною г)січною 7.Асимптоти бувають.... а)похилі б)вертикальні в)горизонтальні г)хвилясті 8.Різниця двох значень аргументів функції називається... а)диференціалом функції б)прирістом функції в)прирістом аргументу г)похідною функції 9.Якщо а - точка розрива функції, то вертикальну асимптоту задає рівняння... а) у = в б) х = а в) у = а г) х = в 10.Графік функції у = f(х) буде опуклий догори на інтервалі (а;в), якщо на цьому інтервалі... а)похідна функції f ' (х) зростає б)похідна функції f ' (х) спадає в)похідна функції f ' (х) стала г)похідної функції f ' (х) не існує 11.Якщо похідна функції у=f '(х) < 0 на інтервалі (а;b), то функція на цьому інтервалі.. а)спадає б)стала в)зростає г)не існує 12.Якщо диференційовна на інтервалі (а;b) функція зростає, то її похідна на цьому інтервалі.. а)< 0 або = 0 б)> 0 або = 0 в)= 0 г)не існує 13.Точки мінімума і максимума функції називаються.......... а)точками екстремуму функції б)точками розрива функції в)точками неперервності функції г) стаціонарними точками функції 14.Значення функції в точці максимуму називається......... а)максимумом функції б)екстремумом функції в)мінімумом функції г)наближенням функції 15.Точки перегину графіка функції знаходяться за допомогою... а)асимптот графіка б)похідної першого порядку в)монотонності функції г)похідної другого порядку 16.Якщо друга похідна функції f ''(x) на даному інтервалі < 0, то графік функції............ а)опуклий донизу на даному інтервалі б)опуклий догори на даному інтервалі в)зростає на даному інтервалі г)спадає на даному інтервалі 17.Пряма, відстань від точок якої до точок графіка функції прямує до 0 називається... а)асимптотою б)нормаллю в)дотичною г)січною 18. Графік функції може мати вертикальні асимптоти х=а, якщо функція в точці а буде... а)неперервною б)сталою в)розривною г)дотичною 19.Рівняння у = кх + в може задавати таку асимптоту до графіка функції у = f(х)... а)похилу б)вертикальну в)горизонтальну г)хвилясту 20.Графік функції у = f(х) буде опуклий донизу на інтервалі (а;в), якщо на цьому інтервалі... а)похідна функції f ' (х) зростає б)похідна функції f ' (х) спадає в)похідна функції f ' (х) стала г)похідної функції f ' (х) не існує
Завдання для самоперевірки Дослідити функцію та побудувати її графік 1. 3. Знайти інтервали монотонності таких функцій: 1. 3. 5. 7. 9. 11. 13. Визначити екстремуми функцій: 1. 3. 5. 7. 9.
Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл.5, стор.246 – 266
Для більш глибокого вивчення теми рекомендовано обрати одну із запропонованих тем для написання реферату. Теми рефератів: 1.Застосування похідної в економіці. 2.Диференціювання функцій, заданих графічно і таблично. 3.Екстремальні задачі. Лекція „Загальний план дослідження функції” 1. Знайти область визначення та значення функції, заданої формулою, якщо таку область не зазначено. 2. Дослідити функцію на парність, непарність, періодичність. 3. З’ясувати точки перетину функції з вісями координат. 4. Дослідити функцію на неперервність. 5. Знайти асимптоти графіка функції (якщо вони існують). 6. З’ясувати, як функція поводиться на кінцях кожного з проміжків області визначення (знайти границі функції на кінцях цих проміжків, якщо вони є). 7. Дослідити функцію на диференційовність. 8. Дослідити функцію на монотонність та екстремуми. Знайти екстремуми і значення функції в точках екстремуму. 9. Дослідити функцію на опуклість (вгнутість): знайти інтервали опуклості (вгнутості), а також точки перегину функції. 10. Знайти найбільше і найменше значення функції (якщо вони існують). 11. Побудувати графік функції.
1. Функція не існує в точках
2. Функція непарна, оскільки Функція неперіодична. 3. Точки перетину з осями координат: з віссю Ох: (0; 0) — точка перетину з віссю Ох. з віссю Оу: (0; 0) — точка перетину з віссю Оу. 4. Функція невизначена в точці
Точки
5. Знаходимо асимптоти функції. Насамперед з’ясовуємо, що прямі Шукаємо похилу асимптоту
Отже, 6. В п. 4 знайдені односторонні границі функції в точках
7. Знайдемо першу похідну від функції у (вона існує на D (x)):
8. Дослідимо функцію на монотонність і знайдемо точки екстремуму. Для знаходження стаціонарних точок прирівнюємо першу похідну до нуля:
Зважаючи на зауваження п. 2, розглядатимемо дослідження функції при
Тому
9. Знайдемо другу похідну функції у:
Точка х = 0 може бути точкою перегину, бо
Друга похідна змінює в точці х = 0 свій знак, тому функція 10. Найбільше та найменше значення функції не існують. 11. Побудуємо графік функції, враховуючи дослідження.
Рис. 1 Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл.5, стор.246 – 266
Розділ”Диференційованість функцій багатьох змінних” Тема 16
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 490; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.100.40 (0.009 с.) |

 . 2.
. 2.  .
. .
. . 2.
. 2.  .
.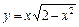 . 4.
. 4.  .
. 6.
6.  .
. . 8.
. 8.  .
. . 10.
. 10.  .
. . 12.
. 12.  .
. .
. . 2.
. 2.  .
. . 4.
. 4.  .
. . 6.
. 6.  .
. . 8.
. 8.  .
. . 10.
. 10. 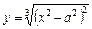 .
. Побудуємо графік функції
Побудуємо графік функції  .
. . Тому область визначення функції
. Тому область визначення функції
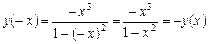 . З огляду на непарність функції достатньо побудувати її графік лише при
. З огляду на непарність функції достатньо побудувати її графік лише при  .
.

 тому ці точки є «підозрілими» на розрив. Знайдемо односторонні границі в точці
тому ці точки є «підозрілими» на розрив. Знайдемо односторонні границі в точці 

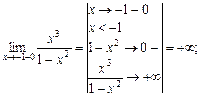

 — область неперервності функції.
— область неперервності функції.
 ;
; .
. — похила асимптота.
— похила асимптота. і
і 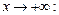







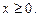

 , коли
, коли  ,
, , коли
, коли 
 — точка максимуму,
— точка максимуму,  — точка мінімуму.
— точка мінімуму.
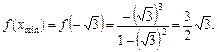
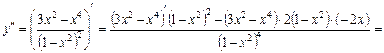

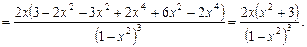
 Перевіримо це за критерієм. Визначимо знак
Перевіримо це за критерієм. Визначимо знак  в околі точки х = 0
в околі точки х = 0
 має точку перегину х = 0, на проміжку (0; 1) функція опукла, (1, +∞) — функція вгнута.
має точку перегину х = 0, на проміжку (0; 1) функція опукла, (1, +∞) — функція вгнута.