
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свої набуті знання ви можете перевірите в наступному тестіСодержание книги
Поиск на нашем сайте
1.Визначник, який утворюється з даного в результаті викреслення і-го рядка та j-го стовпця називається... а)алгебраїчним доповненням А(і,j) елемента а(i,j) б)детермінантом А(i,j) в)мінором М(i,j) елемента а(i,j) г)матрицею А 2.Якщо мінор елемента береться зі знаком(-1) у степені(i+j),то він називається... а)алгебоаїчним доповненням А(i,j) елемента а(i,j) б)детермінантом А(i,j) в)мінором М(i,j) елемента а(i,j) г)матрицею А 3.Прямокутна таблиця чисел, що складається з m рядків та n стовпців називається... а)алгебраїчним доповненням А(i,j) елемента а(i,j) б)детермінантом порядку i наj в)мінором М(i,j) елемента а(і,j) г)матрицею порядка m на n 4.Матриця, в якій число рядків дорівнює числу стовпців, називається... а)квадратною б)діагональною в)одиничною г)нульовою 5.Якщо всі елементи матриці дорівнюють 0, то вона називається... а)квадратною б)діагональною в)одиничною г)нульовою 6.Якщо всі елементи квадратної матриці, крім тих, що стоять на головній діагоналі, дорівнюють 0, то матриця називається... а)квадратною б)діагональною в)одиничною г)нульовою 7.Діагональна матриця, у якої кожен елемент головної діагоналі дорівнює 1, називається... а)квадратною б)діагональною в)одиничною г)нульовою 8.Якщо кількість стовпців матриці А дорівнює кількості рядків матриці В, то матриця А називається...... до матриці В а)протилежною б)невиродженою в)виродженою г)узгодженою 9.Якщо визначник матриці дорівнює нулю, то вона називається... а)протилежною б)невиродженою в)виродженою г)узгодженою 10.Якщо визначник матриці не дорівнює нулю, то вона називається... а)протилежною б)невиродженою в)виродженою г)неузгодженою 11.Найбільший з порядків мінорів матриці А, що не дорівнює нулю, називається... а)визначником матриці А б)рангом матриці А в)алгебраїчним доповненням матриці А г)множником матриці А 12.Система лінійних рівнянь, що має 3 змінних і 3 рівняння має едине рішення, якщо головний визначник системи... а)не дорівнює 0 б)дорівнює 0 в)не існує г)дорівнює рангу системи 13.Матриця А має обернену тоді і тільки тоді, коли вона є... а)виродженою б)невиродженою в)нульовою г)узгодженою
Завдання для самоперевірки Обчислити ранг наступних матриць
Відповідь. r = 2. Відповідь. r = 3.
Відповідь. r = 2. Відповідь. r = 2.
Відповідь. r = 3. Відповідь. r = 3.
Відповідь. r = 4. Відповідь. r = 3.
Відповідь. r = 2. Відповідь. r = 3.
Відповідь. r = 6. Відповідь. r = 5.
Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001, стор.18 – 19, 30 – 31.
Для більш глибокого вивчення теми рекомендовано обрати одну із запропонованих тем для написання реферату. Теми рефератів: 1.Матричне числення (приклади з економіки) 2.Історія розвитку лінійної алгебри.
Лекція „Ранг матриці” Створено багато методів і способів розв’язування системи лінійних алгебраїчних рівнянь. Розглянемо найважливіші з них, що спираються на поняття рангу матриці. Означення. Рангом матриці А називається ранг її векторів-стовпців. Отже, рангом матриці можна назвати найбільше число лінійно незалежних її стовпців. Далі за допомогою теорії визначників буде доведено, що ранг матриці дорівнює також найбільшому числу лінійно незалежних її рядків. Із теореми 6, наведеної в підрозд. 2.1.3, випливає така теорема. Теорема 1. Ранг матриці не змінюється в результаті еквівалентних перетворень стовпців або рядків матриці. За допомогою еквівалентних перетворень досягають того, щоб якомога більше елементів матриці дорівнювали нулю. Для обчислення рангу матриці користуються наведеною далі теоремою. Теорема 2. Нехай у матриці А в кожному рядку і кожному стовпці міститься не більш як один ненульовий елемент. Тоді Доведення теореми випливає з того, що стовпці матриці, які містять ненульові елементи, будуть лінійно незалежні. ¨
· Помножимо перший рядок на 2 і віднімемо від другого рядка. Далі помножимо перший рядок на 3 і віднімемо від третього рядка. У результаті дістанемо еквівалентну матрицю:
Віднявши другий рядок від третього, запишемо матрицю
Обчислення рангу матриці на цьому етапі можна припинити, оскільки матриця А 2 має лише два ненульові рядки. Звідси випливає, що ранг матриці А 2 не може бути більшим за два. Крім того, матриця А 2 має два ненульові лінійно незалежні рядки. Отже, Продовжимо еквівалентні перетворення матриці А 2. Помножимо перший стовпець на 2 і віднімемо від другого стовпця, далі додамо перший стовпець до третього, помножимо перший стовпець на 3 і віднімемо від четвертого стовпця. Зрештою дістанемо матрицю
Помножимо другий її стовпець на 4 і віднімемо від третього стовпця, далі помножимо другий стовпець на 5 і додамо до четвертого стовпця. У результаті утвориться матриця
яка в кожному рядку і кожному стовпці має не більш як один ненульовий елемент. Таким чином, Перейдемо до розгляду систем лінійних алгебраїчних рівнянь. Їх розв’язування зводиться до виконання еквівалентних (тобто таких, що не змінюють розв’язків) перетворень системи рівнянь. А саме, можна переставляти рівняння, множити рівняння на числа, відмінні від нуля, і додавати до одного рівняння інше, помножене на деяке число. Означення. Якщо система лінійних рівнянь має розв’язки, то вона називається сумісною. Якщо система рівнянь не має розв’язків, то вона називається несумісною, або суперечливою. Якщо розв’язок системи єдиний, то система називається визначеною. Якщо система має більш як один розв’язок, її називають невизначеною.
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.66.147 (0.01 с.) |

 .
.  .
. .
.  .
.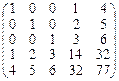 .
. 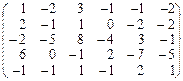 .
. .
.  .
. .
.  .
. .
. 
 дорівнює загальному числу всіх ненульових елементів матриці А.
дорівнює загальному числу всіх ненульових елементів матриці А. Знайдемо ранг матриці
Знайдемо ранг матриці .
. .
. .
. .
.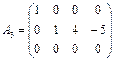 .
.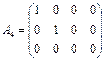 ,
, .
.


