
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначає пучок прямих, які проходять через точку перетину прямих (1). Вибором l можна дістати будь-яку пряму, що проходить через точку перетину прямих (1), крім другої прямої.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Доведення. При кожному значенні l рівняння (5), що є лінійним, визначає деяку пряму. Припустимо, що коефіцієнти при х, у перетворюються на нуль:
Тоді виконується рівність
а це означає, що прямі (1) паралельні. Нехай М 0(х 0, у 0) є точкою перетину прямих (1):
Звідси випливає, що
тобто пряма (5) проходить через точку М 0(х 0, у 0). Візьмемо тепер довільну точку площини М 1(х 1, у 1) і виберемо l так, щоб пряма (5) проходила через точку М 1. Для цього має виконуватися рівність
з якої завжди можна визначити l за умови
Іншими словами, точка М 1 не повинна лежати на другій прямій (1). Отже, і справді вибором параметра l можна дістати будь-яку пряму, що проходить через точку перетину прямих (1), за винятком другої прямої (1). Теорему доведено. ¨
Знайдемо рівняння його висоти, проведеної з вершини С. ● Складемо рівняння пучка променів, які проходять через вершину С:
Далі за умовою (3) перпендикулярності прямих до АВ маємо:
Звідси знаходимо значення l = 4 і рівняння висоти 2 х + у – 7 = 0. · Відстань від точки до прямої Дано загальне рівняння прямої Ах + Ву + С = 0 (1) і точку М 1(х 1, у 1). Знайдемо відстань d від точки М 1 до прямої (1). Візьмемо точку М 0(х 0, у 0) на цій прямій. Тоді відстань від точки М 1 до прямої дорівнює проекції вектора
Рис. 4
Записуємо аналітичний вираз для шуканої відстані:
Оскільки – Ах 0 – Ву 0 = С, то остаточно маємо:
Означення. Рівняння виду
називається нормальним рівнянням прямої (1). Знак перед радикалом має бути протилежний знаку вільного члена С. Якщо Узявши в нормальному рівнянні (3)
запишемо його у вигляді
де q — кут між віссю х і вектором нормалі n; р — відстань від прямої до початку координат (рис. 5).
Рис. 5 Перейдемо до полярних координат, скориставшись рівностями х = r cosj, у = r sinj. Тоді нормальне рівняння прямої набере вигляду
Залежність, записану формулою (2), можна сформулювати як теорему. Теорема 3. Для того щоб знайти відстань d від точки
· За формулою (2) знаходимо
Нехай маємо загальні рівняння двох прямих, що перетинаються:
Якщо точка М (х, у) лежить на бісектрисі кутів, утворених прямими (4), то вона однаково віддалена від цих прямих, тобто виконується рівність:
Рис. 6
● Згідно з (5) записуємо рівняння двох бісектрис:
Звідси маємо:
Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл.3, §7, стор.80.
Тема 7 Кут між двома площинами. Умови паралельності та перпендикулярності двох площин. Відстань від точки до площини
Мета заняття Навчитися розв'язувати задачі, користуючись умовами || та ┴ площин, формулою кута між двома площинами та відстані від точки до площини. Розвивати просторове мислення.
Студенти повинні знати: формули обчислення кута між двома площинами, умови перпендикулярності та паралельності двох площин, формулу відстані від точки до площини. Студенти повинні вміти: розв'язувати задачі на формули та умови паралельності та перпендикулярності двох площин, знаходити відстань від точки до площини; Основні питання теми 1.Визначення кута між двома прямими; 2.Умови паралельності двох прямих; 3.Умови перпендикулярності двох прямих; 4.Знаходження відстані від точки до площини; 5.Розвязування задач з теми
Завдання для самоперевірки 1.Записати та дослідити загальне рівняння площини. 2.Вивести рівняння площини, яка проходить через три точки. 3.Вивести рівняння площини у відрізках на осях. 4.Задано точки А(1;2;-1) і В(0;3;1). Скласти рівняння площини, яка проходить через точку А перпендикулярно до вектора АВ. 5.Знайти відстань між площинами 2х – у + 2z + 9 = 0 і 4х – 2у + 4z – 21 = 0. Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 Гл. 3, стор. 87 – 88. Лекція ”Відстань від точки до площини” Дано площину
і точку М 1(х 1, у 1, z 1) поза нею. Знайдемо відстань від точки М 1 до площини. Нехай точка М 0(х 0, у 0, z 0) лежить на площині. Тоді відстань d від точки М 1 до площини дорівнює модулю проекції вектора
Рис. 2 Отже,
Оскільки
то
· Згідно з (1) маємо:
Рівняння площини, записане у вигляді
де знак перед радикалом протилежний знаку D, називається нормальним рівнянням площини. Якщо D = 0, то вибір знака неістотний. Щоб знайти відстань від точки М 1(х 1, у 1, z 1) до площини, слід підставити координати цієї точки в нормальне рівняння площини і знайти модуль здобутої величини. Величина
називається відхиленням точки М(х, у, z) від площини. Модуль відхилення дорівнює відстані від точки М ( х, у, z ) до площини. Якщо Коли маємо дві площини, які перетинаються й подаються рівняннями
то бісектральні площини визначаються рівнянням
Взаємне розміщення двох площин Нехай дано дві площини, які визначаються загальними рівняннями
Розглянемо вектори нормалей до кожної з площин:
Кут q між площинами визначається кутом q між векторами
Умова перпендикулярності площин така:
Умова паралельності площин:
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.122.95 (0.01 с.) |






 .
. Маємо рівняння сторін трикутника:
Маємо рівняння сторін трикутника:
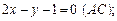



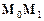 на вектор нормалі
на вектор нормалі  (рис. 4).
(рис. 4).
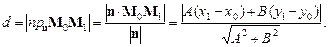
 (2)
(2) (3)
(3)



 ·
· (4)
(4) . (5)
. (5)

 (6)
(6)
 , на нормаль до площини (рис. 2).
, на нормаль до площини (рис. 2).
 .
.
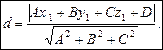 (1)
(1)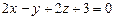 .
. . ·
. ·

 , то точка М ( х, у, z ) і початок координат лежать по один бік від розглядуваної площини; якщо
, то точка М ( х, у, z ) і початок координат лежать по один бік від розглядуваної площини; якщо 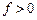 , — по різні боки; якщо
, — по різні боки; якщо 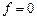 , то М лежить на цій площині.
, то М лежить на цій площині.
 (2)
(2) .
.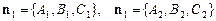 .
. . Отже, справджується рівність
. Отже, справджується рівність . (1)
. (1) . (2)
. (2) . (3)
. (3)


