
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пряма. Взаємне положення прямихСодержание книги Поиск на нашем сайте
Рисунок 1.5 – Утворення прямокутних проекцій прямої лінії
Відносно площин проекцій пряма може займати різне положення. Пряма, яка не паралельна жодній з площин проекцій має назву прямої загального положення. Комплексне креслення такої прямої показано на рис. 1.6. Пряму, паралельну одній з площин проекцій, називають прямою рівня. Пряму, перпендикулярну до однієї із площин проекцій, називають проекціювальною прямою.
Рисунок 1.6 - Комплексне креслення прямої загального положення
Точки, в яких пряма перетинає площини проекцій, називають слідами. На рис. 1.7 показано пряму загального положення, яка утворена двома точками N і M, кожна з яких належить відповідній площині проекцій. Тому сліди прямої лінії можна розглядати як точки, які одночасно належать прямій та площині проекцій.
Рисунок 1.7 - Сліди прямої загального положення
Пряма загального положення перетинає три площини проекцій, тому має три сліди. Пряма рівня перетинає дві площини проекцій. На рис. 1.8 показано побудову слідів горизонтальної прямої АВ. Точка M (M1,M2) – фронтальний слід прямої, точка N (N1,N3)- профільний слід прямої.
Рисунок 1.8 - Сліди прямої рівня Проекціювальна пряма перетинає одну площину проекцій. На рис.1.9 показано побудову сліду фронтально-проекціювальної прямої АВ. Точка M (M1,M2) – фронтальний слід прямої АВ, або точка, яка одночасно належить площині проекції Π2 та прямій.
Рисунок 1.9 - Слід проекціювальної прямої
Дві прямі в просторі можуть перетинатись, бути паралельними та мимобіжними.
Якщо дві прямі a і b перетинаються в деякій точці А (показано на рис. 1.10), то проекції цієї точки повинні належати однойменним проекціям прямих, тобто точки перетину однойменних проекцій прямих, що перетинаються, повинні належати одній лінії зв’язку А1А2.
Рисунок 1.10 - Утворення прямокутних проекцій прямих, що перетинаються Якщо дві прямі a і b паралельні (показано на рис. 1.11), то на комплексному кресленні їх однойменні проекції також паралельні a2//b2, a1//b1.
Рисунок 1.11 - Утворення прямокутних проекцій паралельних прямих
Рисунок 1.12 - Утворення прямокутних проекцій мимобіжних прямих
Задачі для самостійного розв’язування Задача №8 Побудувати проекції відрізків прямих АВ, CD, …, ST за заданими координатами вершин. Визначити положення прямих відносно системи площин проекцій.
Приклад розв’язування:
1-й крок 2-й крок
Прямокутні проекції відрізка АВ утворені шляхом сполучення побудованих на попередніх кроках однойменних прямокутних проекцій його окремих точок.
Задача №9 Визначити на заданих прямих точку М, що належить площині проекцій Π1, та точку N, що належить площині проекцій Π2.
а) б) в) Приклад типового розв’язування:
Задача №10 Побудувати прямокутні проекції прямих ℓ і m, які перетинаються в т. А. Пряма ℓ - фронталь, пряма m – профільна пряма.
Задача №11 Прямі h (горизонталь) та ℓ (загального положення) перетинаються під кутом 90°. Побудувати прямокутні проекції прямих.
Задача №12
Задача №13
Через точку В провести пряму ℓ, мимобіжну відносно прямої a. Пряма ℓ повинна проходити над прямою a.
Задача №14
Побудувати проекції фронталі f, яка знаходиться на відстані 20 мм від площини проекцій Π2 і перетинає задані паралельні прямі.
Задача №15
- CM – висота рівнобедреного трикутника; - точка А – належить площині проекцій Π1; - точка В – належить площині проекцій Π2
Задача №16 Через точку М провести пряму b, яка перетинає пряму a та вісь OZ.
Задача №17
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 602; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.221.252 (0.006 с.) |

 Відомо, що пряма лінія ℓ в просторі визначається положенням двох її точок, наприклад А і В, які показані на рис. 1.5. Це означає, що достатньо виконати комплексне креслення вказаних точок, з’єднати однойменні проекції точок прямими лініями та отримати відповідно горизонтальну А1В1, фронтальну А2В2, профільну А3В3 проекції прямої, заданої відрізком AB (див. рис. 1.5).
Відомо, що пряма лінія ℓ в просторі визначається положенням двох її точок, наприклад А і В, які показані на рис. 1.5. Це означає, що достатньо виконати комплексне креслення вказаних точок, з’єднати однойменні проекції точок прямими лініями та отримати відповідно горизонтальну А1В1, фронтальну А2В2, профільну А3В3 проекції прямої, заданої відрізком AB (див. рис. 1.5).









 Якщо дві прямі a і b мимобіжні, то на комплексному кресленні їх однойменні проекції перетинаються в точках, що не належать одній лінії зв’язку. На рис. 1.12 горизонтальні проекції прямих а1 і b1 перетинаються в точці А1=В1, яка відповідає горизонтальній проекції двох конкуруючих відносно площини проекцій Π1 точок А і В, а фронтальні проекції прямих а2 і b2 перетинаються в точці C2=D2, яка відповідає фронтальній проекції двох конкуруючих відносно площини проекцій Π2 точок C і D.
Якщо дві прямі a і b мимобіжні, то на комплексному кресленні їх однойменні проекції перетинаються в точках, що не належать одній лінії зв’язку. На рис. 1.12 горизонтальні проекції прямих а1 і b1 перетинаються в точці А1=В1, яка відповідає горизонтальній проекції двох конкуруючих відносно площини проекцій Π1 точок А і В, а фронтальні проекції прямих а2 і b2 перетинаються в точці C2=D2, яка відповідає фронтальній проекції двох конкуруючих відносно площини проекцій Π2 точок C і D.

 3-й крок
3-й крок
 Прямокутні проекції М1 і М2 шуканої точки M визначені за умови їх належності однойменним проекціям прямої f та урахуванням нульового значення координати Z.
Прямокутні проекції М1 і М2 шуканої точки M визначені за умови їх належності однойменним проекціям прямої f та урахуванням нульового значення координати Z.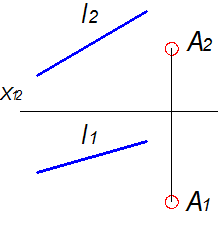 Побудувати проекції прямої m, яка проходить через т. А та паралельна прямій ℓ. Побудувати проекції горизонталі h, яка перетинає лінію ℓ.
Побудувати проекції прямої m, яка проходить через т. А та паралельна прямій ℓ. Побудувати проекції горизонталі h, яка перетинає лінію ℓ.

 Побудувати проекції Δ ACB, якщо:
Побудувати проекції Δ ACB, якщо: За заданими слідами A і P прямої m побудувати її проекції.
За заданими слідами A і P прямої m побудувати її проекції.


