Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольний тест до інформаційного модуля 4Содержание книги
Поиск на нашем сайте
1. Скільки додаткових площин проекцій необхідно ввести для визначення довжини відрізка прямої загального положення? а) одну; б) дві; в) три. 2. Оберіть правильний варіант розв’язування задачі на переведення прямої АВ із загального в проекціювальне положення:
а) б) в) 3. Скільки додаткових площин проекцій необхідно для приведення плоскої фігури загального положення в проекціювальне? а) одну; б) дві; в) три. 4. Оберіть правильний варіант введення додаткової площини для переведення площини, заданої ΔАВС в проекцію вальне положення.
а) б) в)
5. Оберіть правильний варіант визначення відстані між точкою та прямою
а) б) в) 6. а) одне; б) два; в) три.
7. Скільки переміщень треба зробити для перетворення площини α(АВС) в площину рівня?
а) одне; б) два; в) три. 8. Для визначення відстані між точкою С та площиною β(a║b) необхідно таке перше перетворення:
перпендикулярно X 1,2; б) a1║b1 перемістити перпендикулярно X 1,2; в) a2║b2 перемістити паралельно X 1,2.
ІНФОРМАЦІЙНИЙ МОДУЛЬ 5 КРИВІ ПОВЕРХНІ
Загальна характеристика формоутворення кривих ліній та кривих поверхонь Крива лінія – це геометричне місце послідовних положень точки, що здійснює неперервний рух в просторі. При утворенні кривої лінії у такий спосіб її можна подати у вигляді множини точок, які їй належать, і відобразити на комплексному кресленні як сукупність відповідних проекцій окремих точок множини, що показано на рис. 5.1.
Рисунок 5.1 - Комплексне креслення кривої лінії
Закон переміщення твірної зручно задавати деякими сталими лініями, що мають назву напрямних ліній.
Рисунок 5.2 – Каркас кривої поверхні
Кожна точка твірної при її русі описує деяку лінію m, сукупність яких складає також однопараметричну множину {m} (див. рис. 5.2). З кривих ℓ i та m i складається так званий сітчастий каркас кінематичної поверхні. Якщо врахувати неперервне переміщення твірної, а відповідно, неперервність і самої поверхні, то можна зробити висновок: через будь-яку точку М поверхні можна провести пару кривих ℓ м і m м. Сукупність умов, необхідних і достатніх для задання поверхні, називається визначником поверхні. Останній складається з геометричної та алгоритмічної частин. Геометричною частиною визначника поверхні є геометричні фігури, які беруть участь в утворенні поверхні. Алгоритмічна частина – це сукупність правил застосування геометричної частини визначника для утворення поверхні. Велика кількість різноманітних поверхонь, які використовують в інженерній практиці, потребує їх систематизації. Це особливо важливо в автоматизованому проектуванні при створенні інформаційних систем. В кінематичному способі утворення поверхонь цілком природно в основу систематизації покласти форму твірної лінії і закон її переміщення. Тому за формою твірної розрізняють лінійчаті (твірна – пряма), криволінійні (твірна – крива), за законом переміщення твірної – поверхні обертання, поверхні переносу і гвинтові.
Поверхні обертання Поверхні, утворені обертанням твірної лінії ℓ навколо нерухомої осі i, називаються поверхнями обертання (рис. 5.3). Геометрична частина визначника поверхні обертання – її вісь та одна твірна. Точки твірної A, B, C, D, E описують кола навколо осі. Ці кола знаходяться в паралельних між собою площинах і називаються паралелями. Найбільше і найменше з цих кіл отримали спеціальні назви – екватор і горло. Площини, що проходять через вісь обертання, називають меридіональними, а лінії по яких вони перерізають поверхню – меридіанами. Площину, яка паралельна до фронтальної площини проекцій, називають головною меридіональною площиною, а лінію її перерізу з поверхнею обертання – головним меридіаном. Визначник поверхні обертання буде мати вигляд:
Defθ = (ℓ, i) [A], де (ℓ, i) – геометрична частина визначника, яка складається з твірної ℓ та осі обертання i; [ A ] - алгоритмічна частина визначника, яка містить умову, що твірна ℓ обертається навколо осі i.
Рисунок 5.3 - Геометричні характеристики поверхні обертання
Найпростішими прикладами поверхонь обертання є конус, циліндр, сфера, тор. Зображеннями поверхонь обертання на площинах проекцій є так звані обриси. При паралельному проекціюванні довільної поверхні Φ на площину проекцій Πί деякі проекціювальні прямі будуть дотикатись поверхні Φ і утворювати проекціювальну циліндричну поверхню θ (рис. 5.4). Лінія дотику поверхонь θ і Φ (k), котра може бути просторовою або плоскою кривою, називається контурною лінією, а її проекція ki на площині Πί – обрисом даної поверхні Φ.
Рисунок 5.4 - Утворення обрисів поверхонь Якщо вісь обертання довільної поверхні займає проекціювальне положення відносно однієї площини проекцій, то обрисові лінії такої поверхні на дві інші площини проекцій будуть мати форму ідентичну формі головного меридіана. Для створення графічної моделі будь-якої поверхні обертання у вигляді її обрисів за заданими проекціями геометричної частини її визначника достатньо побудувати сукупність паралелей, яку утворює множина точок твірної. Послідовність виконання графічних операцій з побудови графічної моделі поверхні обертання довільного виглядунаведена нижче:
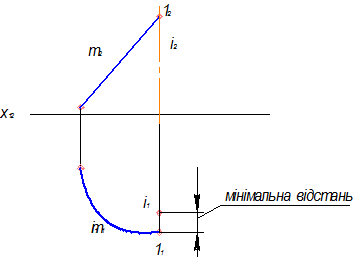
1. Визначаємо на твірній m точку, що знаходиться на мінімальній відстані від осі i. Для заданої твірної це буде точка 1 (11,12).
2. Будуємо проекції паралелі (горла), яку утворює внаслідок обертання навколо осі і точка 1.
3. Визначаємо на твірній m точку, що знаходиться на максимальній відстані від осі і. Для заданої твірної це буде точка 2 (21,22). Така точка внаслідок обертання утворить паралель, що матиме назву екватора.
4. Визначаємо на твірній декілька точок та будуємо відповідні проміжні паралелі, які утворюють визначені точки. До таких точок перш за все відноситься точка 3 (31,32).
5. З’єднаємо плавною кривою лінією крайні точки побудованих паралелей, отримуючи таким чином обрис поверхні обертання на фронтальній площині, або головний меридіан. На горизонтальній площині проекцій обрисовими лініями такої поверхні є проекції у вигляді кіл горла та екватора.
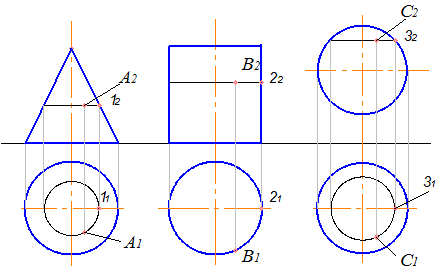
Розв’язання будь-якої позиційної задачі з використанням поверхні обертання вимагає знання алгоритму побудови проекцій точок, що належать цим поверхням. Такий алгоритм базується на побудові відповідних проекцій паралелей (або твірних, якщо поверхня лінійчата), на яких знаходиться та чи інша точка. Графічна інтерпретація алгоритму побудови наведена на рис. 5.5.
Рисунок 5.5 - Побудова точок на поверхнях обертання
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.194.30 (0.009 с.) |




 Скільки переміщень треба зробити для перетворення прямої АВ в пряму рівня?
Скільки переміщень треба зробити для перетворення прямої АВ в пряму рівня?
 а) a2║b2 перемістити
а) a2║b2 перемістити

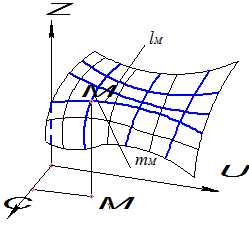 Криву поверхню можна розглядати як траєкторію переміщення деякої лінії (твірної), що здійснює неперервний рух в просторі. Деякі поверхні утворюються внаслідок руху лінії постійної форми, інші так, що твірна разом зі зміною положення в просторі змінює також і свою форму. Поверхню, показану на рис. 5.2, у такому випадку розглядають як однопараметричну множину твірних {ℓ}.
Криву поверхню можна розглядати як траєкторію переміщення деякої лінії (твірної), що здійснює неперервний рух в просторі. Деякі поверхні утворюються внаслідок руху лінії постійної форми, інші так, що твірна разом зі зміною положення в просторі змінює також і свою форму. Поверхню, показану на рис. 5.2, у такому випадку розглядають як однопараметричну множину твірних {ℓ}.

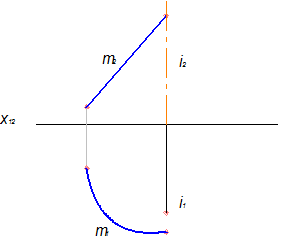 Дано:
Дано: