
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Паралельність прямих, прямої і площини, двох площин у просторіСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
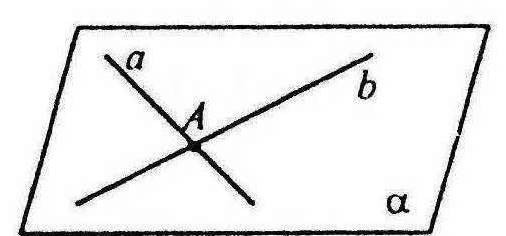
2.2.1 Дві прямі перетинаються, якщо вони мають єдину спільну точку (такі прямі лежать в одній площині).
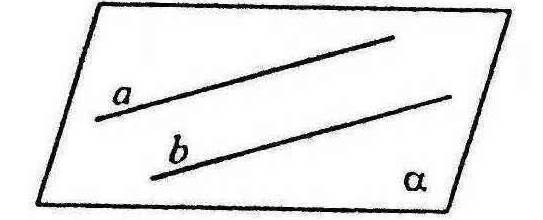
2.2.2 Дві прямі у просторі називаються паралельними, якщо вони лежать в одній площині і не перетинаються.
2.2.3 Прямі, які не перетинаються і не лежать в одній площині, називаються мимобіжними.
2.2.4
2.2.5 Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині.
2.2.6
2.2.7
2.2.8 Ознака паралельності площин
Властивості паралельних площин 2.2.9
2.2.10 Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну.
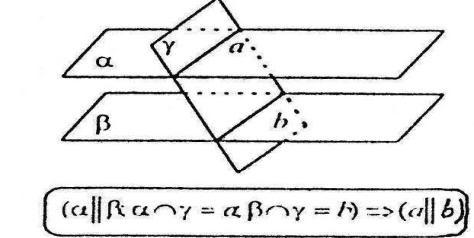
2.2.11 Якщо дві паралельні площини перетинаються третьою, то прямі перетину паралельні.
2.2.12
Зображення просторових фігур на площині
Властивості зображення фігур на площині
Проектування трикутників
При проектуванні будь-якого трикутника (гострого, тупокутного, прямокутного, рівнобедреного або рівностороннього) утворюється трикутник довільної форми (гострокутний чи тупокутний).
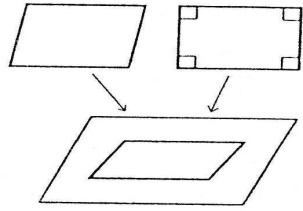
Проектування паралелограмів
Оскільки паралельність відрізків при проектуванні зберігається, паралелограми (а також прямокутники та квадрати) зображуються паралелограмами довільної форми.
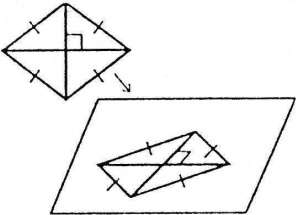
При проектуванні ромба незмінною стає одна з діагоналей,
Проектування трапеції
При проектуванні будь-яка трапеція (довільна, рівнобічна, прямокутна) зображується як довільна трапеція.
Проектування кола Коло при проектуванні на площину зображується як еліпс.
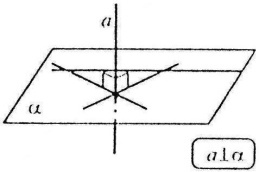
Перпендикулярність прямих і площин Пряма, яка перетинає площину, називається перпендикулярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині.
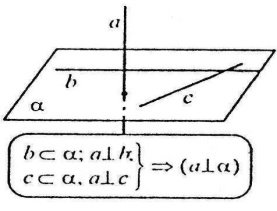
Ознака перпендикулярності прямої і площини Якщо пряма перпендикулярна до двох прямих, які лежать у площині і перетинаються, то вона перпендикулярна до даної площини.
Властивості прямої і площини, перпендикулярних між собою
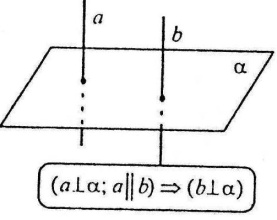
Дві прямі, перпендикулярні до однієї і тієї ж площини – паралельні.
Перпендикуляр і похила
Перпендикуляром, опущеним з даної точки на дану площину, називається відрізок, що сполучає дану точку з точкою площини (основою перпендикуляра) і лежить на прямій, перпендикулярній до площини; при цьому довжина перпендикуляра називається відстанню від даної точки до даної площини.
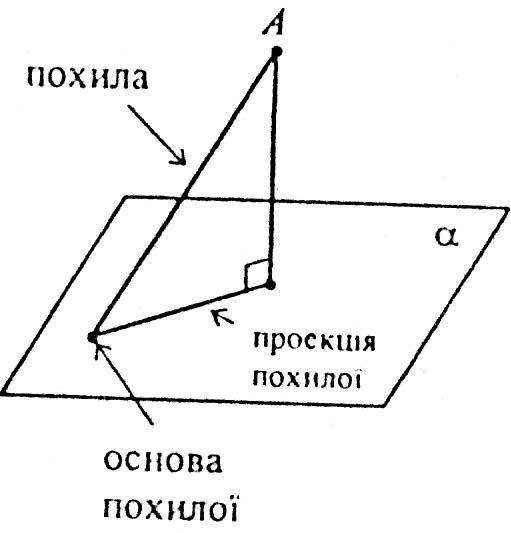
Похилою, проведеної з даної точки до даної площини, називається будь-який відрізок, який сполучає дану точку з точкою площини (основою похилої) і не є перпендикуляром до площини; відрізок, який сполучає основу перпендикуляра і похилої, проведених з однієї точки, називається проекцією похилої.
Рівні перпендикуляри, проведені з однієї точки поза площиною до цієї площини, мають рівні проекції. Якщо дві похилі, проведені з однієї точки поза площиною до цієї площини, мають рівні проекції, то вони рівні.
Найбільша з двох похилих, проведених з однієї точки поза площиною до цієї площини, що має більшу проекцію, більша.
Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до її похилої. І навпаки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.
Перпендикулярність площин
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 993; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.166.45 (0.009 с.) |


 Пряма і площина називаються паралельними, якщо вони не перетинаються.
Пряма і площина називаються паралельними, якщо вони не перетинаються.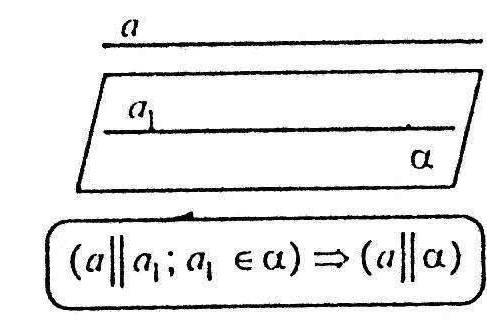 Ознака паралельності прямої і площини
Ознака паралельності прямої і площини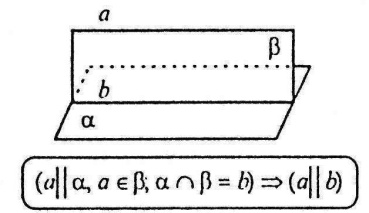 Якщо через пряму, яка паралельна даній площині, проходить площина, що перетинає дану площину, то пряма, за якої перетинаються ці площини, буду паралельна даній прямій.
Якщо через пряму, яка паралельна даній площині, проходить площина, що перетинає дану площину, то пряма, за якої перетинаються ці площини, буду паралельна даній прямій. Дві площини називаються паралельними, якщо вони не перетинаються.
Дві площини називаються паралельними, якщо вони не перетинаються.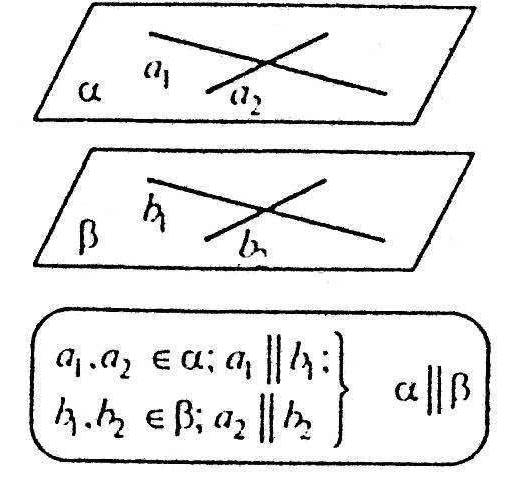 Якщо дві прямі, які перетинаються, однієї площини відповідно паралельні двом прямим другої площини, то ці площини паралельні.
Якщо дві прямі, які перетинаються, однієї площини відповідно паралельні двом прямим другої площини, то ці площини паралельні.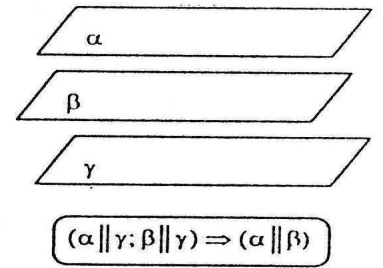 Дві різні площини, які паралельні третій, паралельні.
Дві різні площини, які паралельні третій, паралельні.
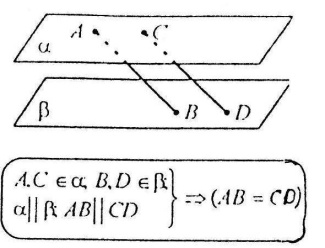 Відрізки паралельних прямих, які містяться між двома паралельними площинами – рівні.
Відрізки паралельних прямих, які містяться між двома паралельними площинами – рівні. Для зображення просторових фігур на площині користуються паралельним проектуванням: такий спосіб відповідає зоровому сприйманню фігури під час їх розглядання здалеку.
Для зображення просторових фігур на площині користуються паралельним проектуванням: такий спосіб відповідає зоровому сприйманню фігури під час їх розглядання здалеку.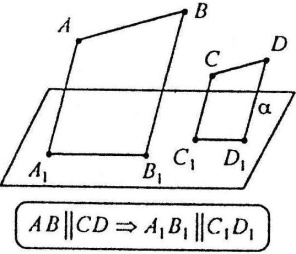 Прямолінійні відрізки фігури зображуються на площині малюнка відрізками; паралельні відрізки фігури зображуються на площині малюнка паралельними відрізками.
Прямолінійні відрізки фігури зображуються на площині малюнка відрізками; паралельні відрізки фігури зображуються на площині малюнка паралельними відрізками.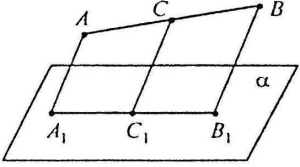 Середина відрізка при зображенні його на площині теж є серединою.
Середина відрізка при зображенні його на площині теж є серединою.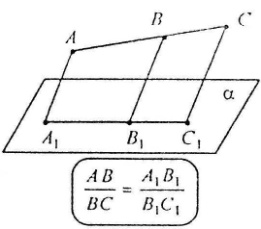 Відношення відрізків однієї прямої або паралельних прямих збігається при паралельному проектуванні.
Відношення відрізків однієї прямої або паралельних прямих збігається при паралельному проектуванні.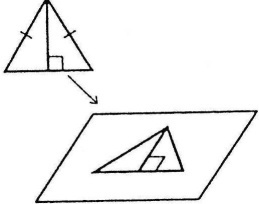

 проекцією є паралелограм.
проекцією є паралелограм.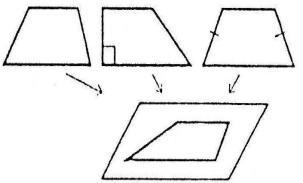
 Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої.
Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна й до другої.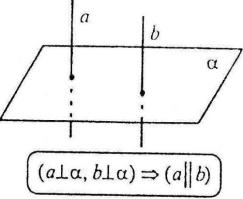
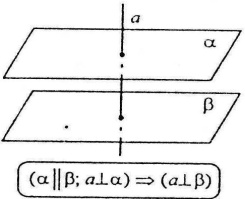 Пряма, яка перпендикулярна одній із двох паралельних площин, перпендикулярна й до другої.
Пряма, яка перпендикулярна одній із двох паралельних площин, перпендикулярна й до другої. Якщо пряма перпендикулярна до двох різних площин, то ці площини паралельні.
Якщо пряма перпендикулярна до двох різних площин, то ці площини паралельні.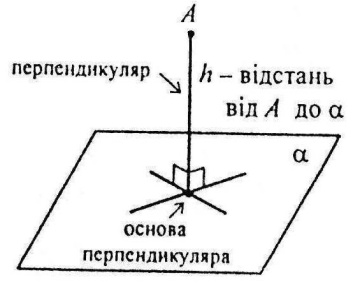
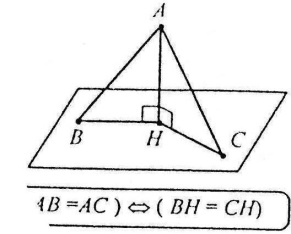 Властивості перпендикулярів і похилих
Властивості перпендикулярів і похилих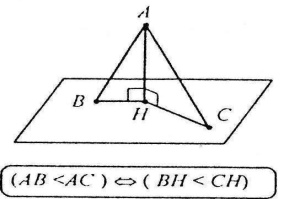
 Теорема про три перпендикуляри
Теорема про три перпендикуляри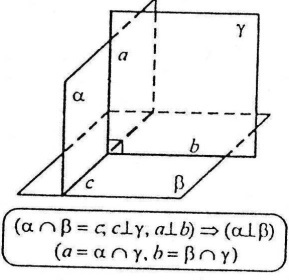 Дві площини, що перетинаються, називаються перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину цих площин, перетинає їх по перпендикулярним прямим.
Дві площини, що перетинаються, називаються перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину цих площин, перетинає їх по перпендикулярним прямим.


