
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дві взаємно перпендикулярні площиниСодержание книги Поиск на нашем сайте
Умова завдання. Через дану пряму EF провести площину, перпендикулярну до заданої площини ABC. Побудувати лінію перетину цих площин. Мета завдання: засвоїти методи розв'язування задач на перпендикулярність і взаємний перетин прямої та площини й двох площин. Рекомендації до виконання завдання. Приклад виконання завдання показано на рис. 13. Наведемо деякі теоретичні положення. Пряма m перпендикулярна до площини θ, якщо вона перпендикулярна до двох будь-яких пересічних прямих цієї площини. Для зручності розв'язування задач за пересічні прямі краще взяти горизонталь h і фронталь f площини, тому що прямий кут між m та h і між m та f проектується відповідно на площини П1 та П2 без спотворення. Умова перпендикулярності між прямою m і площиною θ може бути записана так: m┴θ, якщо m1┴h1, m2┴h2. Отже, для побудови площини, перпендикулярної до заданої площини і такої, що проходить через задану пряму, досить із будь-якої точки цієї прямої опустити перпендикуляр на задану площину. Для побудови лінії перетину двох площин необхідно визначити точки перетину двох прямих побудованої площини із заданою та їх з'єднати. Щоб визначити точку перетину прямої з площиною, доцільно застосувати метод допоміжних січних площин. Алгоритм розв'язання задач складається з таких операцій: 1) через задану пряму проводять допоміжну площину Σ; 2) знаходять лінію перетину заданої площини 6 із допоміжною Σ; 3) визначають точку перетину двох прямих – заданої та лінії перетину. Послідовність виконання завдання така: 1. За заданими координатами точок (табл. 11) накреслити проекції трикутника ABC (θ) і прямої EF. 2. Провести у площині трикутника ABC горизонталь h та фронталь f. 3. З точки Е провести перпендикуляр m до площини трикутника. Площина, утворена пряними EF і m, буде перпендикулярна до площини трикутника ABC. 4. Визначити точки М та N перетину прямих EF і m із площиною ABC та з'єднати їх прямою. 5. Видимість площин визначити за допомогою конкуруючих точок. Задача може бути розв'язана за допомогою методів перетворення комплексного рисунка, тобто якщо перетворити задану площину загального положення в площину окремого положення. Для цього можна застосувати методи заміни площин проекцій, плоскопаралельне переміщення та косокутне допоміжне проектування. На прикладі до цього завдання (права частина рис. 13) використано метод заміни площин проекцій. Послідовність виконання завдання така. У площині трикутника ABC потрібно провести горизонталь h, а перпендикулярно до горизонтальної проекції горизонталі – вертикальну площину (її горизонтальний слід – Х14). При цьому горизонталь спроектується в точку h4 (A 4 ≡ 14), а весь трикутник ABC – у пряму А4В4С4. Спроектувавши площину ABC у пряму й опустивши на неї перпендикуляр із точки Е, легко графічно визначити лінію перетину перпендикулярної площини (EF і m) та заданої ABC.
Таблиця 11
Завдання 10
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 147; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

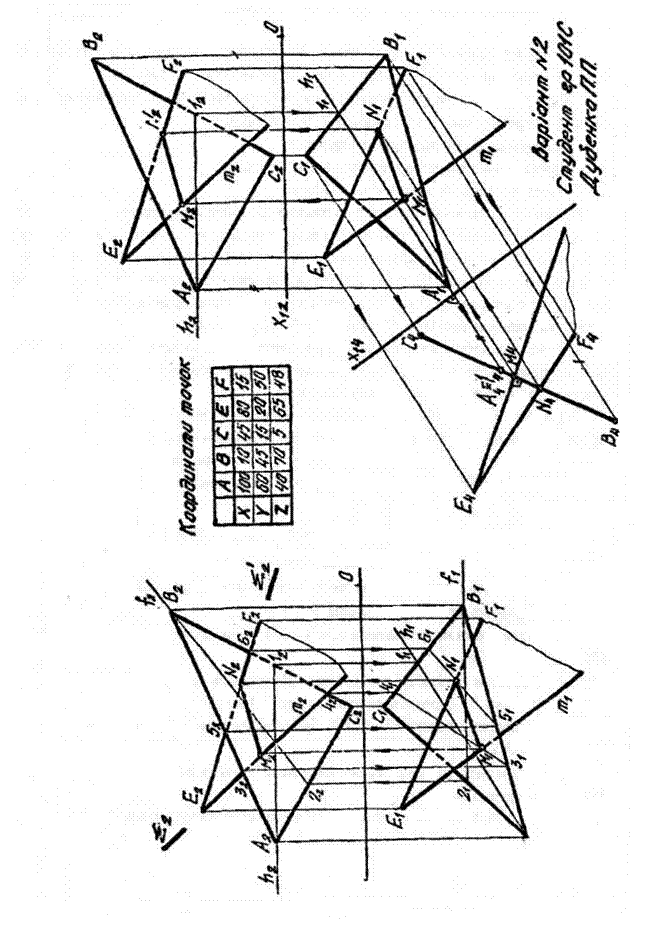

 Рис. 13
Рис. 13


