
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Координати і вектори у просторіСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Координати і вектори у просторі Вектори у просторі. Дії над векторами. Розкладання вектора на складові
називаються співнапрямленими.
Сума двох векторів
Закони додавання векторів · Переставний закон: · Сполучний закон:
Правило паралелограма (на площині) Правило паралелепіпеда (у просторі)
Віднімання векторів
Множення вектора на число Множення вектора на додатне число
Множення вектора на нуль дає нульовий вектор: Множення вектора на від’ємне число
Розкладання вектора за неколінеарними векторами
Кутом між векторами називається кут, утворений рівними їм векторами, що відкладені від спільного початку.
Скалярним добутком двох векторів називаєтся добуток їх довжин на косинус кута між ними.
Перпендикулярність векторів Два вектори називаються перпендикулярними, якщо вони лежать на перепендикулярних прямих. Два вектори перпендикулярні тоді, і тільки тоді, коли скалярний добуток дорівнює нулю. Скалярний квадрат вектора дорівнює квадрату його довжини.
Прямокутна система координат у просторі. Прямі і площини у просторі Аксіоми стереометрії і найпростіші наслідки з них 2.1.1 Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать цій площині.
2.1.2 Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що
2.1.3 Якщо дві різні прямі мають спільну точку, то через них можна провести площину і до того ж тільки одну.
Наслідки з аксіом 2.1.4 Через пряму і точку, яка не лежить на ній, можна провести площину і до того ж тільки одну.
2.1.5
2.1.6 Через три точки, які не лежать на одній прямій, можна провести площину і до того ж тільки одну.
Властивості паралельних площин 2.2.9
2.2.10 Через точку поза даною площиною можна провести площину, паралельну даній, і до того ж тільки одну.
2.2.11 Якщо дві паралельні площини перетинаються третьою, то прямі перетину паралельні.
2.2.12
Проектування трикутників
При проектуванні будь-якого трикутника (гострого, тупокутного, прямокутного, рівнобедреного або рівностороннього) утворюється трикутник довільної форми (гострокутний чи тупокутний).
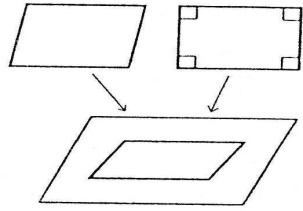
Проектування паралелограмів
Оскільки паралельність відрізків при проектуванні зберігається, паралелограми (а також прямокутники та квадрати) зображуються паралелограмами довільної форми.
При проектуванні ромба незмінною стає одна з діагоналей,
Проектування трапеції
При проектуванні будь-яка трапеція (довільна, рівнобічна, прямокутна) зображується як довільна трапеція.
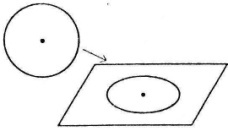
Проектування кола Коло при проектуванні на площину зображується як еліпс.
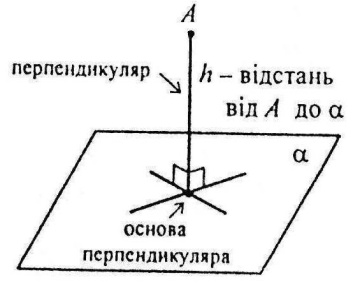
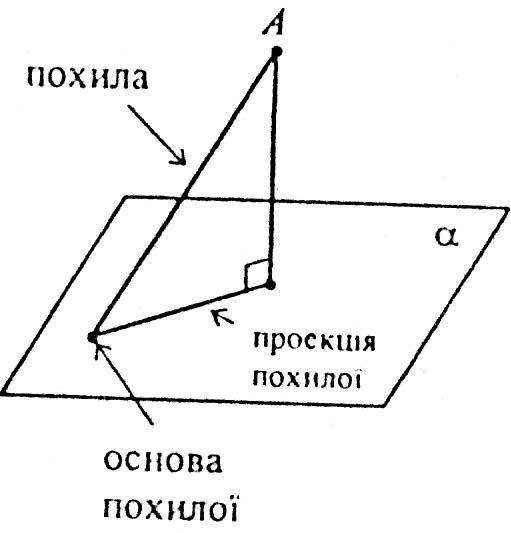
Перпендикуляр і похила
Перпендикуляром, опущеним з даної точки на дану площину, називається відрізок, що сполучає дану точку з точкою площини (основою перпендикуляра) і лежить на прямій, перпендикулярній до площини; при цьому довжина перпендикуляра називається відстанню від даної точки до даної площини.
Похилою, проведеної з даної точки до даної площини, називається будь-який відрізок, який сполучає дану точку з точкою площини (основою похилої) і не є перпендикуляром до площини; відрізок, який сполучає основу перпендикуляра і похилої, проведених з однієї точки, називається проекцією похилої.
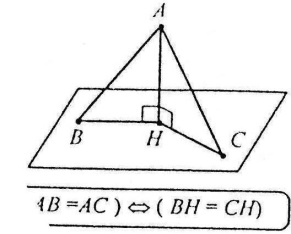
Рівні перпендикуляри, проведені з однієї точки поза площиною до цієї площини, мають рівні проекції. Якщо дві похилі, проведені з однієї точки поза площиною до цієї площини, мають рівні проекції, то вони рівні.
Найбільша з двох похилих, проведених з однієї точки поза площиною до цієї площини, що має більшу проекцію, більша.
Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до її похилої. І навпаки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.
Перпендикулярність площин
Домашнє завдання 2.1 Бічні сторони трапеції паралельні площині 2.2 Пряма а) не лежить у площині б) лежить у площині 2.3 Трикутник 2.4 Точка 2.5 2.6 На рисунку зображено куб а) площини б) площини 2.7
2.8 Дано паралельні прямі 2.9 Діагоналі паралелограма паралельні площині 2.10 Точка M лежить поза площиною трикутника ABC. Яке взаємне розташування прямих BC і MA? 2.11 Прямі 2.12 Дано мимобіжні прямі 2.13 Дано паралелограм 2.14 Дано трикутник АВС. Площина паралельна прямій АС, перетинає сторону АВ у точці Е, а сторону ВС – у точці F. Яка довжина відрізка АС, якщо точка Е – середина АВ, точка F – середина ВС і EF = 12 см?
2.15 Основа 2.16
2.17 2.18 Точка 2.19 Точка
2.20 Пряма
2.21 З точки 2.22 Точка 2.23 Точка А знаходиться на відстані 8см від площини 2.24 З точки А до площини 2.25 Точка А знаходиться на відстані 10см від площини 2.26 З точки 2.27
2.28 2.29 2.30 З точки А до площини 2.31 З точки 2.32 Через сторону правильного трикутника проведено площину, яка утворює з площиною трикутника кут 30°. Знайдіть кути, які утворюють дві інші сторони трикутника з цією площиною. Призми та їх види
Геометричне тіло – частина простору, обмежена якоюсь поверхнею.
Діагоналлю многогранника називається такий відрізок, що сполучає дві вершини многогранника, який не лежить на грані многогранника і не є ребром.
Призма Призма – це многогранник, який складається з двох плоских многокутників (основ), які лежать у різних площинах і суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих многокутників.
Висотою (Н) призми називається відстань між площинами її основ. Властивості призми Основи призми рівні. Площини основ паралельні. Усі бічні ребра рівні і паралельні. Усі бічні грані – паралелограми.
Перпендикулярним називається переріз призми площиною, перпендикулярною до бічного ребра призми, яка перетинає всі бічні ребра.
Пряма призма Прямою називається призма, бічні ребра якої перпендикулярні до основ.
Правильною називається пряма призма, основи якої є правильними многокутниками.
Прямокутний паралелепіпед
Прямокутним називається прямий паралелепіпед, основою якого є прямокутник.
Лінійними розмірами (вимірами) прямокутного паралелепіпеда називаються довжини ребер,що виходять з однієї вершини.
Усі грані прямокутного паралелепіпеда – прямокутники.
Квадрат кожної діагоналі дорівнює сумі квадратів лінійних розмірів: d2=a2+b2+c2
Куб – це прямокутний паралелепіпед, у якого всі ребра рівні.
Усі грані куба – рівні квадрати.
Положення вершини піраміди Вершина рівновіддалена від вершин основи тоді і тільки тоді, коли її проекція є центром описаного навкруги многокутника основи кола або усі бічні ребра однаково нахилені до площини основи. Вершина рівновіддалена від сторін основи тоді і тільки тоді, коли її проекція є центром вписаного у многокутник основи кола або усі бічні грані однаково нахилені до площини основи. Правильна піраміда
Віссю правильної піраміди називається пряма, яка містить її висоту. Апофемою правильної піраміди називається висота бічної грані. Основні властивості Основи циліндрів рівні і лежать у паралельних площинах. Твірні циліндра паралельні і рівні. Висота циліндра дорівнює твірній. При обертанні прямокутника навколо його сторони утворюється циліндр. Циліндр і площини
Осьовий переріз циліндра утворюється площиною, яка проходить через його вісь; це прямокутник, одна сторона якого дорівнює висоті циліндра, а інша – діаметру.
Переріз циліндра площиною, паралельною до його осі, є прямокутником, одна із сторін якого дорівнює висоті циліндра.
Переріз циліндра площиною, паралельною до його основи, є кругом, що дорівнює основі.
Конус
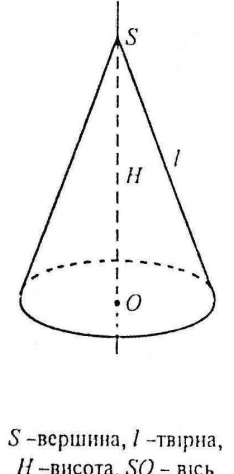
Твірна конуса – це відрізок, що сполучає вершину конуса з точкою на колі основи.
Висота конуса – це перпендикуляр, опущений з його вершини на площину основи (він сполучає вершину з центром основи).
Вісь конуса – це пряма, яка містить його висоту.
Основні властивості Усі твірні конуса рівні між собою. При обертанні прямокутного трикутника навколо його катета утворюється конус. Твірну можна визначити через радіус основи та висоту за теоремою Піфагора: l2=R2+H2 Конус і площини
Осьовий переріз конуса утворюється площиною, яка містить вісь конуса; це рівнобедрений трикутник, бічні сторони якого – твірні конуса, а основа - діаметр основи конуса.
Переріз конуса площиною, яка проходить через його вершину, є рівнобедрений трикутник, у якого бічні сторони є твірними конуса.
Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню – по колу з центром на осі конуса.
Зрізаний конус
Зрізаний конус – це частина конуса, утворена перерізом конуса площиною, паралельною до основи, але не подібна до самого конуса. Основи зрізаного конуса – два круга з різними радіусами. Висота зрізаного конуса – це відстань між площинами його основ. Вісь зрізаного конуса – це пряма, яка проходить через центри його основ. Твірна зрізаного конуса – це частина твірного конуса, яка лежить між основами утвореного зрізаного конуса. Площина, дотична до сфери Куля – це тіло, що складається з усіх точок
Сфера (кульова поверхня) – це межа кулі.
Діаметр – відрізок, який сполучає дві точки (діаметрально протилежні точки кулі) кульової поверхні і проходить через центр кулі.
Перерізи кулі
Будь-який переріз кулі площиною є круг; центр цього круга є основою перпендикуляра, опущеного з центра кулі на січну площину.
Площина, яка проходить через центр кулі, називається діаметральною площиною; вона утворює переріз кулі, який має назву великий круг.
Площина, що має одну спільну точку зі сферою, називається дотичною до сфери Радіус, проведений в точку дотику, перпендикулярний до площини. Домашнє завдання 3.1 У прямокутному паралелепіпеді 3.2 Ребро куба 3.3 Діагональ основи куба дорівнює а. Чому дорівнює діагональ куба? 3.4 Основа прямої призми – трикутник зі стороною с і прилеглими до неї кутами 3.5 Основа прямої призми — трикутник зі стороною 3.6 Основа піраміди – трикутник зі сторонами 13 см, 14 см і 15 см. Знайдіть площу перерізу, який проходить паралельно площині основи і ділить висоту піраміди у відношенні 1:2, рахуючи від вершини піраміди. 3.7 Основа піраміди — трикутник зі стронами 6 см, 25 см і 29 см. Знайдіть площу перерізу, який проходить паралельно площині основи і ділить висоту піраміди у відношенні 1:3, рахуючи від вершини піраміди. 3.8 Висота циліндра дорівнює 6 см, а його об’єм – 18 см 3.9 Кут між твірною 3.10 Кут між твірною 3.11 Висота конуса дорівнює 14 см, а кут при вершині осьового перерізу – 120 3.12 Радіус основи конуса дорівнює 12 см, а кут при вершині осьового перерізу – 120°. Знайдіть твірну конуса. 3.13 Паралельно осі циліндра, радіус основи якого дорівнює 3.14 Висота циліндра дорівнює 8 см, радіус основи – 5 см. На відстані 4 см від осі циліндра паралельно їй проведено площину. Знайдіть площу перерізу, який при цьому утворився. 3.15 У нижній основі циліндра проведено хорду завдовжки 8 см, яка знаходиться на відстані 3 см від центра цієї основи. Знайдіть площу осьового перерізу циліндра, якщо його висота дорівнює 6 см. 3.16 Паралельно осі циліндра, радіус основи якого дорівнює 8 см, проведено площину, що перетинає основу циліндра по хорді, яка стягує дугу, градусна міра якої 120°. Знайдіть площу перерізу, якщо його діагональ дорівнює 16 см. 3.17 Через дві твірні конуса, кут між якими дорівнює 3.18 3.19 У кулі з центром
3.20 У кулі проведено переріз на відстані 5 см від центра кулі. Знайдіть радіус перерізу, якщо радіус кулі дорівнює 13 см. Піраміда
Sповн=Sб+ Sосн Для правильної піраміди
Sб=1/2 Pоснl Площі основи і бічної поверхні правильної піраміди відносяться як косинус кута між бічною гранню та площиною основи: Sосн/Sб=cosj Для зрізаної піраміди Повна поверхня зрізаної піраміди складається з бічної поверхні та двох основ: Sповн= Sб+S1+S2 де S1 і S2 – площі основ. Об’єм призми та піраміди Об’єм призми дорівнює добутку площі основи на висоту H V= SоснH Об’єм призми дорівнює добутку площі перпендикулярного перерізу на довжину бічного ребра l V=Sперпl Об’єм прямокутного паралелепіпеда дорівнює добутку трьох його вимірів V=a b c
|
|
| Поделиться: |

 Відрізок, для якого зазначено, який з його кінців вважають початком, а який – кінцем, називається напрямленим відрізком, або вектором.
Відрізок, для якого зазначено, який з його кінців вважають початком, а який – кінцем, називається напрямленим відрізком, або вектором. Довжиною (модулем) ненульового вектора називається відстань між його початком та кінцем.
Довжиною (модулем) ненульового вектора називається відстань між його початком та кінцем.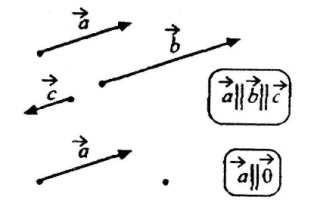 Ненульові вектори називаються колінеарними, якщо вони лежать або на одній прямій, або на паралельних прямих.
Ненульові вектори називаються колінеарними, якщо вони лежать або на одній прямій, або на паралельних прямих. Два однаково напрямлені колінеарних вектори
Два однаково напрямлені колінеарних вектори Вектори називаються рівними, якщо вони співнапрямлені і їх довжини рівні.
Вектори називаються рівними, якщо вони співнапрямлені і їх довжини рівні. Правило трикутника. Сумою двох векторів називається вектор, відкладений від початку першого вектора, кінець якого збігається з кінцем другого вектора.
Правило трикутника. Сумою двох векторів називається вектор, відкладений від початку першого вектора, кінець якого збігається з кінцем другого вектора.



 Різницею двох векторів називається такий вектор, сума якого з другим вектором дорівнює першому.
Різницею двох векторів називається такий вектор, сума якого з другим вектором дорівнює першому. Протилежним даному називається вектор, протилежно напрямлений з даним вектором, який має ту саму довжину.
Протилежним даному називається вектор, протилежно напрямлений з даним вектором, який має ту саму довжину. Віднімання двох векторів рівносильно додаванню до першого вектора, протилежного другому.
Віднімання двох векторів рівносильно додаванню до першого вектора, протилежного другому. Добутком ненульового вектора на число k > 0 називається такий вектор, співнапрямлений даному, довжина якого дорівнює довжині даного вектора, помноженій на k.
Добутком ненульового вектора на число k > 0 називається такий вектор, співнапрямлений даному, довжина якого дорівнює довжині даного вектора, помноженій на k.
 Добутком ненульового вектора на число k < 0 називається такий вектор, протилежно напрямлений даному, довжина якого дорівнює довжині даного вектора, помноженій на k.
Добутком ненульового вектора на число k < 0 називається такий вектор, протилежно напрямлений даному, довжина якого дорівнює довжині даного вектора, помноженій на k. На площині будь-який вектор можна розкласти (записати у вигляді лінійної комбінації) за двома не колінеарними векторами, при цьому коефіцієнти розкладання визначені однозначно.
На площині будь-який вектор можна розкласти (записати у вигляді лінійної комбінації) за двома не колінеарними векторами, при цьому коефіцієнти розкладання визначені однозначно. У просторі будь-який вектор можна розкласти за трьома векторами, що не лежать в одній площині, при цьому коефіцієнти розкладання визначені однозначно.
У просторі будь-який вектор можна розкласти за трьома векторами, що не лежать в одній площині, при цьому коефіцієнти розкладання визначені однозначно. Скалярний добуток векторів
Скалярний добуток векторів
 Косинус кута між векторами дорівнює їх скалярному добутку, поділеному на добуток довжин цих векторів.
Косинус кута між векторами дорівнює їх скалярному добутку, поділеному на добуток довжин цих векторів.

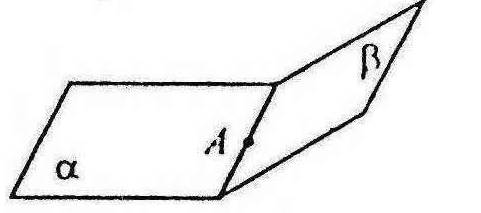 проходить через цю точку.
проходить через цю точку.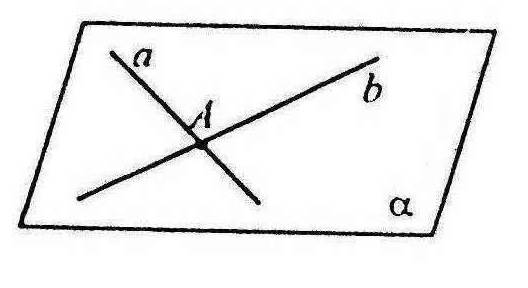

 Якщо дві точки прямої належать площині, то вся пряма належить цій площині.
Якщо дві точки прямої належать площині, то вся пряма належить цій площині.
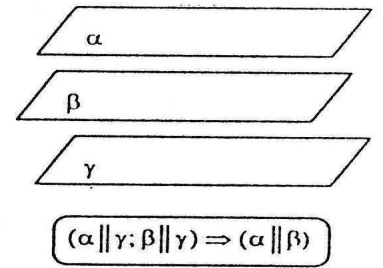 Дві різні площини, які паралельні третій, паралельні.
Дві різні площини, які паралельні третій, паралельні.
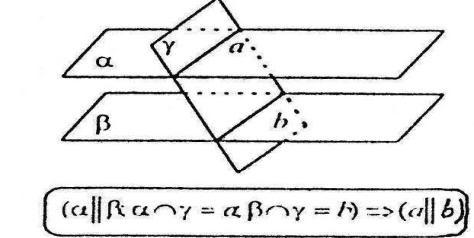
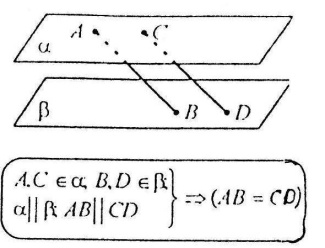 Відрізки паралельних прямих, які містяться між двома паралельними площинами – рівні.
Відрізки паралельних прямих, які містяться між двома паралельними площинами – рівні.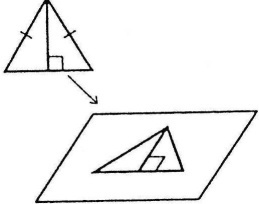

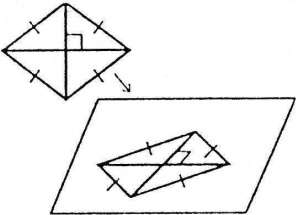 проекцією є паралелограм.
проекцією є паралелограм.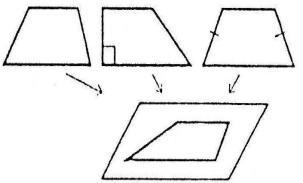
 Властивості перпендикулярів і похилих
Властивості перпендикулярів і похилих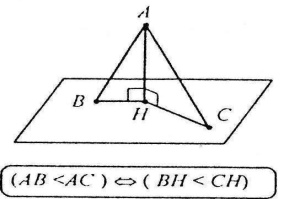
 Теорема про три перпендикуляри
Теорема про три перпендикуляри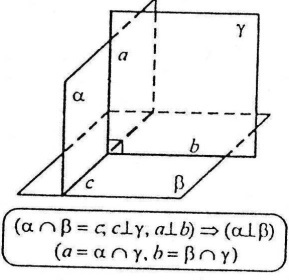 Дві площини, що перетинаються, називаються перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину цих площин, перетинає їх по перпендикулярним прямим.
Дві площини, що перетинаються, називаються перпендикулярними, якщо третя площина, перпендикулярна до прямої перетину цих площин, перетинає їх по перпендикулярним прямим. . Яке взаємне розташування площини
. Яке взаємне розташування площини  і площини трапеції?
і площини трапеції? проходить через середину сторони
проходить через середину сторони  трикутника
трикутника  . Яке взаємне розташування прямих
. Яке взаємне розташування прямих  і
і 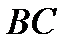 , якщо пряма
, якщо пряма  :
: ;
; і площина
і площина 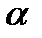 розташовані так, що пряма
розташовані так, що пряма  паралельна площині
паралельна площині  паралельна площині
паралельна площині  і площини
і площини 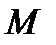 лежить поза площиною трикутника
лежить поза площиною трикутника  . Яке взаємне розташування прямих
. Яке взаємне розташування прямих  і
і 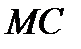 ?
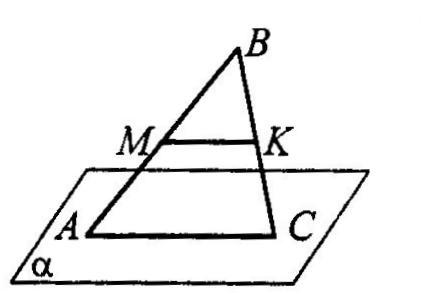
? Дано трикутник ABC. Площина, паралельна прямій AB, перетинає сторону AC у точці M, а сторону BC – у точці K. Яка довжина відрізка MK, якщо точка M – середина AC, точка K – середина BC і AB= 16 см?
Дано трикутник ABC. Площина, паралельна прямій AB, перетинає сторону AC у точці M, а сторону BC – у точці K. Яка довжина відрізка MK, якщо точка M – середина AC, точка K – середина BC і AB= 16 см? . Укажіть пряму перетину
. Укажіть пряму перетину і площини грані
і площини грані 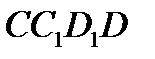 ;
; і площини грані
і площини грані  .
. Сторона
Сторона  трикутника
трикутника  , зображеного на рисунку, належить площині
, зображеного на рисунку, належить площині  , точки
, точки  і
і  – середини сторін
– середини сторін  і
і  трикутника відповідно, точка
трикутника відповідно, точка 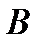 знаходиться поза площиною
знаходиться поза площиною 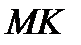 і площини
і площини  і
і  . Скільки існує площин, які проходять через пряму
. Скільки існує площин, які проходять через пряму 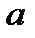 і паралельні прямій
і паралельні прямій  . Яке взаємне розміщення площини
. Яке взаємне розміщення площини  і площини паралелограма?
і площини паралелограма? і
і  паралельні. Як розташована пряма
паралельні. Як розташована пряма  відносно площини
відносно площини  , якщо пряма
, якщо пряма 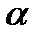 ?
? і
і  і площину
і площину  , прямі
, прямі  і
і  паралельні площині
паралельні площині  і площини
і площини 
 трапеції
трапеції  і
і  – середини бічних сторін трапеції. Яке взаємне розташування прямої
– середини бічних сторін трапеції. Яке взаємне розташування прямої  і площини
і площини 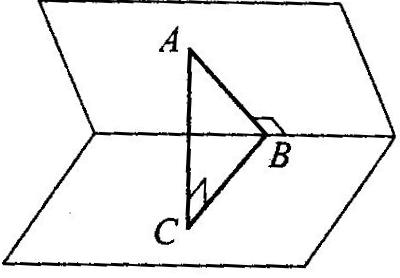 Точка А лежить в одній із граней двогранного кута, зображеного на рисунку. З точки А опущено перпендикуляр АВ на ребро двогранного кута і перпендикуляр АС на другу грань кута, АВ =14 см, АС =7 см. Знайдіть величину двогранного кута.
Точка А лежить в одній із граней двогранного кута, зображеного на рисунку. З точки А опущено перпендикуляр АВ на ребро двогранного кута і перпендикуляр АС на другу грань кута, АВ =14 см, АС =7 см. Знайдіть величину двогранного кута. Пряма
Пряма  перпендикулярна до площини квадрата
перпендикулярна до площини квадрата  , зображеного на рисунку. Укажіть кут між прямою
, зображеного на рисунку. Укажіть кут між прямою  і площиною квадрата.
і площиною квадрата. віддалена від площини
віддалена від площини  на 12 см. З цієї точки проведено до площини
на 12 см. З цієї точки проведено до площини  завдовжки 13 см. Знайдіть довжину проекції похилої
завдовжки 13 см. Знайдіть довжину проекції похилої  . Знайдіть довжину цієї похилої, якщо її проекція на площину
. Знайдіть довжину цієї похилої, якщо її проекція на площину 
 перпендикулярна до площини ромба
перпендикулярна до площини ромба  , зображеного на рисунку. Укажіть кут між прямою
, зображеного на рисунку. Укажіть кут між прямою  і площиною ромба.
і площиною ромба. до площини
до площини 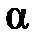 проведено похилі
проведено похилі  і
і  , які утворюють з площиною кути по 30°. Знайдіть відстань від точки
, які утворюють з площиною кути по 30°. Знайдіть відстань від точки 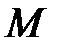 до площини
до площини  , якщо
, якщо  , а довжина відрізка
, а довжина відрізка  дорівнює 10см.
дорівнює 10см.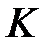 знаходиться на відстані 2см від площини
знаходиться на відстані 2см від площини  . Похилі
. Похилі  і
і  утворюють відповідно з площиною
утворюють відповідно з площиною  кути 60
кути 60  і
і  , а кут між похилими дорівнює
, а кут між похилими дорівнює  . Знайдіть відстань між точками
. Знайдіть відстань між точками  і
і  .
. і
і  проведено похилі АВ і АС, довжини яких 15 см і 20 см відповідно. Знайдіть відстань від точки А до площини
проведено похилі АВ і АС, довжини яких 15 см і 20 см відповідно. Знайдіть відстань від точки А до площини  , якщо проекції похилих на цю площину відносяться як 9:16.
, якщо проекції похилих на цю площину відносяться як 9:16. , а кут між проекціями похилих дорівнює 120°. Знайдіть відстань між точками В і С.
, а кут між проекціями похилих дорівнює 120°. Знайдіть відстань між точками В і С. З точки
З точки  , яка лежить в одній з граней двогранного кута, зображеного на рисунку, опущено перпендикуляр
, яка лежить в одній з граней двогранного кута, зображеного на рисунку, опущено перпендикуляр  на ребро
на ребро  двогранного кута і перпендикуляр
двогранного кута і перпендикуляр  на іншу грань. Знайдіть величину двогранного кута, якщо
на іншу грань. Знайдіть величину двогранного кута, якщо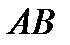 =
=  см,
см, 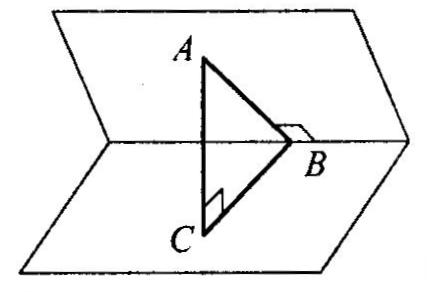 Точка
Точка  лежить в одній із граней двогранного кута, зображеного на рисунку. З точки
лежить в одній із граней двогранного кута, зображеного на рисунку. З точки  опущено перпендикуляр
опущено перпендикуляр  на ребро двогранного кута і перпендикуляр
на ребро двогранного кута і перпендикуляр  на другу грань кута,
на другу грань кута,  = 6
= 6  см,
см,  = 6 см. Знайдіть величину двогранного кута.
= 6 см. Знайдіть величину двогранного кута. З точки
З точки  , яка лежить в одній із граней двогранного кута, зображеного на рисунку, опущено перпендикуляр
, яка лежить в одній із граней двогранного кута, зображеного на рисунку, опущено перпендикуляр  на ребро
на ребро  на іншу грань. Знайдіть величину двогранного кута, якщо
на іншу грань. Знайдіть величину двогранного кута, якщо  см,
см,  см.
см. , а відстань від точки А до площини
, а відстань від точки А до площини  до площини
до площини  і
і  , довжини яких відносяться як 25:26. Знайдіть відстань від точки
, довжини яких відносяться як 25:26. Знайдіть відстань від точки  до площини
до площини  і
і  на цю площину дорівнюють 7 см і 10 см.
на цю площину дорівнюють 7 см і 10 см.
 Многогранник – це таке тіло, поверхня якого складається із скінченної кількості плоских многокутників.
Многогранник – це таке тіло, поверхня якого складається із скінченної кількості плоских многокутників.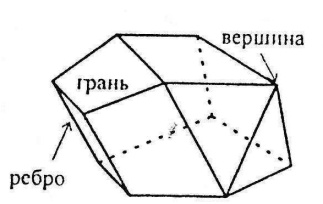 Опуклим називається многогранник, який лежить по один бік від площини кожного з плоских многокутників (граней) на його поверхні; ребра – це сторони граней, вершини – вершини граней.
Опуклим називається многогранник, який лежить по один бік від площини кожного з плоских многокутників (граней) на його поверхні; ребра – це сторони граней, вершини – вершини граней.

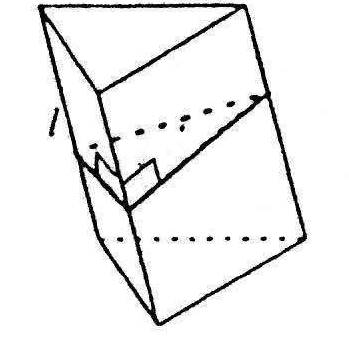 Перпендикулярний переріз призми
Перпендикулярний переріз призми

 Куб
Куб Правильною називається піраміда, основа якої є правильний многокутник, а основа висоти збігається з центром цього многокутника.
Правильною називається піраміда, основа якої є правильний многокутник, а основа висоти збігається з центром цього многокутника.
 Конусом (прямим круговим конусом) називається тіло, яке складається з круга (основи), точки (вершини), яка лежить поза площиною основи на прямій, перпендикулярній до цієї площини, і всіх відрізків, які сполучають вершини конуса з точками основи.
Конусом (прямим круговим конусом) називається тіло, яке складається з круга (основи), точки (вершини), яка лежить поза площиною основи на прямій, перпендикулярній до цієї площини, і всіх відрізків, які сполучають вершини конуса з точками основи.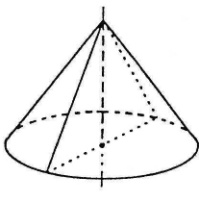



 простору, які знаходяться від даної точки (центра) на відстані, не більше за дану (радіус).
простору, які знаходяться від даної точки (центра) на відстані, не більше за дану (радіус).
 AD = 24 см, CD = 5 см,
AD = 24 см, CD = 5 см,  = 10 см. Чому дорівнює площа прямокутника
= 10 см. Чому дорівнює площа прямокутника  ?
? дорівнює 2 см. Чому дорівнює площа трикутника
дорівнює 2 см. Чому дорівнює площа трикутника  ?
? і
і  . Діагональ бічної грані, що проходить через сторону основи, яка протилежна куту
. Діагональ бічної грані, що проходить через сторону основи, яка протилежна куту  , нахилена до площини основи під кутом
, нахилена до площини основи під кутом  . Знайдіть висоту призми.
. Знайдіть висоту призми. , протилежним цій стороні кутом
, протилежним цій стороні кутом  і прилеглим кутом
і прилеглим кутом 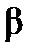 . Діагональ бічної грані, яка містить стонону основи, до якої прилягають кути
. Діагональ бічної грані, яка містить стонону основи, до якої прилягають кути  і
і  , нахилена до площини основи під кутом
, нахилена до площини основи під кутом  . Знайдіть висоту призми.
. Знайдіть висоту призми. . Чому дорівнює площа основи циліндра?
. Чому дорівнює площа основи циліндра? і площиною основи конуса дорівнює
і площиною основи конуса дорівнює  см. Знайдіть висоту конуса.
см. Знайдіть висоту конуса. і площиною основи конуса дорівнює 60
і площиною основи конуса дорівнює 60 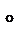 , висота конуса дорівнює
, висота конуса дорівнює  см. Знайдіть твірну конуса.
см. Знайдіть твірну конуса.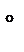 . Знайдіть радіус основи конуса.
. Знайдіть радіус основи конуса. см, проведено площину, що перетинає основу циліндра по хорді, яка стягує дугу, градусна міра якої дорівнює 90°. Знайдіть площу перерізу, якщо кут між діагоналлю перерізу і вказаною хордою дорівнює 60°.
см, проведено площину, що перетинає основу циліндра по хорді, яка стягує дугу, градусна міра якої дорівнює 90°. Знайдіть площу перерізу, якщо кут між діагоналлю перерізу і вказаною хордою дорівнює 60°. , проведено переріз. Знайдіть площу цього перерізу, якщо висота конуса дорівнює h і утворює з його твірною кут
, проведено переріз. Знайдіть площу цього перерізу, якщо висота конуса дорівнює h і утворює з його твірною кут  .
. Через дві твірні конуса, кут між якими дорівнює
Через дві твірні конуса, кут між якими дорівнює  , проведено переріз. Знайдіть площу цього перерізу, якщо радіус основи конуса дорівнює
, проведено переріз. Знайдіть площу цього перерізу, якщо радіус основи конуса дорівнює  , а твірна утворює з площиною основи кут
, а твірна утворює з площиною основи кут  .
. , зображеній на рисунку, проведено переріз з центром
, зображеній на рисунку, проведено переріз з центром  на відстані 12 см від центра кулі. Знайдіть радіус кулі, якщо радіус перерізу дорівнює 9 см.
на відстані 12 см від центра кулі. Знайдіть радіус кулі, якщо радіус перерізу дорівнює 9 см. Повна поверхня піраміди складається з основи та n бічних граней (відповідно до кількості вершин основи)
Повна поверхня піраміди складається з основи та n бічних граней (відповідно до кількості вершин основи) Площа бічної поверхні дорівнює половині добутку периметра основи на довжину апофеми
Площа бічної поверхні дорівнює половині добутку периметра основи на довжину апофеми


