
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Об’єми та площі поверхонь геометричних тілСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Поняття про площу поверхні та об’єм тіла. Площа поверхні многогранника, призми, піраміди
Sповн=Sб+2Sосн де Sосн – площа основи; Sб – площа бічної поверхні (сума площ усіх бічних граней); Sповн – площа повної поверхні.
Sб=Pперп l де l – довжина бічного ребра, Pперп – периметр перпендикулярного перерізу. Площа бічної поверхні прямої призми дорівнює добутку периметру основи на висоту Sб=Pосн Н
Площа бічної поверхні дорівнює добутку периметра основи на висоту Sб=2(а+b)c Площа повної поверхні дорівнює сумі площ шести прямокутників Sповн=2(ab+ac+bc)
Площа повної поверхні куба Sповн=6a2 Піраміда
Sповн=Sб+ Sосн Для правильної піраміди
Sб=1/2 Pоснl Площі основи і бічної поверхні правильної піраміди відносяться як косинус кута між бічною гранню та площиною основи: Sосн/Sб=cosj Для зрізаної піраміди Повна поверхня зрізаної піраміди складається з бічної поверхні та двох основ: Sповн= Sб+S1+S2 де S1 і S2 – площі основ. Для правильної зрізаної піраміди Площа бічної поверхні правильної зрізаної піраміди дорівнює добутку півсуми периметрів її основ на апофему Sб=1/2(P1+P2) l Об’єм призми та піраміди Об’єм призми дорівнює добутку площі основи на висоту H V= SоснH Об’єм призми дорівнює добутку площі перпендикулярного перерізу на довжину бічного ребра l V=Sперпl Об’єм прямокутного паралелепіпеда дорівнює добутку трьох його вимірів V=a b c
Об’єм куба дорівнює третьому степеню (кубу) довжини його ребра V=a3
Об’єм будь-якої піраміди дорівнює третині добутку площі основи на висоту V= 1/3 Sосн H
Площа поверхні циліндра, конуса, кулі
Площа бічної поверхні циліндра дорівнює добутку довжини кола основи на висоту циліндра Sб=2πRH Повна поверхня циліндра складається з бічної поверхні та двох основ Sповн=2πR(H+R)
Sб=πRl Повна поверхня конуса складається з бічної поверхні та основи Sповн=πR(l+R) Площа сфери S=4πR2
Об’єм циліндра, конуса, кулі
Об’єм циліндра дорівнює добутку площі основи на висоту V=πR2H
Об’єм конуса дорівнює третині добутку площі основи на висоту V=1/3 πR2H
Об’єм кулі V=4/3 πR3 Домашнє завдання Частина перша 4.1 Обчисліть площу бічної поверхні прямої призми, основа якої трикутник зі сторонами 20 см, 24 см і 26 см, а бічне ребро дорівнює 6 см. 4.2 Обчисліть площу бічної поверхні прямої призми, основою якої є паралелограм зі сторонами 10 см і 12 см, а бічне ребро дорівнює 10 см. 4.3 Обчисліть площу бічної поверхні прямої призми, основою якої є ромб зі стороною 8 см, а висота призми дорівнює 6 см. 4.4 Обчисліть об’єм призми, основою якої є паралелограм зі сторонами 16 см і 14 см та кутом 45 4.5 Сторона основи правильної трикутної призми дорівнює 14 см, а її бічне ребро 4.6 Обчисліть об’єм правильної чотирикутної призми, сторона основи якої дорівнює 12 см, а висота – 14 см. 4.7 Обчисліть площу бічної поверхні правильної п’ятикутної піраміди, сторона основи якої дорівнює 6 см, а апофема – 10 см. 4.8 Обчисліть площу бічної поверхні правильної восьмикутної піраміди, сторона основи якої дорівнює 18 см, а апофема – 22 см. 4.9 Обчисліть об’єм піраміди, основою якої є прямокутник зі сторонами 26 см і 30 см, а висота піраміди дорівнює 25 см. 4.10 Обчисліть площу бічної поверхні правильної шестикутної піраміди, сторона основи якої дорівнює 4 см, а апофема – 5 см. 4.11 Обчисліть об’єм піраміди, основою якої є ромб з діагоналями 5 см і 9 см, а висота піраміди дорівнює 10 см. 4.12 Обчисліть об’єм піраміди, основою якої є паралелограм зі сторонами 8 см і 10 4.13 Обчисліть площу бічної поверхні циліндра, осьовим перерізом якого є квадрат зі стороною 8 см. 4.14 Чому дорівнює площа бічної поверхні циліндра, діаметр основи якого дорівнює 4 см, а твірна – 9 см? 4.15 Обчисліть площу бічної поверхні циліндра, висота якого дорівнює14 см, а радіус основи – 4 см. 4.16 Обчисліть об’єм циліндра, висота якого дорівнює 6 см, діаметр основи 4см. 4.17 Обчисліть об’єм циліндра, радіус основи якого дорівнює 7 см, а твірна 5 см. 4.18 Чому дорівнює висота циліндра, об’єм якого становить 4.19 Обчисліть площу бічної поверхні конуса, твірна якого дорівнює 8 см, а радіус основи – 10 см. 4.20 Обчисліть площу бічної поверхні конуса, діаметр основи якого дорівнює 12 см, а твірна – 17 см. 4.21 Обчисліть площу бічної поверхні конуса, радіус основи якого дорівнює 3см, а твірна у 3 рази більша за радіус. 4.22 Обчисліть об’єм конуса, висота якого дорівнює 8 см, а радіус основи 9 см. 4.23 Радіуси основ циліндра і конуса рівні, висота циліндра дорівнює 8 см, а конуса – 6 см. Знайдіть відношення об’єму циліндра до об’єму конуса. 4.24 Обчисліть об’єм конуса, висота якого дорівнює 6 см, а радіус основи 5 см. 4.25 Висота конуса дорівнює 9 см, а його об’єм - 6π см3. Чому дорівнює площа основи конуса? 4.26 Чому дорівнює об’єм конуса, радіус основи якого 4.27 Чому дорівнює площа поверхні кулі, радіус якої дорівнює 6 см? 4.28 Чому дорівнює площа поверхні кулі, діаметр якої дорівнює 6см? 4.29 Знайдіть відношення площ поверхонь двох сфер, радіуси яких дорівнюють 5 см і 10 см. 4.30 Обчисліть об’єм кулі з радіусом 6 см. 4.31 Радіус однієї кулі у 2 рази більший за радіус другої кулі. Чому дорівнює об’єм кулі більшого радіуса, якщо об’єм кулі меншого радіуса дорівнює 1 см 4.32 Об'єм першої кулі у 27 разів більший за об’єм другої кулі. Чому дорівнює радіус першої кулі, якщо радіус другої кулі дорівнює 1 см? 4.33 Чому дорівнює радіус кулі, об’єм якої становить 36 Частина друга 4.34 Основа прямої призми – ромб з діагоналями 20см і 48 см. Менша діагональ призми дорівнює 52 см. Обчисліть площу бічної поверхні призми. 4.35 Основа прямої призми – прямокутний трикутник із катетом 12 см і гострим кутом 45°. Об’єм призми дорівнює 216 см3. Знайдіть площу бічної поверхні призми. 4.36 Основа прямої призми – ромб з гострим кутом 30°. Діагональ бічної грані утворює з площиною основи кут 30°. Знайдіть об’єм призми, якщо її висота дорівнює 16 см. 4.37 Основа прямої призми — ромб з гострим кутом 45°. Діагональ бічної грані дорівнює 10 см і утворює з площиною основи кут 60°. Знайдіть об’єм призми. 4.38 Знайдіть об’єм правильної чотирикутної піраміди, сторона основи якої дорівнює 12 см, а діагональний переріз є рівностороннім трикутником. 4.39 Висота правильної чотирикутної піраміди дорівнює 4 см, а апофема 5 см. Обчисліть площу бічної поверхні піраміди. 4.40 Знайдіть об’єм правильного тетраедра, ребро якого дорівнює 8 см. 4.41 Сторона основи правильної трикутної піраміди дорівнює 12 см, а висота піраміди - 2 4.42 Діагональ осьового перерізу циліндра дорівнює 12 см. Знайдіть площу бічної поверхні циліндра, якщо його висота дорівнює діаметру основи. 4.43 У нижній основі циліндра проведено хорду, яку видно з центра нижньої основи під кутом 90°, а з центра верхньої основи – під кутом 60°. Знайдіть площу бічної поверхні циліндра, якщо радіус його основи дорівнює 4 см. 4.44 В основі конуса проведено хорду завдовжки 4.45 Висота конуса дорівнює 20 см, а відстань від центра його основи до твірної 12 см. Знайдіть об’єм конуса. 4.46 Об'єм конуса дорівнює 4.47 Площа повної поверхні конуса дорівнює 200 4.48 Катет прямокутного трикутника дорівнює а, а прилеглий кут дорівнює 4.49 Переріз кулі площиною, яка віддалена від її центра на 15 см, має площу 4.50 Довжина лінії перетину сфери і площини, яка віддалена від її центра на 12 см, дорівнює 4.51 Через кінець радіуса кулі проведено переріз, який утворює з цим радіусом кут 30°. Знайдіть площу поверхні кулі, якщо площа перерізу дорівнює 36
Частина третя 4.52 Основа прямої призми – ромб з більшою діагоналлю d і гострим кутом 4.53 Через сторону нижньої основи і середину протилежного бічного ребра правильної трикутної призми проведено переріз під кутом 45° до площини основи. Знайдіть об’єм призми, якщо площа перерізу дорівнює 4.54 Бічна грань правильної чотирикутної піраміди нахилена до площини основи під кутом 4.55 Основа піраміди – рівнобедрений трикутник з бічною стороною а і кутом 4.56 Апофема правильної чотирикутної піраміди дорівнює 4.57 Хорду нижньої основи циліндра видно із центра цієї основи під кутом 4.58 У нижній основі циліндра проведено хорду, довжина якої дорівнює b. Цю хорду видно із центра нижньої основи під кутом 4.59 У нижній основі циліндра проведено хорду, яку видно із центра цієї основи під кутом 4.60 Через дві твірні конуса, кут між якими дорівнює 1. Погорєлов О.В. Геометрія: Стереометрія: Підручник для 10 – 11 кл. серед.школи.-3-тє видання.-Київ: Освіта, 1997. – 128 с. 2. Збірник завдань для державної підсумкової атестації з математики. 11клас. У 2 книгах. Кн. 1 / М.І.Бурда, О.Я.Біляніна, О.П.Вашуленко та ін. – Харків, „Гімназія”, 2008, – 224 с. 3. Збірник завдань для державної підсумкової атестації з математики. 11клас. У 2 книгах. Кн. 2 / М.І.Бурда, О.Я. Біляніна, О.П.Вашуленко та ін. – Харків, „Гімназія”, 2008, – 224 с.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1085; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.221.252 (0.007 с.) |

 Площа повної поверхні призми дорівнює сумі площі бічної поверхні та площі двох основ:
Площа повної поверхні призми дорівнює сумі площі бічної поверхні та площі двох основ: Площа бічної поверхні призми дорівнює добутку периметру перпендикулярного перерізу на довжину бічного ребра
Площа бічної поверхні призми дорівнює добутку периметру перпендикулярного перерізу на довжину бічного ребра Прямокутний паралелепіпед
Прямокутний паралелепіпед Куб
Куб Повна поверхня піраміди складається з основи та n бічних граней (відповідно до кількості вершин основи)
Повна поверхня піраміди складається з основи та n бічних граней (відповідно до кількості вершин основи) Площа бічної поверхні дорівнює половині добутку периметра основи на довжину апофеми
Площа бічної поверхні дорівнює половині добутку периметра основи на довжину апофеми
 Площа бічної поверхні конуса дорівнює половині добутку довжини кола основи на його твірну
Площа бічної поверхні конуса дорівнює половині добутку довжини кола основи на його твірну
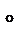 , а висота призми дорівнює
, а висота призми дорівнює  см.
см. см. Обчисліть об’єм призми.
см. Обчисліть об’єм призми. см та кутом 45
см та кутом 45  між ними, а висота піраміди дорівнює 18 см.
між ними, а висота піраміди дорівнює 18 см. см³, а радіус основи дорівнює 2 см?
см³, а радіус основи дорівнює 2 см? , а висота дорівнює радіусу основи?
, а висота дорівнює радіусу основи? ?
? см
см  ?
? см. Знайдіть площу бічної поверхні піраміди.
см. Знайдіть площу бічної поверхні піраміди. см на відстані 4 см від центра основи. Знайдіть об’єм конуса, якщо його твірна нахилена до площини основи під кутом 60°.
см на відстані 4 см від центра основи. Знайдіть об’єм конуса, якщо його твірна нахилена до площини основи під кутом 60°. см
см 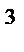 , висота – 12 см. Обчисліть площу бічної поверхні конуса.
, висота – 12 см. Обчисліть площу бічної поверхні конуса. см
см  , а його твірна – 17 см. Знайдіть об’єм конуса.
, а його твірна – 17 см. Знайдіть об’єм конуса. . Знайдіть площу бічної поверхні конуса, утвореного при обертанні цього трикутника навколо даного катета.
. Знайдіть площу бічної поверхні конуса, утвореного при обертанні цього трикутника навколо даного катета. см
см  . Знайдіть площу поверхні кулі.
. Знайдіть площу поверхні кулі. см. Знайдіть площу сфери.
см. Знайдіть площу сфери. см
см  .
. . Через меншу діагональ нижньої основи і вершину гострого кута верхньої основи проведено переріз, який утворює з площиною основи кут
. Через меншу діагональ нижньої основи і вершину гострого кута верхньої основи проведено переріз, який утворює з площиною основи кут  . Знайдіть об’єм призми.
. Знайдіть об’єм призми. см
см  .
. . Відрізок, який сполучає середину висоти піраміди і середину апофеми, дорівнює а. Знайдіть об’єм піраміди.
. Відрізок, який сполучає середину висоти піраміди і середину апофеми, дорівнює а. Знайдіть об’єм піраміди. при основі. Бічна грань піраміди, що містить основу цього трикутника, перпендикулярна до площини основи, а дві інші нахилені до неї під кутом
при основі. Бічна грань піраміди, що містить основу цього трикутника, перпендикулярна до площини основи, а дві інші нахилені до неї під кутом  . Знайдіть об’єм піраміди.
. Знайдіть об’єм піраміди. . Бічне ребро піраміди утворює з площиною основи кут
. Бічне ребро піраміди утворює з площиною основи кут  . Знайдіть об’єм піраміди.
. Знайдіть об’єм піраміди. . Відрізок, що сполучає центр верхньої основи із серединою даної хорди, нахилений до площини основи під кутом
. Відрізок, що сполучає центр верхньої основи із серединою даної хорди, нахилений до площини основи під кутом  . Знайдіть площу бічної поверхні циліндра, якщо радіус основи дорівнює R.
. Знайдіть площу бічної поверхні циліндра, якщо радіус основи дорівнює R. , а відрізок, який сполучає центр верхньої основи із серединою проведеної хорди, утворює з площиною основи кут
, а відрізок, який сполучає центр верхньої основи із серединою проведеної хорди, утворює з площиною основи кут  . Знайдіть об’єм циліндра.
. Знайдіть об’єм циліндра. . Відрізок, що сполучає центр верхньої основи із серединою цієї хорди, дорівнює l і утворює з площиною основи кут
. Відрізок, що сполучає центр верхньої основи із серединою цієї хорди, дорівнює l і утворює з площиною основи кут  . Знайдіть площу бічної поверхні циліндра.
. Знайдіть площу бічної поверхні циліндра. , проведено переріз, який утворює з площиною основи конуса кут
, проведено переріз, який утворює з площиною основи конуса кут  . Знайдіть площу бічної поверхні конуса, якщо його висота дорівнює Н.
. Знайдіть площу бічної поверхні конуса, якщо його висота дорівнює Н. 


