
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Представлення ознак і міри близькості у векторному просторіСодержание книги
Поиск на нашем сайте
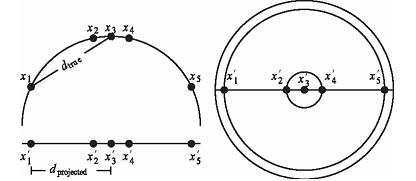
Будемо представляти ознаки у вигляді векторів із простору R|V|. Для того щоб проілюструвати властивості векторів ознак у задачах векторної класифікації, представимо їх у виді точок на площині. Вектори ознак є нормалізованими по довжині одиничними векторами, координати яких лежать на поверхні гіперсфери. Ми можемо розглядати двовимірні площини як проекції поверхні гіперсфери на площину. Відстані між точками на поверхні сфери і між точками на її проекції приблизно збігаються, якщо області на поверхні малі, а проекція обрана корректно. Рішення векторних класифікаторів засновані на понятті відстані, наприклад на обчисленні найближчих сусідів у методі kNN. У цій главі як основна міра близькості обрана евклідова відстань. Між косинусною мірою подібності і відстанню для векторів, нормалізованих по довжині, існує пряма залежність. У векторній класифікації дуже рідко має значення, як виражається близькість двох ознак — через міру подібності чи відстань. Однак, крім ознак, у теорії векторної класифікації велику роль грають центроїди, чи усереднені вектори. Центроїди не є нормалізованими за довжиною. Для таких векторів скалярний добуток, косинусна міра подібності й евклідова відстань, у принципі, поводяться по-різному. Косинусна міра подібності дорівнює
де У такому випадку
В основному при визначенні подібності між ознаками і центроїдом нас будуть цікавити невеликі області, причому чим менше область, тим більше схожими стають властивості всіх трьох мір близькості.
Рис. 3.2. Проекції
Метод Роккіо На рис. 3.1 показано три класи на двовимірній площині: China, UK і Kenya. Ознаки відзначені кружечками, ромбиками і хрестиками. Поділяючі границі (decision boundaries) на малюнку обрані таким чином, щоб розділити три класи, але в іншому їхні властивості довільні. Для класифікації нової ознаки, відзначеної на рисунку зірочкою, ми визначаємо область, у яку вона потрапила, а потім клас, що відповідає цій області (у даному випадку це клас China). Векторна класифікація зводиться до розробки алгоритму, що обчислює “гарні” межі, де термін “гарні” означає високу точність класифікації на даних, не використаних у ході навчання. Для векторної класифікації ознак необхідно визначити межі між класами, оскільки саме вони визначають результат класифікації. Ймовірно, найбільш відомим методом визначення цих меж є метод Роккіо (Rocchio classification), у якому для ідентифікації меж використовуються центроїди. Центроїд класу обчислюється як усереднений вектор чи центр мас членів класу
Тут
Межа між двома класами в методі Роккіо являє собою множину точок, рівновіддалених від двох центроїдів. Наприклад, |a1| = |a2|, |b1| = |b2| і |с1| = |с2|. Ця множина точок завжди утворює лінію. Узагальненням цієї лінії в M- вимірному просторі є гіперплощина, що являє собою множину точок x_, що задовольняють умові w1x1 + w2x2 = b) і двовимірні площини (будь-яка площина в тривимірному просторі визначається рівнянням w1x1 + w2x2 + w3x3 = b).
Рис. 3.3. Класифікація Роккіо
Лінія розділяє площину на дві напівплощини, площина розділяє тривимірний простір на два підпростори і т.д. Таким чином, межами областей класів у методі Роккіо є гіперплощини. Правило класифікації в алгоритмі Роккіо полягає у визначенні області, у яку потрапляє точка. Це еквівалентно пошуку центроїда Алгоритм навчання TrainRocchio(C,D) 1 for each 2 do 3 4 return (
Алгоритм класифікації ApplyRocchio(C,D) 1 return Приклад 3.1. У табл. 3.1. приведено векторні представлення з вагами tf–idf п'яти ознак, отриманих за допомогою формули
Центроїдами класів є два вектори:
(аналогічно
Таблиця 3.1
Критерієм класифікації є евклидова відстань. Як альтернативу можна використовувати косинусну міру подібності.
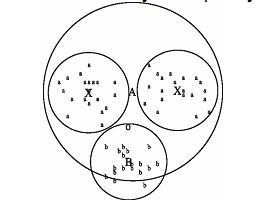
Як зазначено в розділі 3.1, два критерії класифікації іноді приводять до різних результатів. Тут ми навели варіант алгоритму Роккіо, заснований на використанні евклідової відстані, оскільки вона підкреслює тісний зв'язок з методом кластеризації K-середніх (K-means clustering), що буде описаний пізніше. Крім відповідності гіпотезі компактності, класи в класифікації Роккіо повинні мати приблизну форму сфер із приблизно однаковими радіусами. На рис. 3.3 чорний квадрат безпосередньо під межею між класами UK і Kenya більше підходить для класу UK, оскільки клас UK має більш широкий розкид, ніж клас Kenya. Однак алгоритм Роккіо відносить його до класу Kenya, тому що при класифікації він ігнорує особливості розподілу точок у класі і використовує лише відстані до центроїду. Рис. 3.4. Мультимодальний клас “a” складається з двох різних кластерів (невеликі кола у верхній частині малюнка з центрами в точках X). Класифікація Роккіо неправильно віднесе термін “o” до класу термінів “а”, тому що він ближче до центроїду A класу “a”, а не до центроїду B класу “b” Припущення про сферичність на рис. 3.4 також не виконується. Клас “a” неможливо добре описати за допомогою єдиного прототипу, оскільки він складається з двох кластерів. Алгоритм Роккіо часто невірно розпізнає мультимодальні класи такого типу. Прикладом мультимодального класу в задачах текстової класифікації є країни на зразок Бірми, що з 1989 року стала називатися Мьянмою. Два кластери до і після зміни назви не обов'язково розташовані близько один від одного у векторному просторі. Ще одним прикладом, у якому класи рідко являють собою сфери з однаковими радіусами, є задача бінарної класифікації. Більшість бінарних класифікаторів розрізняють клас на зразок China, що займає невелику область у просторі, і його доповнення, розкидане по всьому просторі. Припущення про рівність радіусів привело б до великої кількості хибно-позитивних рішень. Отже, для більшості задач бінарної класифікації необхідно уточнити вирішальне правило
Тут b — позитивна константа. Центроїд “негативних” ознак можна не використовувати взагалі, тому вирішальне правило можна спростити до
Лабораторна робота №4 Метод k найближчих сусідів На відміну від методу Роккіо, метод k найближчих сусідів (k nearest neighbor), чи kNN-класифікація, визначає поділяючі межі локально. У варіанті 1NN кожна ознака відноситься до визначеного класу в залежності від інформації про його найближчого сусіда. У варіанті kNN кожна ознака відноситься до переважного класу найближчих сусідів, де k -параметр методу. В основі методу kNN лежить факт, что відповідно до гіпотези компактності ми очікуємо, что тестова ознака d буде мати таку ж мітку, як і навчальні ознаки в локальній області, що оточує ознаку d. Поділяючі межі в методі 1NN являють собою суміжні сегменти діаграми Вороного (Voronoi tesselation), показаної на рис. 4.1. Діаграма Вороного для множини об'єктів розділяє простір на осередки, що складаються з точок, що ближче до даного об'єкта, ніж до інших. У нашому випадку об'єктами є ознаки. Діаграма Вороного розділяє площину на |D| опуклих багатокутників, кожний з який містить відповідну ознаку (і не містить інших), як показано на рис. 4.1, на якому опуклий багатокутник є опуклою областю двовимірного простору, обмеженою лініями.
Рис. 4.1. Діаграма Вороного і поділяючі межі (подвійні лінії) у методі 1NN. Показано три класи: хрестики, кружечки і ромбики Для довільного параметра kÎ N у методі kNN розглянемо область простору, для якої множина k найближчих сусідів залишається однаковою. Ця область також являє собою опуклий багатокутник, а простір виявляється розділеним на опуклі багатокутники, усередині кожного з якою множина k найближчих сусідів є інваріантною. Метод 1NN не дуже стійкий. Класифікація кожної текстової ознаки залежить від класу, до якого належить окрема навчальна ознака, що може мати невірну мітку чи взагалі бути нетиповим. Метод kNN при k > 1 є більш стійким. Він приписує ознаки до переважаючого класу по k найближчих сусідах, випадковим образом розриваючи зв'язку між ними. Існує імовірнісний варіант методу kNN. Можна оцінити імовірність того, що ознака належить класу c, як частку k найближчих сусідів у класі c. На рис. 4.1 наведений приклад класифікації при k = 3. Оцінки імовірностей того, що ознака, відзначена зірочкою, належить трьом класам, такі: P(клас кружечків|зірочка) = 1/3, P(клас хрестиків|зірочка) = 2/3, P(клас ромбиків|зірочка) = 0. Оцінки методу 3NN (P(клас кружечків|зірочка) = 1/3) і методу 1NN (P(клас кружечків|зірочка) = 1) відрізняються, тому метод 3NN віддає перевагу класу хрестиків, а метод 1NN — класу кружечків. Параметр k у методі kNN часто вибирається на підставі досвіду чи знань про розв'язувану задачу класифікації. Бажано, щоб параметр k був непарним, щоб зменшити імовірність «нічиєї». Найчастіше вибираються значення k = 3 і k = 5, але використовуються і великі значення, між 50 і 100. Як альтернативу параметр k можна вибрати так, щоб він гарантував найкращі результати на відкладеній частині навчального множини. Можна також приписати ваги “голосам” k найближчих сусідів, використовуючи їх косинусну міру подібності. У цій схемі ранги класів обчислюються так
Тут Sk — множина k найближчих сусідів ознаки d' і Ic(d') = 1 тоді і тільки тоді, коли ознака d' належить класу c і Ic(d') = 0 — в противному випадку. Ознака приписується до класу з найбільшим рангом. Зважування за допомогою міри подібності часто виявляється більш точним, ніж просте голосування. Наприклад, якщо два класи мають однакову кількість сусідів, то вибирається клас з більш близькими сусідами. Алгоритм kNN Навчання (з попередньою обробкою) і тестування по методу kNN. Величина pj — це оцінка імовірності P(cj|Sk) = P(cj|d), а cj — множина всіх ознак у класі cj) Алгоритм навчання Train-kNN(C, D) 1 D ' Preprocess(D) 2 k Select-k{C, D ' } 3 return D ', k Алгоритм класифікації Apply-kNN(C, D ', k, d) 1 Sk ComputeNearestNeighbors(D ', k, d) 2 for each cj ÎC 3 do pj | Sk Ç cj |/ k 4 return Приклад 4.1. Відстані між тестовою ознакою і чотирма навчальними ознаками рівні
Метод kNN досить сильно відрізняється від інших алгоритмів класифікації. Навчання методу kNN зводиться до простого визначення параметра k і попередній обробці ознак. Фактично, якщо параметр k обраний заздалегідь, а попередня обробка ознак не передбачена, у методі kNN взагалі відсутня фаза навчання. На практиці попередня обробка, наприклад розбивка на лексеми (tokenization), є обов'язковою. Її доцільно провести один раз на етапі навчання, а не повторювати щораз при класифікації нової ознаки. У класифікації по методу kNN не виробляється оцінка жодного параметру, як у методі Роккіо (центроїди) або в наївному байєсівському методі (апріорні й умовні імовірності). У методі kNN всі екземпляри з навчальної множини просто запам'ятовуються, а потім порівнюються з тестовою ознакою. З цієї причини метод kNN також називають навчанням на основі запам'ятовування (memory-based learning) і навчанням на основі запам'ятовування прецедентів (instance-based learning). Для машинного навчання бажано мати якнайбільше навчальних даних. Однак у методі kNN великі навчальні множини приводять до значного зниження ефективності класифікації. Існує подібність між задачею пошуку найближчого сусіда тестової ознаки і задачею пошуку по довільному запиту, метою якого є ознаки, що мають найбільшу схожість із запитом. Фактично ці дві проблеми являють собою різні варіанти задачі про k найближчих сусідів і відрізняються лише відносною щільністю вектора тестової ознаки (сотні ненульових елементів у методі kNN) і розрідженістю вектора запиту (як правило, у задачі пошуку по довільному запиту кількість ненульових елементів менше десяти). Для забезпечення ефективності довільного пошуку використовується інвертований індекс. Інвертований індекс обмежує пошук тільки тими ознаками, що мають хоча б один загальний термін із запитом. Таким чином, у контексті методу kNN інвертований індекс виявиться ефективним, якщо тестова ознака не має загальних термінів з великою кількістю навчальних ознак. Чи це так, залежить від конкретної задачі класифікації. Якщо ознаки довгі, а список стоп-слів не використовується, то економія часу буде незначною. Однак при коротких ознаках і довгому списку стоп-слів інвертований індекс може скоротити середній час тестування в десять і більш разів. Час пошуку при використанні інвертованого індексу залежить від довжини списку словопозицій термінів із запиту. Довжина списків словопозицій сублінійно зростає при збільшенні розміру колекції, оскільки лексикон збільшується відповідно до закону Хіпса (Heaps’ law): якщо імовірність появи одних термінів зростає, то імовірність появи інших повинна убувати.
Література 1. Маннинг К.Д., Рагхаван П., Шютце Х. Введение в информационный поиск.— М.: Изд-во “Вильямс”, 2011. 2. Воронцов К. Машинное обучение (курс лекций). http://www.machinelearning.ru/wiki/index.php?title=Машинное_обучение_(курс_лекций%2C_К.В.Воронцов)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.241.235 (0.009 с.) |

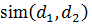 =
= 
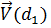 і
і 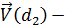 вектори ознак документів d1 і d2,
вектори ознак документів d1 і d2,  - скалярний добуток цих векторів,
- скалярний добуток цих векторів, 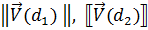 - норми векторів ознак. Позначимо через
- норми векторів ознак. Позначимо через  і
і 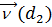 - нормалізовані вектори, тобто
- нормалізовані вектори, тобто  ,
, 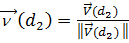 .
. .
.

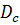 — множина ознак із простору документів D, що належать класу c:
— множина ознак із простору документів D, що належать класу c: },
},  - нормалізований вектор ознаки
- нормалізований вектор ознаки  .
. =b. Тут
=b. Тут 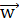 — M- вимірний вектор нормалі (normal vector) до гіперплощини, а b — константа. Це визначення гіперплощин охоплює лінії (будь-яка лінія на двовимірній площині описується рівнянням
— M- вимірний вектор нормалі (normal vector) до гіперплощини, а b — константа. Це визначення гіперплощин охоплює лінії (будь-яка лінія на двовимірній площині описується рівнянням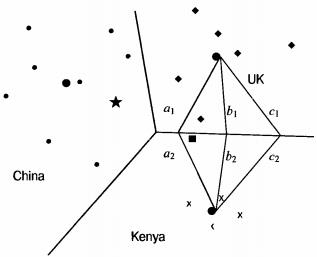
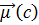 , до якого точка лежить ближче, ніж до інших центроідів, і приписуванню цієї точці до класу c. Як приклад розглянемо зірочку, яка належить області China, тому алгоритм Роккіо відносить її до класу China. Псевдокод алгоритму Роккіо представлений нижче.
, до якого точка лежить ближче, ніж до інших центроідів, і приписуванню цієї точці до класу c. Як приклад розглянемо зірочку, яка належить області China, тому алгоритм Роккіо відносить її до класу China. Псевдокод алгоритму Роккіо представлений нижче.
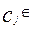 C
C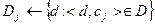
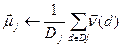
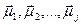 )
)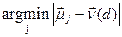
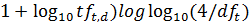 , якщо
, якщо  >0.
>0. (
(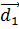 +
+ 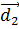 +
+ 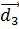 ) і
) і 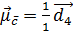 . Відстані тестової ознаки від центроїдів дорівнюють
. Відстані тестової ознаки від центроїдів дорівнюють 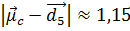 і
і 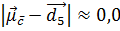 . Отже, алгоритм Роккіо віднесе ознаку
. Отже, алгоритм Роккіо віднесе ознаку 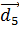 до класу c. Поділяюча гіперплощина в цьому випадку описується наступними параметрами
до класу c. Поділяюча гіперплощина в цьому випадку описується наступними параметрами  ≈(0 0,71 0,71 1/3 1/3 1/3), b=1/3. Обчислення вектора
≈(0 0,71 0,71 1/3 1/3 1/3), b=1/3. Обчислення вектора 
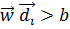 для 2 ≤ i ≤3) і
для 2 ≤ i ≤3) і 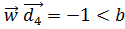 .Таким чином, ознаки з класу c лежать вище напівплощини
.Таким чином, ознаки з класу c лежать вище напівплощини 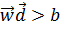 . а ознаки з класу
. а ознаки з класу 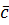 — нижче напівплощини
— нижче напівплощини 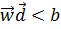 .
.
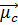
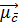
 c=
c= 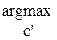 cos(
cos(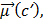
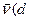 ))
))
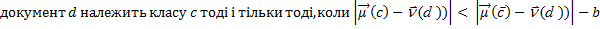
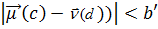 , де b' — позитивна константа.
, де b' — позитивна константа.
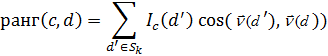
 pj
pj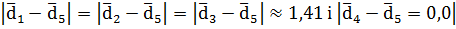 . Отже, найближчим сусідом ознаки d5 є ознака d4, і метод 1NN припише ознаку d5 до класу ознаки d4, тобто до класу
. Отже, найближчим сусідом ознаки d5 є ознака d4, і метод 1NN припише ознаку d5 до класу ознаки d4, тобто до класу 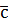 .
.


