Класифікація у векторному просторі. Метод Роккіо.

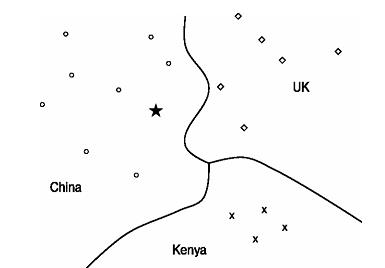
У цій лабораторній роботі для представлення ознак при класифікації текстів ми використаємо векторну модель. У ній кожна ознака розглядається як вектор, що складається з дійсних чисел, як правило — з ваг tf–idf кожного терміна, де вага tf-idf = tf × idf, tf — частота терміну в документі, idf — обернена частота терміну в документі, яка дорівнює , де N — загальна кількість документів у колекції, а df — кількість документів, в яких зустрічається термін. Таким чином, простір ознак X (тобто область визначення функції класифікації γ) збігається з простором R^|V|, де V — кількість термінів у колекції. В основі використання моделі векторного простору для класифікації лежить гіпотеза компактності.

Гіпотеза компактності. Ознаки, що належать одному і тому ж класу, утворюють компактну область, причому області, що відповідають різним класам, не перетинаються.

Існує багато задач класифікації текстів, зокрема задачі, у яких класи відрізняються вживанням слів. Наприклад, ознаки в класі China, швидше за все, мають великі значення на осях, що відповідають термінам Chinese, Beijing і Mao, у той час як ознаки з класу UK — великі значення на осях, що відповідають термінам London, British і Queen. Отже, ознаки з двох класів утворять різні області,що не перетинаються. Між цими областями можна провести межі і класифікувати нові ознаки. Саме це є темою даної лабораторної роботи.

Рис.3.1 Класифікація на три класи.

Чи заповнює множина ознак неперервну область, залежить від конкретного вибору представлення ознаки: типу зважування, списку стоп-слів (слів, що не несуть семантичного навантаження і є займенниками, сполучниками тощо) і т.д. Для того, щоб переконатися, що представлення ознаки відіграє дуже важливу роль, розглянемо два класи (ознак): написані групою авторів і написані окремою людиною. Висока частота займенника першої особи I (я), очевидно, є ознакою другого класу. Однак ця інформація, швидше за все, буде вилучена з представлення ознаки, якщо використовується список стоп-слів. Якщо представлення ознаки обране невдало, то гіпотеза компактності не буде виконуватися і класифікація у векторному просторі стане неможливою. У даному випадку можна повторити ті ж міркування, що привели нас до зважених представлень, зокрема — до нормалізованого по довжині представлення tf–idf. Наприклад, термін, що п'ять разів зустрічається в ознаці, повинен мати більшу вагу, ніж термін, що зустрічається тільки один раз, але приписувати такому терміну в п'ять разів більшу вагу означає приписувати йому занадто велике значення. У векторній моделі класифікації не слід застосовувати незважені і ненормалізовані частоти.

У цій і наступній лабораторній роботах розглядаються дві моделі векторної класифікації: Роккіо (Rocchio) і kNN (k nearest neighours — k найближчих сусідів). Класифікація Роккіо розділяє векторний простір на області, що оточують центроїди, чи прототипи, по одному для кожного класу. Ці центроїди являють собою центри мас всіх ознак у класі. Класифікація Роккіо проста в реалізації й ефективна по швидкості роботи, але неточна, якщо класи далекі від сфер із приблизно однаковими радіусами. Метод kNN, чи класифікація по k найближчих сусідах (k nearest neighbor), описана в наступній лабораторній роботі, відносить тестову ознаку до класу, якому належать k його найближчих сусідів. Метод kNN не вимагає явного навчання і допускає використання навчальної множини в процесі класифікації без попередньої обробки. Він має велику часову складність порівняно з іншими методами класифікації ознак. Якщо навчальна множина велика, то метод kNN краще справляється з несферичними й іншими складними класами, ніж метод Роккіо.

Багато класифікаторів текстів можна розглядати як лінійні класифікатори, тобто класифікатори, засновані на простій лінійній комбінації ознак. Такі класифікатори розбивають простір ознак на області за допомогою поділяючих гіперплощин (decision hyperplanes). Нелінійні моделі мають багато параметрів, які варто підігнати на обмеженому обсязі даних для навчання, і при цьому для невеликих і зашумленних наборів даних зростає імовірність помилок. Застосовуючи бінарні класифікатори для рішення задач з декількома класами, ми інтерпретуємо їх або як задачі однозначної класифікації (one-of), тобто ознака повинна бути віднесена тільки до одного з взаємно виключних класів, або як задачі багатозначної класифікації (any-of), тобто ознака може бути приписана будь-якій кількості класів. Бінарні класифікатори розв’язують задачу багатозначної класифікації, а їх комбінації можна використовувати для розв’язування задач однозначної класифікації.