
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наївна байєсова класифікація текстів.Содержание книги Поиск на нашем сайте
Розглянемо метод навчання з учителем — мультиноміальний наївний метод Байєса (Naive Bayes — NB). У цьому методі імовірність того, що документ d належить класу c, обчислюється в такий спосіб:
Тут Мета класифікації текстів — знайти найкращий клас для документа. У методі NB найкращим вважається клас сmap, що має максимальну апостеріорну імовірність (maximum a posteriori - MAP).
Ми пишемо У рівності (1.2) перемножуються кілька умовних імовірностей, по одній для кожного значення
Рівність (1.3) допускає просту інтерпретацію. Кожен логарифм умовної імовірності Як оцінити імовірності
Тут Оцінимо умовну імовірність
Тут З оцінкою максимальної правдоподібності позв'язана наступна проблема: якщо пара термін-клас не зустрічаються в навчальних даних, то відповідно і оцінка даного терміну для класу дорівнює нулю. Наприклад, якщо термін WTO у навчальних даних зустрічається тільки в документах класу China, то оцінка цього терміну для інших класів, наприклад, класу UK, дорівнюють нулю.
Тепер умовна імовірність класу UK щодо документа Britain is a member of the WTO, що складається з одного речення, дорівнює нулю, оскільки в рівності (4.1) ми перемножуємо умовні імовірності для всіх термінів. Очевидно, что модель повинна привласнювати класу UK високу імовірність, оскільки в пропозиції зустрічається термін Britain. Втім, не можна просто відкинути нульову імовірність для терміна WTO, незалежно від того наскільки багато є свідчень на користь класу UK, забезпечених іншими ознаками. Ця оцінка дорівнює нулю через рідкість терміна. Навчальні дані ніколи не бувають великими настільки, щоб частота рідких термінів оцінювалася адекватно, як, наприклад, частота терміна WTO у документах класу UK. Для того щоб позбутися від нуля, ми використовуємо згладжування Лапласа (Laplace smoothing), просто додаючи одиницю до кожної частоти.
Тут
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.192.173 (0.009 с.) |

 . (1.1)
. (1.1) - умовна імовірність того, що термін
- умовна імовірність того, що термін  з'явиться в документі з класу c,
з'явиться в документі з класу c,  , P(c) — апріорна імовірність того, що документ належить класу c. Якщо терміни документа не дозволяють чітко відокремити один клас від іншого, то варто вибрати той з них, що має більш високу апріорну імовірність. Послідовність
, P(c) — апріорна імовірність того, що документ належить класу c. Якщо терміни документа не дозволяють чітко відокремити один клас від іншого, то варто вибрати той з них, що має більш високу апріорну імовірність. Послідовність  складається з лексем документа d, які входять в словник документу, що використовується для класифікації, а
складається з лексем документа d, які входять в словник документу, що використовується для класифікації, а  — кількість таких лексем у документі d. Наприклад, послідовність
— кількість таких лексем у документі d. Наприклад, послідовність  (1.2)
(1.2) , а не P, тому що не знаємо справжніх параметрів P(c) і
, а не P, тому що не знаємо справжніх параметрів P(c) і  , а можемо лише оцінити їх за допомогою навчальних множин.
, а можемо лише оцінити їх за допомогою навчальних множин. . Це може призвести до переповнення машинної пам'яті і втрати значущих розрядів. Отже, краще замінити добуток імовірностей додаванням їх логарифмів. Клас з найбільшим значенням логарифма імовірності залишається найбільш ймовірним, тому що log(xy) = log(x) + log(y) і логарифмічна функція монотонна. Отже, у наївному методі Байєса насправді потрібно знайти точку максимуму наступної функції
. Це може призвести до переповнення машинної пам'яті і втрати значущих розрядів. Отже, краще замінити добуток імовірностей додаванням їх логарифмів. Клас з найбільшим значенням логарифма імовірності залишається найбільш ймовірним, тому що log(xy) = log(x) + log(y) і логарифмічна функція монотонна. Отже, у наївному методі Байєса насправді потрібно знайти точку максимуму наступної функції
 |c) — це вага, що вказує, наскільки важливий термін tk для класу c. Аналогічно, апріорна імовірність
|c) — це вага, що вказує, наскільки важливий термін tk для класу c. Аналогічно, апріорна імовірність  — це вага, що характеризує відносну частоту класу c. Ті класи, що зустрічаються більш часто, частіше є правильними, ніж рідкісні. Таким чином, клас, сума логарифмів імовірностей і ваг термінів для якого має максимальне значення є аргументом на користь того, що документ належить цьому класу
— це вага, що характеризує відносну частоту класу c. Ті класи, що зустрічаються більш часто, частіше є правильними, ніж рідкісні. Таким чином, клас, сума логарифмів імовірностей і ваг термінів для якого має максимальне значення є аргументом на користь того, що документ належить цьому класу і
і  |c)? Спочатку спробуємо одержати оцінку максимальної правдоподібності, яка є відносною частотою і відповідає найбільш вірогідній величині кожного параметру при заданих навчальних даних. Для апріорних імовірностей оцінка має наступний вигляд
|c)? Спочатку спробуємо одержати оцінку максимальної правдоподібності, яка є відносною частотою і відповідає найбільш вірогідній величині кожного параметру при заданих навчальних даних. Для апріорних імовірностей оцінка має наступний вигляд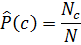
 — кількість документів у класі c, а
— кількість документів у класі c, а  — загальна кількість документів в колекції.
— загальна кількість документів в колекції. ,
, — кількість появ терміна t у навчальних документах із класу c з урахуванням багаторазових появ терміна в документі. Ця оцінка заснована на припущенні про позиційну незалежність: умовні імовірності появи терміну однакові незалежно від позиції цього терміну в документі і враховують тільки кількість появ терміну в документі.
— кількість появ терміна t у навчальних документах із класу c з урахуванням багаторазових появ терміна в документі. Ця оцінка заснована на припущенні про позиційну незалежність: умовні імовірності появи терміну однакові незалежно від позиції цього терміну в документі і враховують тільки кількість появ терміну в документі. |UK)=0.
|UK)=0.
 = |V| — кількість термінів у словнику. Згладжування Лапласа можна інтерпретувати як апріорний рівномірний розподіл (кожен термін зустрічається в кожнім класі по одному разі), що потім уточнюється на основі навчальних даних, що надходять.
= |V| — кількість термінів у словнику. Згладжування Лапласа можна інтерпретувати як апріорний рівномірний розподіл (кожен термін зустрічається в кожнім класі по одному разі), що потім уточнюється на основі навчальних даних, що надходять.


