Ортогональні проекції прямої

ЗБІРКА ЗАДАЧ

з нарисної геометрії

для самостійної роботи студентів

напряму підготовки «Гірництво»

усіх форм навчання

Кривий Ріг – 2011

Укладачі: В.А. Дворніков, к.т.н., доцент,

В.С. Кравець, к.т.н., доцент,

О.П. Буршенко, викладач.

Відповідальний за випуск: В.А. Дворніков, к.т.н., доцент.

Рецензент: А.Н. Пижик, к.т.н., доцент.

У запропонованому збірнику наведено основні теоретичні положення та задачі з кожного розділу нарисної геометрії, розв’язання яких значно покращить якість самостійної роботи студентів. Збірник задач рекомендується для студентів професійного спрямування «Гірництво» усіх форм навчання

Розглянуто Схвалено

на засіданні кафедри вченою радою

нарисної геометрії та механіко-машинобудівного

інженерної графіки факультету

Протокол № __ Протокол № __

від «__» ________2011 від «__» ________2011

ЗМІСТ

ВСТУП.. 4

1 Ортогональні проекції точки. 6

2 Ортогональні проекції прямої 7

3 Взаємне положення двох прямих. 11

4 Комплексне креслення площини. 13

5 Взаємне положення прямої та площини, двох площин. 16

6 Перетин двох площин, прямої та площини. 21

7 Перетворення ортогонального креслення. 23

8 Геометричні поверхні 28

9 Перетин поверхонь площиною та прямою.. 30

10 Взаємний перетин поверхонь. Розгортки. 32

11 Зображення: види, розрізи, перерізи, виносні елементи (ГОСТ 2.305-68) 36

12 Аксонометричні проекції 39

13 Проекції з числовими позначками. Пряма. Дві прямі 41

14 Проекції з числовими позначками. Площина. Взаємне положення двох площин, прямої та площини. 43

15 Топографічні поверхні 46

ЛІТЕРАТУРА.. 48

ВСТУП

Теоретичною основою інженерної графіки є нарисна геометрія, яка розглядає рішення математичних та інженерно-технічних задач за допомогою графічних методів. При цьому використовується метод проекціювання, який дозволяє отримати графічні зображення геометричних образів на три взаємно перпендикулярні площини проекцій П₁, П₂ і П₃.

Найбільш поширеним є ортогональне, або прямокутне проекціювання. При такому проекцію ванні з будь-якої точки геометричного образу, який знаходиться у просторі, проводять перпендикуляри до перетину з П₁, П₂ та П₃.

Таким чином отримують проекції різних точок, прямих, площин та інших геометричних елементів.

На основі аналізу проекцій, використання відповідних теоретичних положень та методик графічних побудов на кресленні отримують рішення вищезгаданих задач.

Для рішення кожної задачі необхідно:

1) вивчити відповідний теоретичний розділ курсу;

2) проаналізувати графічну умову задачі (визначити положення відносно П₁, П₂, П₃ та основні властивості проекцій кожного геометричного образу);

3) розробити план рішення задачі, виходячи з умови мінімальної кількості графічних побудов;

4) записати алгоритм рішення (послідовність операцій) задачі;

5) виконати необхідні побудови.

При написанні алгоритму слід використовувати наступні позначення та символи:

1) площини проекцій – горизонтальна П₁, фронтальна П₂, профільна П₃;

2) вісі проекцій – х, у, z;

3) позначення проекцій точок – горизонтальна А₁, фронтальна А₂, профільна А₃;

4) проекції точки А на вісі проекцій – A_x, A_y, A_z;

5) проекції відрізка прямої – А₁В₁, А₂В₂, А₃В₃;

6) h – горизонталь, f – фронталь, p – профільна пряма (прямі рівня);

7) прямі – a, b, c, d,…;

8) площини – А (альфа), Г (гамма), Δ (дельта), Σ (сигма), Θ (тета);

9) сліди площин – горизонтальний Г_П1, фронтальний - Г_П2, профільний - Г_П3;

10) належність - Ì, Î;

11) паралельність - ||;

12) перпендикулярність - ^;

13) дотичність –

14) мимобіжність –

15) співпадання - ≡;

16) пересічність - ∩, Х;

17) рівність, результат - =;

18) перетворення - ®;

19) еквівалентність – Û;

20) знак імплікації: якщо …, то … - Þ.

Ортогональні проекції точки

Механізм утворення проекції точки пояснює об’ємна модель (рис. 1). Для отримання проекцій точки А необхідно побудувати перпендикуляри до перетину з П₁, П₂, П₃.

Точки перетину перпендикулярів з П₁, П₂, П₃ визначають положення А₁, А₂, А₃. A_x, A_y, A_z – проекції точки А на вісі X, Y, Z.

На практиці використовують площинне креслення (епюр Монжа), яке отримують при суміщенні П₁ та П₃ з П₂ за напрямком стрілок (рис. 2).

Рис. 1 Рис. 2

Основні властивості площинного креслення Монжа (рис. 2):

1) А₂А₁^Х; 2) А₂А₃^Z; 3) |A₁A_X|=|A_ZA₃|=|AA₂|.

1.1 Побудувати проекції точок за їх координатами:

А(10;20;30); В(15;25;0); С(0;30;35); D(20;0;40);

E(25;0;0); F(0;35;0); K(0;0;0).

1.2 Побудувати проекції точки А` симетрично точці А відносно площини П₁.

1.3 Побудувати проекції L за координатами L(15;-20;30).

1.4 Побудувати відсутні проекції точок

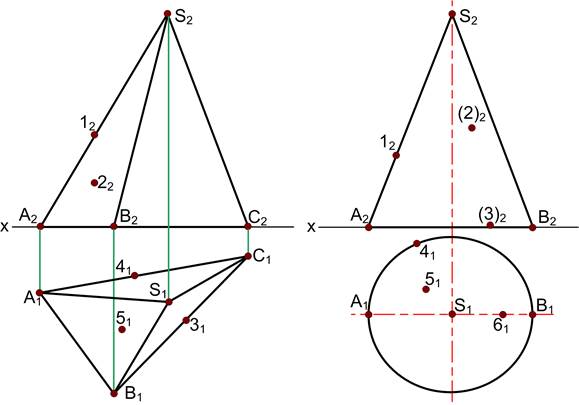
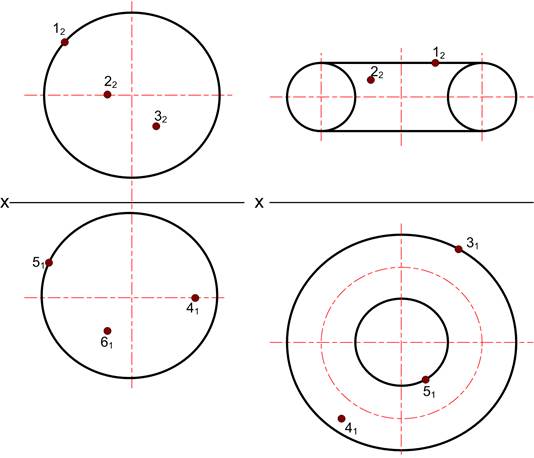
Геометричні поверхні

В нарисній геометрії поверхні розглядають як результат послідовних положень однієї лінії (твірної) при її переміщенні вздовж іншої лінії (направляючої).

Лінія лежить на поверхні, якщо вона проходить через дві, або більше, точок цієї поверхні.

Точка належить поверхні, якщо вона належить лінії, що знаходиться на поверхні.

8.1 Побудувати відсутні проекції точок, які знаходяться на поверхнях.

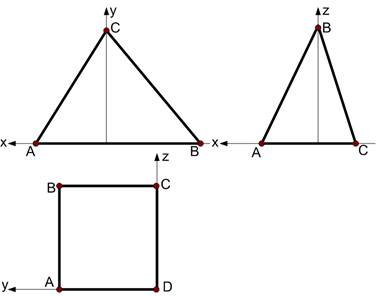
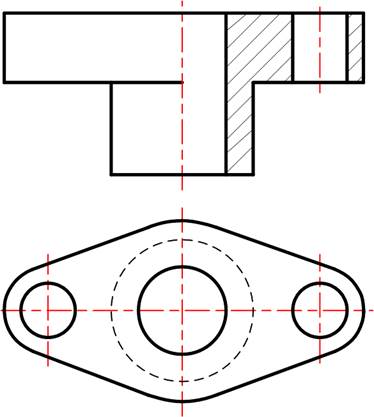
Аксонометричні проекції

Аксонометричні проекції використовують для побудови наочних (об’ємних) зображень геометричних образів та технічних деталей. Аксонометричні зображення будують на основі ортогонального креслення.

Ізометрія. Ізометричні вісі X’, Y’, Z’ розташовані під кутами 120º. Коефіцієнт спотворення лінійних розмірів за осями X’, Y’, Z’: K_x’=K_y’=K_z’.

Диметрія. Відносно лінії горизонту вісь Х’ розташована під кутом 7º10’, вісь Y’ - 41º25’. Коефіцієнт спотворення лінійних розмірів за осями X’, Y’, Z’: K_x’=K_y’=1; K_z’=0,5. тобто всі лінійні розміри за віссю Y’ необхідно зменшувати в два рази.

12.1 Побудувати ізометричну проекцію геометричних фігур.

12.2 Побудувати диметричну проекцію геометричних фігур попередньої задачі.

12.3 На основі ортогонального креслення побудувати ізометрію та диметрію з вирізом четвертої частини по осях X’, Y’.

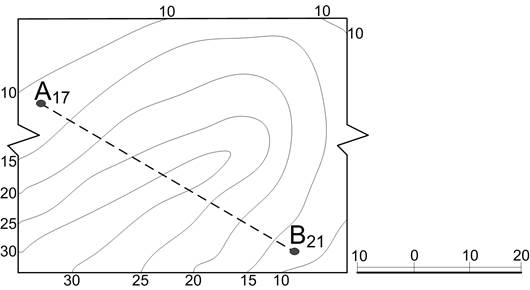
Топографічні поверхні

До топографічних поверхонь відносяться найбільш складні геометричні поверхні неправильних форм, які не мають чітких законів утворення. Найбільш типовим прикладом таких поверхонь є земна поверхня. Для зображення топографічних поверхонь на креслені використовують горизонталі – криві лінії, які з’єднують точки з однаковими числовими позначками.

15.1 Визначити межі земляної споруди та побудувати вертикальний розріз А-А, і_в=1:1, і_н=2:3.

15.2 Визначити точки перетину прямої АВ та топографічної поверхні.

ЛІТЕРАТУРА

1. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометри, М. Физматгиз, 1971, 360 с.

2. Держстандарти ЄСКД. Загальні правила виконання креслень, М., 1983, 215 с.

3. Ломоносов Г.Г. Инженерная графика, М. Недра, 1984, 283 с.

4. Михайленко В.Є., Ванін В.В., Ковальов С.М. Інженерна графіка, Київ «Каравела», «Новий світ-2000», 2002, 332 с.

5. Михайленко В.Є., Євстифеев М.Ф., Ковальов С.М., Кащенко О.В. Нарисна геометрія, К. Вища школа, 1993, 271 с.

6. Михайленко В.Є., Найдиш В.М., Підкоритов А.М., Скидан І.А. Інженерна та комп’ютерна графіка, К., Вища школа, 2001, 352 с.

7. Хаскін А.М. Креслення, К. Вища школа, 1976, 457 с.

Збірка задач з нарисної геометрії для самостійної роботи студентів напряму підготовки «Гірництво» усіх форм навчання

УКЛАДАЧІ: Володимир Андрійович Дворніков

Валентин Сергійович Кравець

Ольга Петрівна Буршенко

Реєстраційний № ___

Підписано до друку _____________2011

Формат А4

Обсяг 49 сторінок

Тираж ___ примірників

Видавничий центр КТУ,

м. Кривий Ріг,

вул. ХХII партз’їзду, 11

ЗБІРКА ЗАДАЧ

з нарисної геометрії

для самостійної роботи студентів

напряму підготовки «Гірництво»

усіх форм навчання

Кривий Ріг – 2011

Укладачі: В.А. Дворніков, к.т.н., доцент,

В.С. Кравець, к.т.н., доцент,

О.П. Буршенко, викладач.

Відповідальний за випуск: В.А. Дворніков, к.т.н., доцент.

Рецензент: А.Н. Пижик, к.т.н., доцент.

У запропонованому збірнику наведено основні теоретичні положення та задачі з кожного розділу нарисної геометрії, розв’язання яких значно покращить якість самостійної роботи студентів. Збірник задач рекомендується для студентів професійного спрямування «Гірництво» усіх форм навчання

Розглянуто Схвалено

на засіданні кафедри вченою радою

нарисної геометрії та механіко-машинобудівного

інженерної графіки факультету

Протокол № __ Протокол № __

від «__» ________2011 від «__» ________2011

ЗМІСТ

ВСТУП.. 4

1 Ортогональні проекції точки. 6

2 Ортогональні проекції прямої 7

3 Взаємне положення двох прямих. 11

4 Комплексне креслення площини. 13

5 Взаємне положення прямої та площини, двох площин. 16

6 Перетин двох площин, прямої та площини. 21

7 Перетворення ортогонального креслення. 23

8 Геометричні поверхні 28

9 Перетин поверхонь площиною та прямою.. 30

10 Взаємний перетин поверхонь. Розгортки. 32

11 Зображення: види, розрізи, перерізи, виносні елементи (ГОСТ 2.305-68) 36

12 Аксонометричні проекції 39

13 Проекції з числовими позначками. Пряма. Дві прямі 41

14 Проекції з числовими позначками. Площина. Взаємне положення двох площин, прямої та площини. 43

15 Топографічні поверхні 46

ЛІТЕРАТУРА.. 48

ВСТУП

Теоретичною основою інженерної графіки є нарисна геометрія, яка розглядає рішення математичних та інженерно-технічних задач за допомогою графічних методів. При цьому використовується метод проекціювання, який дозволяє отримати графічні зображення геометричних образів на три взаємно перпендикулярні площини проекцій П₁, П₂ і П₃.

Найбільш поширеним є ортогональне, або прямокутне проекціювання. При такому проекцію ванні з будь-якої точки геометричного образу, який знаходиться у просторі, проводять перпендикуляри до перетину з П₁, П₂ та П₃.

Таким чином отримують проекції різних точок, прямих, площин та інших геометричних елементів.

На основі аналізу проекцій, використання відповідних теоретичних положень та методик графічних побудов на кресленні отримують рішення вищезгаданих задач.

Для рішення кожної задачі необхідно:

1) вивчити відповідний теоретичний розділ курсу;

2) проаналізувати графічну умову задачі (визначити положення відносно П₁, П₂, П₃ та основні властивості проекцій кожного геометричного образу);

3) розробити план рішення задачі, виходячи з умови мінімальної кількості графічних побудов;

4) записати алгоритм рішення (послідовність операцій) задачі;

5) виконати необхідні побудови.

При написанні алгоритму слід використовувати наступні позначення та символи:

1) площини проекцій – горизонтальна П₁, фронтальна П₂, профільна П₃;

2) вісі проекцій – х, у, z;

3) позначення проекцій точок – горизонтальна А₁, фронтальна А₂, профільна А₃;

4) проекції точки А на вісі проекцій – A_x, A_y, A_z;

5) проекції відрізка прямої – А₁В₁, А₂В₂, А₃В₃;

6) h – горизонталь, f – фронталь, p – профільна пряма (прямі рівня);

7) прямі – a, b, c, d,…;

8) площини – А (альфа), Г (гамма), Δ (дельта), Σ (сигма), Θ (тета);

9) сліди площин – горизонтальний Г_П1, фронтальний - Г_П2, профільний - Г_П3;

10) належність - Ì, Î;

11) паралельність - ||;

12) перпендикулярність - ^;

13) дотичність –

14) мимобіжність –

15) співпадання - ≡;

16) пересічність - ∩, Х;

17) рівність, результат - =;

18) перетворення - ®;

19) еквівалентність – Û;

20) знак імплікації: якщо …, то … - Þ.

Ортогональні проекції точки

Механізм утворення проекції точки пояснює об’ємна модель (рис. 1). Для отримання проекцій точки А необхідно побудувати перпендикуляри до перетину з П₁, П₂, П₃.

Точки перетину перпендикулярів з П₁, П₂, П₃ визначають положення А₁, А₂, А₃. A_x, A_y, A_z – проекції точки А на вісі X, Y, Z.

На практиці використовують площинне креслення (епюр Монжа), яке отримують при суміщенні П₁ та П₃ з П₂ за напрямком стрілок (рис. 2).

Рис. 1 Рис. 2

Основні властивості площинного креслення Монжа (рис. 2):

1) А₂А₁^Х; 2) А₂А₃^Z; 3) |A₁A_X|=|A_ZA₃|=|AA₂|.

1.1 Побудувати проекції точок за їх координатами:

А(10;20;30); В(15;25;0); С(0;30;35); D(20;0;40);

E(25;0;0); F(0;35;0); K(0;0;0).

1.2 Побудувати проекції точки А` симетрично точці А відносно площини П₁.

1.3 Побудувати проекції L за координатами L(15;-20;30).

1.4 Побудувати відсутні проекції точок

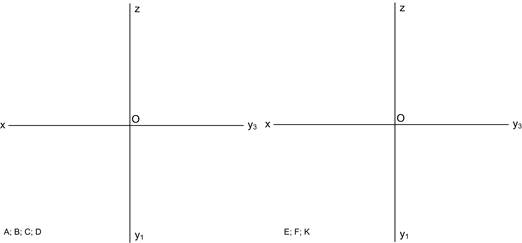
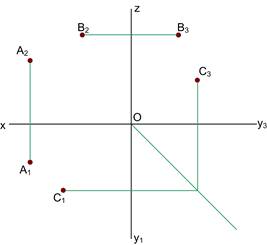
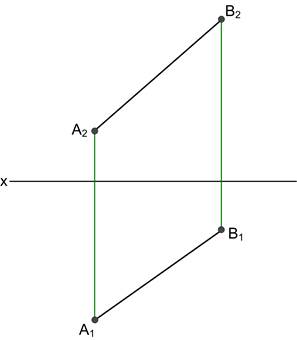
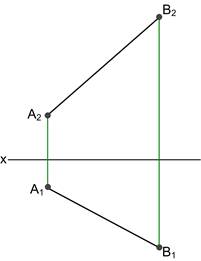
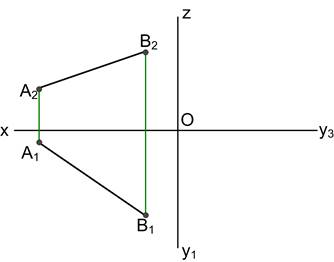
Ортогональні проекції прямої

Положення прямої визначається положенням двох точок цієї прямої.

В системі П₁, П₂, П₃ пряма може займати сім положень:

- загальне (не паралельне та не перпендикулярне до П₁, П₂, П₃);

- прямі рівня (h|| П₁; f|| П₂; p|| П₃);

- проекцюючі прямі (^П₁, ^П₂, ^П₃).

Точки перетину прямої з площинами проекцій називаються слідами прямої. Н – горизонтальний слід, F – фронтальний слід, Р – профільний слід.

Для визначення натуральної величини відрізка прямої використовують метод прямокутного трикутника.

Пропорційний поділ відрізка прямої виконують з використанням допоміжної прямої.

Точка належить до прямої, якщо її проекції розташовані на однойменних проекціях прямої.

2.1 Побудувати відсутні проекції прямих та визначити їх положення відносно П₁, П₂, П₃.

2.2 Визначити натуральну величину відрізка АВ, кути нахилу до П₁, П₂, а також побудувати сліди цієї прямої.

2.3 За заданими слідами побудувати проекції прямої CD та поділити її у співвідношенні 2:3.

2.4 На прямій АВ визначити точку К на відстані 20 мм від П₁ та точку D на відстані 30 мм від П₂.

2.5 Визначити чи належить точка А до прямої n.

2.6 На прямій АВ визначити точку С рівновіддалену від П₁ та П₂, точку D рівновіддалену від П₁ та П₃, точку Е рівновіддалену від П₂ та П₃.

Познавательные статьи:



Техника прыжка в длину с разбега

Организация работы процедурного кабинета

Области применения синхронных машин

Оптимизация по Винеру и Калману