
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рівняння прямої, що проходить через задану точку перпендикулярно даному вектору.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Знайдемо рівняння прямої, що проходить через задану точку М0(x0; y0) перпендикулярно даному ненульовому вектору
Рівняння (2.8) називається рівнянням прямої, що проходить через задану точку перпендикулярно заданому вектору. Вектор
де А і В — координати нормального вектора,
71) Розв’язування СЛАР за допомогою оберненої матриці (матричний спосіб). Коефіцієнти при невідомих запишемо у вигляді матриці, яку назвемо матрицею системи. Числа, що стоять в правих частинах рівнянь, утворюють стовпець, який називається стовпцем вільних членів. Якщо тепер через позначити стовпець із невідомих, то систему можна записати в матричному вигляді. Обернена матриця — для кожної невиродженої квадратної матриці
де Якщо для матриці 72) Розклад 2-вимірного та 3-вимірного вектора за базисними векторами. Зміст коефіцієнтів розкладу. Розглянемо n -вимірний многовид, вміщений в N -вимірний евклідовий простір (
Многовид в цьому просторі задається параметрично вектор-функцією:
Параметри
Розглянемо другу похідну
Дотичний вектор можна розкласти по базису
Коефіцієнти розкладу (числа Ми можемо формули (4) і (5) зібрати в одну формулу:
Розриви функції першого роду. Розриви функції другого роду. Точка розриву - це така точка (значення аргументу) в якій функція не є неперервною. Розрізняють такі види точок розриву: Розрив називають усувним, якщо в даній точці існує границя функції, що не збігається з значенням функції. Точку називають точкою розриву першого роду, якщо існують скінченні ліва та права границі в даній точці, та вони не збігаються. Якщо хоча б одна одностороння границя не існує, чи нескінченна, то точку називають точкою розриву другого роду. 74. Сформулювати умови рівності визначника нулю. Таблиця похідних елементарних функцій.
Теорема Кронеккера-Капеллі.
СЛАР має розв'язки тоді і тільки тоді,коли ранг її матриці Причому система має єдине рішення, якщо ранг дорівнює числу невідомих і нескінченно багато рішень, якщо ранг менше числа невідомих. Точки перегину функції. В математиці, точкою перегину, плоскої кривої називається точка кривої в якій змінюється знак кривизни. Якщо крива є графіком функції, то в цій точці опукла частина функції відділяється від вгнутої. Властивості
78.Скалярним добутком двох векторів називається число яке дорівнює сумі добутків відповідних кординат. 79. Два вектори ортогональні, якщо скалярний добуток цих векторів дорівнює нулю, тобто, кут між ними 90° або π/2 радіан. Таким чином, ортогональність векторів є узагальненням перпендикулярності. Умови паралельності прямих Теорема 1. Якщо при перетині двох прямих третьою виконується хоча б одна з таких умов: Фізичний зміст похідної Похідна від шляху-швидкість
|
||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 938; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.247.24 (0.006 с.) |

 .
. Візьмемо на прямій довільну точку M(x; у) і розглянемо вектор
Візьмемо на прямій довільну точку M(x; у) і розглянемо вектор  =(x–x0;у–y0), (див. рис. 21). Оскільки вектори
=(x–x0;у–y0), (див. рис. 21). Оскільки вектори  і
і  , тобто
, тобто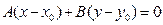 (2.8)
(2.8) (2.9)
(2.9) - вільний член. Рівняння (2.9) є загальне рівняння прямої (див. (2.4)).
- вільний член. Рівняння (2.9) є загальне рівняння прямої (див. (2.4)).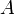 , розмірності
, розмірності 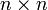 , завжди існує обернена матриця, позначається
, завжди існує обернена матриця, позначається  така що:
така що:
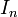 одинична
одинична  , то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки кожна оборотна матриця є невиродженою.
, то така матриця називається оборотною, тобто кожна невироджена матриця є оборотною, і навпаки кожна оборотна матриця є невиродженою. ). Точки евклідового простору будемо зображати радіус-вектором
). Точки евклідового простору будемо зображати радіус-вектором  , який в прямокутних декартових координатах має вигляд:
, який в прямокутних декартових координатах має вигляд:

 є координатами на многовиді. Часткові похідні радіус-вектора по цих координатах будуть дотичними векторами до многовиду і утворюють базис в дотичному афінному підпросторі евклідового простору.
є координатами на многовиді. Часткові похідні радіус-вектора по цих координатах будуть дотичними векторами до многовиду і утворюють базис в дотичному афінному підпросторі евклідового простору.
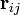 радіус-вектора многовида по параметрах. Це є вектор, який можна розкласти на два вектори - дотичний до многовиду
радіус-вектора многовида по параметрах. Це є вектор, який можна розкласти на два вектори - дотичний до многовиду  і перпендикулярний
і перпендикулярний  :
:
 :
:
 ) вивчав німецький математик Елвін Бруно Крістофель, тому вони називаються символами Крістофеля.
) вивчав німецький математик Елвін Бруно Крістофель, тому вони називаються символами Крістофеля.

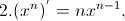


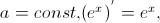








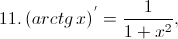




 ;
;


