
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нульова матриця в якій всі елементи рівні нулю.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дві матриці А і В називаються рівними (А = В), якщо вони однакового розміру (тобто мають однакову кількість рядків і однакову кількість стовбців та їхвідповідні елементи рівні). Так, якщо
то А=B, если a11=b11, a12=b12, a21=b21, a22=b22
29. Найбільше і найменше значення функції, поняття математичного аналізу. Значення, що приймається функцією в деякій точці безлічі, на якій ця функція задана, називається найбільшим (найменшим) на цій безлічі, якщо ні в якій іншій точці безлічі функція не має більшого (меншого) значення. Н. і н. з. ф. в порівнянні з її значеннями у всіх досить близьких крапках називаються екстремумами (відповідно максимумами і мінімумами) функції. Н. і н. з. ф., заданою на відрізку, можуть досягатися або в крапках, де похідна дорівнює нулю, або в крапках, де вона не існує, або на кінцях відрізання. Безперервна функція, задана на відрізку, обов'язково досягає на нім найбільшого і найменшого значень; якщо ж безперервну функцію розглядати на інтервалі (тобто відрізку з виключеними кінцями), то серед її значень на цьому інтервалі може не виявитися найбільшого або найменшого. Наприклад, функція в = x, задана на відрізку [0; 1], досягає найбільшого і найменшого значень відповідно при x = 1 і x = 0 (тобто на кінцях відрізання); якщо ж розглядати цю функцію на інтервалі (0; 1), то серед її значень на цьому інтервалі немає ні найбільшого, ні найменшого, оскільки для кожного x 0 завжди знайдеться точка цього інтервалу, лежача правіше (лівіше) x 0, і така, що значення функції в цій крапці буде більше (відповідно менше), ніж в точці x 0. Аналогічні твердження справедливі для функцій багатьох змінних.
30. Область визначення — множина допустимих значень аргументу функції. Позначається як D(y), якщо вказується область визначення функції y=f(x). Якщо задані: числова множина Тобто, визначення області значень є необхідною умовою визначення функції. Визначення. Значення змінних, на яких задається функція Визначення. Значення змінних, при яких алгебраїчний вираз
Визначення. Областю визначення рівняння Якщо функція задана формулою, то область визначення складається зі всіх значень незалежної змінної, при яких формула має зміст.
31. Обчислення оберненої матриці методом Жордана-Гауса. Метод Гауса полягає в приведенні розширеної матриці до верхнього трикутного виразу. Асимптота – це пряма, доякої крива при віддаленні в нескінченність наближається як завгодно близько
Геометричний вектор - величина, яка характеризується числовим значенням і напрямком. Число a називається границею функції f у точці x 0, якщо для як завгодно малого E>0 існує номер n0 , який залежить від E, тобто для всіх n=>n0 відстані між an та A<E
Графік функції - називається підмножина декартового добутку функція F (X), яка визначена в межах деякої точки х0, називається безперервною в точці х0, якщо межа функції та її значення в цій точці рівні. Обернена матриця — для кожної невиродженої квадратної матриці
де
Обернена функція (обернене відображення) до даної функції f — в математиці така функція g, яка в композиції з f дає тотожне відображення. п-вимірний вектор – система декількох випадкових величин. Похідна функціх в точці – це границя відношення її приросту до приросту аргументу за умови, що прирість аргументу прямую до нуля.
Означення розв’язку СЛАР. Розв'язати систему СЛАР – значить знайти такі значення невідомих
|
||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.9.175 (0.007 с.) |



 та правило
та правило  , що дозволяє поставити у відповідність кожному елементу
, що дозволяє поставити у відповідність кожному елементу  з множини
з множини  з областю визначення
з областю визначення  .
. має зміст, називають допустимими значеннями змінних. Множину всіх допустимих значень змінних називають областю допустимих значень змінних
має зміст, називають допустимими значеннями змінних. Множину всіх допустимих значень змінних називають областю допустимих значень змінних  .
. називають множину всіх тих значень зміної x, при яких алгебраїчні вирази
називають множину всіх тих значень зміної x, при яких алгебраїчні вирази  і
і 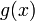 одночасно мають зміст.
одночасно мають зміст.


 (
( ), що містить всі пари (x, y), для яких f(x)=y, це малюнок, на якому можна побачити як змінюється значення Y в залежності від значення Х.
), що містить всі пари (x, y), для яких f(x)=y, це малюнок, на якому можна побачити як змінюється значення Y в залежності від значення Х. 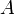 , розмірності
, розмірності 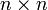 , завжди існує обернена матриця, позначається
, завжди існує обернена матриця, позначається  така що:
така що:
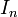 одинична
одинична 
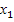 =
=  ,
, 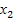 =
= 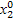 ,....
,.... 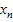 =
= 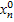 , при підстановці яких у систему СЛАР усі її рівняння обертаються у тотожність.
, при підстановці яких у систему СЛАР усі її рівняння обертаються у тотожність.


