
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Невырожденные матрицы. Обратная матрица. Ранг матрицы.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Невырожденной матрицей называется квадратная матрица Определение. Матрицей, союзной к матрице
где Напомним, что матрица
1.2.2. Обратная матрица Теорема ( единственности существования обратной матрицы): Если у матрицы Доказательство. Пусть существует матрица Тогда Значит, Для нахождения обратной матрицы 1.Найдем определитель матрицы 2.Составим союзную матрицу
3.Найдем произведение матриц
4.Составим обратную матрицу
Свойства обратной матрицы: 1. 2. 3. Пример. Найти обратную матрицу к матрице Решение. 1. Найдем 2. Найдем алгебраические дополнения для каждого элемента матрицы
Cоставим союзную матрицу
3. Найдем произведение матриц
Аналогично проверим, что
4. Составим обратную матрицу
1.2.3. Ранг матрицы Определение. В матрице, состоящей из Количество таких миноров определяется числами Предположим, что все определители некоторого порядка Определение. В матрице порядка Столбцы и строки матрицы, на которых стоит базисный минор, также называются базисными. Определение. Порядок базисного минора матрицы называется рангом матрицы и обозначается: Можно использовать и другое определение ранга матрицы. Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров. Если Ранг нулевой матрицы равен нулю, так как все миноры матрицы равны нулю.
Пример. Найти ранг матрицы Решение. Вычислим определитель матрицы Свойства ранга матрицы: 1. При транспонировании матрицы ее ранг не меняется. 2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится. 3. Ранг матрицы не изменяется при элементарных преобразованиях матрицы. Еще одним методом вычисления ранга матрицы размера Суть его в том, что для вычисления ранга матрицы нужно найти хотя бы один ее минор порядка Однако на практике часто поступают наоборот – переходят от миноров меньшего порядка к минорам большего порядка. Если найден минор -го порядка отличный от нуля, то вычисляют только миноры
Пример. Найти ранг матрицы Решение.
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 3780; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.135.82 (0.006 с.) |

 -го порядка, определитель которой отличен от нуля. В противном случае матрица называется вырожденной.
-го порядка, определитель которой отличен от нуля. В противном случае матрица называется вырожденной. , называется матрица
, называется матрица ,
, ij данной матрицы
ij данной матрицы  -1
-1 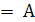 -1
-1  , где
, где  – единичная матрица того же порядка, что и матрица
– единичная матрица того же порядка, что и матрица  , то она единственна.
, то она единственна. , для которой
, для которой  и матрица
и матрица  , для которой
, для которой  .
. , то есть
, то есть  . Умножим обе части равенства на матрицу
. Умножим обе части равенства на матрицу  , где
, где  и
и  .
.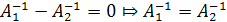 , что и требовалось доказать.
, что и требовалось доказать. и
и  Оно равно
Оно равно  и
и  .
.
 .
.
 .
. .
. .
.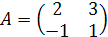 .
. , следовательно матрица
, следовательно матрица  :
: ,
,  ,
, ,
,  .
. .
. .
. :
: .
. .
. строк и
строк и  столбцов, вычеркнем некоторые строки и столбцы так, чтобы число оставшихся строк и столбцов стало одинаковым, например
столбцов, вычеркнем некоторые строки и столбцы так, чтобы число оставшихся строк и столбцов стало одинаковым, например  . Из этих строк и столбцов составим определитель. Этот определитель называется минором k-го порядка.
. Из этих строк и столбцов составим определитель. Этот определитель называется минором k-го порядка. . Наименьший порядок этих определителей равен единице, причем определители первого порядка суть сами элементы матрицы.
. Наименьший порядок этих определителей равен единице, причем определители первого порядка суть сами элементы матрицы. -го порядка также равны нулю, так как всякий определитель порядка
-го порядка также равны нулю, так как всякий определитель порядка  также будут равны нулю. Это значит, что если все определители -го порядка равны нулю, то и все определители большего порядка также равны нулю.
также будут равны нулю. Это значит, что если все определители -го порядка равны нулю, то и все определители большего порядка также равны нулю. минор порядка
минор порядка  называется базисным, если он не равен нулю, а все миноры порядка
называется базисным, если он не равен нулю, а все миноры порядка  и выше равны нулю, или не существуют вовсе, т.е.
и выше равны нулю, или не существуют вовсе, т.е.  совпадает с меньшим из чисел
совпадает с меньшим из чисел  или
или  .
. .
. .
. является метод окаймляющих миноров.
является метод окаймляющих миноров.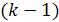 и так далее.
и так далее. , выполнив элементарные преобразования и получив эквивалентную матрицу.
, выполнив элементарные преобразования и получив эквивалентную матрицу.


 . В последней матрице есть минор 2-го порядка отличный от нуля,
. В последней матрице есть минор 2-го порядка отличный от нуля,  , значит
, значит  .
.


