
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы комбинаторики . Формула Бернулли.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Элементы комбинаторики. Если из множества, содержащего m элементов, требуется выбрать какие-то k элементов, то возникает вопрос: сколькими способами это можно сделать и какие подмножества при этом получаются. Такие задачи называются комбинаторными, а соответствующий раздел математики – комбинаторикой. Все формулы для подсчета числа решений в комбинаторных задачах опираются на правило произведения: если элемент X можно выбрать kспособами, а элемент Y можно выбрать n способами, то пару XY можно составить kn способами. Размещение с повторением. Из множества, содержащего m элементов, нужно выбрать k элементов, причем выбранный элемент, после того, как его взяли, вновь возвращается в исходное множество (то есть элементы в выбранном множестве могут повторяться). Пользуясь правилом произведения, получим, что каждый из k элементов может быть выбран m способами. Таким образом, общее число комбинаций равно Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7. Решение. Первой цифрой в числе может быть любая из четырех имеющихся. То же самое можно сказать и о последующих цифрах числа, поэтому общее число комбинаций: Размещение без повторений. Из множества, содержащего m различных элементов, надо выбрать упорядоченное подмножество из kэлементов (k£m), то есть такое подмножество, в котором элементы располагаются в определенном порядке, и изменение порядка элементов изменяет подмножество. Кроме этого, элементы в выбранном подмножестве не повторяются. Требуется выяснить, сколько таких комбинаций существует. По правилу произведения получаем, что первый элемент можно выбрать m способами, второй элемент – (m-1) способом, и так далее, а элемент с номером k можно выбрать (m – k + 1) способами. Следовательно, число упорядоченных k-элементных подмножеств, взятых из множества, содержащего m элементов равно m(m-1)(m-2)…(m-k+1). Такие подмножества называются размещениями из m элементов по k элементов, а их общее число можно выразить формулой Пример. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, при условии. Что цифры в числе не повторяются? Решение. Общее число комбинаций равно числу размещений из 6 элементов по 4: Перестановки. Пусть множество содержит m различных элементов. Рассмотрим все возможные варианты перестановок элементов этого множества. Получаемые при этом упорядоченные множества отличаются друг от друга только порядком входящих в них элементов. Такие упорядоченные множества называются перестановками. Число перестановок из m элементов равно:
Пример. Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5. 7, если цифры в числе не повторяются? Решение. Количество чисел равно числу перестановок из четырех элементов: Сочетания. Пусть из множества, содержащего m различных элементов, требуется выбрать подмножество, содержащее k различных элементов (k £ m). Получаемые при этом подмножества не упорядочены. Такие неупорядоченные подмножества называются сочетаниями. Число сочетаний изm элементов по k элементов вычисляется по формуле: Пример. В группе 10 студентов. Сколькими способами можно выбрать из этой группы троих студентов для участия в конференции? Решение. Число способов равно числу сочетаний из 10 элементов по 3 элемента: Формула Бернулли Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. Формула Бернулли. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р(0 < p < 1), событие наступит ровно k раз (безразлично, в какой последовательности), равна: Pn(k)=Cnkpkqn-k или
где q=1-p Вероятность того, что в n испытаниях событие наступит: а) менее k раз; б) более k раз; в) не менее k раз; г) не более k раз, — находят соответственно по формулам:
Pn(0)+Pn(1)+...+Pn(k-1); Pn(k+1)+Pn(k+2)+...+Pn(n); Pn(k)+Pn(k+1)+...+Pn(n); Pn(0)+Pn(1)+...+Pn(k);
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 922; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.36.91 (0.01 с.) |

 .
.
 .
.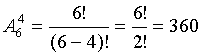



 .
.



