Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение производной; ее механический и геометрический смысл. Производная сложной, обратной , неявной функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Производная. Рассмотрим некоторую функцию y = f (x) в двух точках x 0 и x 0 +
Геометрический смысл производной. Рассмотрим график функции y = f (x):
Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точкуB, то Уравнение касательной. Выведем уравнение касательной к графику функции в точке A (x 0, f (x 0)). В общем случае уравнение прямой с угловым коэффициентом f ’(x 0) имеет вид: y = f ’(x 0) · x + b. Чтобы найти b,воспользуемся тем, что касательная проходит через точку A: f (x 0) = f ’(x 0) · x 0 + b, отсюда, b = f (x 0) – f ’(x 0) · x 0, и подставляя это выражение вместо b, мы получим уравнение касательной: y = f (x 0) + f ’(x 0) · (x – x 0). Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x (t) времени t. В течение интервала времени от t 0 до t 0 +
отсюда, v (t 0) = x’ (t 0), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v’ (t).
Пусть теперь задана сложная функция Теорема. Если Перейдем к рассмотрению производной обратной функции. Пусть на множестве Теорема. Если в точке Эта формула легко получается из геометрических соображений.
Если В обоих случаях Во многих задачах функция y (x) задана невным образом. Например, для приведенных ниже функций
невозможно получить зависимость y (x) в явном виде. Алгоритм вычисления производной y' (x) от неявной функции выглядит следующим образом:
• Решить полученное уравнение относительно производной y'(x).
|
|||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 721; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.220.221 (0.01 с.) |

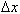 : f (x 0) и f (x 0 +
: f (x 0) и f (x 0 + 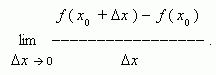

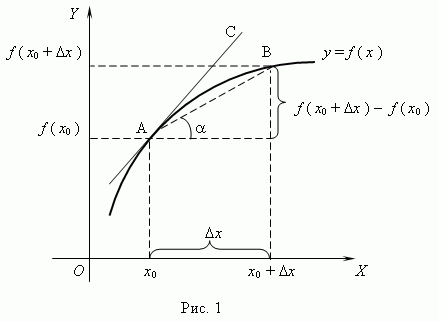
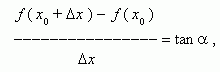
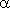 - угол наклона секущей AB.
- угол наклона секущей AB. точка перемещается на расстояние: x (t 0 +
точка перемещается на расстояние: x (t 0 +  0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v (t 0) материальной точки в момент времени t 0. Но по определению производной мы имеем:
0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v (t 0) материальной точки в момент времени t 0. Но по определению производной мы имеем: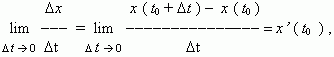
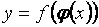 , т.е. переменная
, т.е. переменная 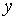 есть функция переменной
есть функция переменной 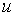
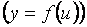 , а переменная
, а переменная 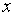 .
.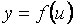 и
и 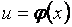 - дифференцируемые функции своих аргументов, то сложная функция
- дифференцируемые функции своих аргументов, то сложная функция 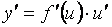 . Утверждение легко получается из очевидного равенства
. Утверждение легко получается из очевидного равенства  (справедливого при
(справедливого при  и
и  ) предельным переходом при
) предельным переходом при 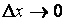 (что в силу непрерывности дифференцируемой функции влечет
(что в силу непрерывности дифференцируемой функции влечет  ).
).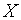 дифференцируемая функция
дифференцируемая функция 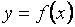 имеет множество значений
имеет множество значений 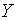 и на множестве
и на множестве  .
. производная
производная 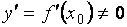 , то производная обратной функции
, то производная обратной функции 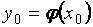 существует и равна обратной величине производной данной функции:
существует и равна обратной величине производной данной функции: 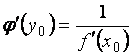 , или
, или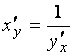 .
. Так как
Так как  есть тангенс угла наклона касательной линии
есть тангенс угла наклона касательной линии 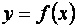 к оси
к оси  , то
, то 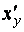 есть тангенс угла наклона той же касательной (той же линии
есть тангенс угла наклона той же касательной (той же линии 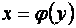 ) в той же точке
) в той же точке 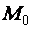 к оси
к оси  .
.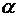 и
и 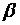 острые, то
острые, то 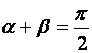 , а если тупые, то
, а если тупые, то 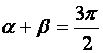 .
.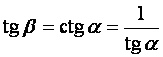 . Этому равенству и равносильно равенство
. Этому равенству и равносильно равенство