
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Генеральная совокупность и выборка. Вариационный ряд. Полигон и гистограммаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Статистической совокупностью называется совокупность объектов, одинаковых в каком-либо отношении, но в то же время обладающих варьирующими (изменчивыми) признаками. Вся исследуемая совокупность однородных объектов называется генеральной совокупностью. Множество из объектов, отобранных случайным образом из генеральной совокупности, называется выборочной совокупностью или выборкой. Число объектов, попавших в выборку, называется объемом выборки. Метод основанный на том, что по данным обследования выборки, взятой из генеральной совокупности, делается заключение о всей генеральной совокупности, называется выборочным методом. Выборка называется репрезентативной, если каждый элемент генеральной совокупности имеет одинаковую вероятность попасть в выборку.Если из генеральной совокупности отобрана выборка объема n, то количественное значение признака в этой выборке - это случайная величина, возможные значения которой обозначают символами X1, X2, …,Xk и называют вариантами. Числа ni объектов с одинаковыми значениями вариант называются частотами (весами) и обозначаются ni,n2,…,nk. Вариационный ряд. Последовательность значений вариант, расположенных в возрастающем порядке, называется вариационным рядом.Статистическим распределением называют вариационный ряд значений выборки и соответствующих им частот ni или относительных частот Wi.
Полигон и гистограмма. Полигоном частот (относительных частот) называется ломаная линия с вершинами в точках (xk , nk), где xk – варианта, nk – ее частота, или (xk , Wk), где Wk - относительная частота.Для непрерывных распределений более наглядное представление о характере распределения случайной величины дает гистограмма. Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников с основаниями длиной h и высотой ni/h, где h - длина каждого частичного интервала.Если соединить середины верхних прямоугольников гистограммы, то получим полигон частот. Числовые характеристики выборки. Для изучения основных свойств статистического распределения используют выборочные числовые характеристики. Для нахождения центра распределения вычисляют различные типы средних величин, моду и медиану, степени вариации - размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации и другие величины.
1. Выборочная средняя арифметическая:
2. Выборочная средняя квадратическая:
3. Выборочная средняя геометрическая:
При вычислении различных типов средних величин для одного и того же вариационного ряда всегда имеем
Эти неравенства характеризуют свойство мажорантности средних. Для упрощения вычисления выборочной средней арифметической удобно переходить от данных вариант Xi к условным вариантам 4. Модой М0 называется варианта, имеющая наибольшую частоту. 5. Медианой Ме называется такая варианта, которая делит вариационный ряд распределения на две равные части, т.е. варианта, находящаяся в середине ряда распределения.Если в дискретном вариационном ряду (2k+1) значений, то Me = xk+1. Если число вариант четное n = 2k, то медиана определяется как среднее арифметическое из двух серединных значений, т.е. 6. Размах вариации R определяется как разность между максимальным и минимальным вариантами, т.е.
7. Среднее линейное отклонение – это средняя арифметическая из абсолютных значений отклонений вариант от средней арифметической
8. Дисперсией называется средний квадрат отклонения всех значений признака от его средней величины.
Исправленная дисперсия
10. Среднее квадратическое отклонение равно квадратному корню из дисперсии:
Среднее квадратическое отклонение называют также стандартным отклонением. 11. Коэффициент вариации V - это выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 3588; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.63.108 (0.007 с.) |

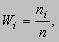
 .
.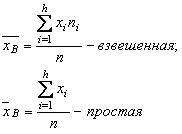 (1)
(1)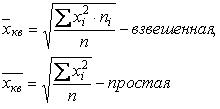 (2)
(2)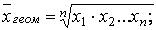 (3)
(3)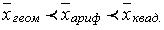
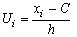 , где h - разность между соседними вариантами, C - ложный нуль (варианта с наибольшей частотой):
, где h - разность между соседними вариантами, C - ложный нуль (варианта с наибольшей частотой):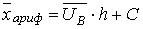 (4)
(4)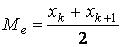 .
.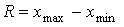 . (5)
. (5)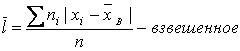 (6)
(6)
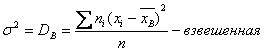 (7)
(7)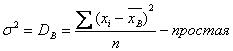
 (8)
(8) (9)
(9) (10)
(10)


