
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графическое представление вариационного ряда: полигон, гистограмма, кумулята.Содержание книги
Поиск на нашем сайте
Графическое представление вариационного ряда: полигон, гистограмма, кумулята. Для графич изображения вариационных рядов используются: 1.Полигон- служит для изображения дискретного вариационного ряда и представляет собой ломаную, в которой концы отрезков прямой имеют координаты (xi, ni), i=1,2,…,m. 2.Гистограмма- служит только для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака ki=xi+1- xi, i=1,2,…m, и высотами,равными частотам(частостям) ni (wi) интервалов. Если соединить середины верхних оснований проямоуг-ков отрезками прямой,то можн получить полигон того же распределения. 3.Кумулятивная кривая (кумулята)- кривая накопленных частот(частостей).Для дискретного ряда кумулята представляет ломаную,соединяющую точки (xi,niнак) или (xi,wiнак),i=1,2,…,m. Для интервального вариационного ряда ломаная начинается с точки,абсцисса которой равна началу первого интервала, а ордината –накопленной частоте(частости),равной нулю.Другие точки этой ломаной соответствуют концам итервалов.
Средняя арифметическая как мера центральной тенденции и её свойства. Средней арифметической вариационного ряда называется сумма произведений всех вариантов на соответствующие частоты, деленная на сумму частот:
Мода и её свойства. Мода — это наиболее часто встречающееся в определенной совокупности наблюдений значение переменной. При сгруппированных данных мода определяется как середина интервала группирования, содержащего наибольшее число значений наблюдаемой переменной. Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение(для которого вероятность pi или плотность вероятности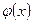 достигает максимума). Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках,распределение называется полимодльным. достигает максимума). Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках,распределение называется полимодльным.
26.Статистическая совокупность. Генеральная совокупность. Выборка. Репрезентативность выборки, таблица случайных чисел. Генеральная совокупн-ть- вся подлежащая изучению совокупность объектов(наблюдений). В математической статистике понятие генеральной совокупности трактуется как совокупность всех мыслимых наблюдений, которые могли бы быть произведены при данном реальном комплексе условий, и в этом смысле его не следует смешивать с реальными совокупностями, подлежащими статистическому изучению. Понятие генеральной совокупности аналогично понятию случайной величины(закону распределения вероятностей, вероятностному пространству), т к полностью обусловлено определенным комплексом условий. Та часть объектов,кот отобрана для для непосредственного изучения из генеральной совокуп-ти, называется выборочной совокупностью или выборкой. Сущность выборочного метода состоит в том,чтобы по некоторой части генеральной совокупности(по выборке) выносить суждение о ее св-вах в целом. Осн недостаток выборочного метода-ошибки исследования,называемые ошибками репрезентативности(представительства). Чтобы по данным выборки иметь возможность судить о генеральной совокупности, она должна быть отобрана случайно. Случайность отбора элементов в выборку достигается соблюдением принципа равной возможности всем элементам генеральной совокупности быть отобранными в выборку. На практике это достигается тем,что извлечение элементов в выборку проводится путем жеребьевки(лотереи) или с пом случайных чисел,имеющихся в специальн таблицах. Виды выборок: 1)собственно-случайная,образована случайным выбором элементов без расчленения на части или группы 2)механическая -в нее элементы из генеральной совокупности отбираются через определенный интервал.Н-р,если объем выборки должен составлять 10%,то отбирается каждый 10й ее элемент 3)типическая(стратифицированная)- в нее случайным образом отбираются элементы из типических групп,на которые по некоторому признаку разбивается генеральная совокупность 4)серийная(гнездовая) -в нее случайным образом отбираются не элементы а целые группы совокупности(серии), а сами серии подвергаются сплошному наблюдению.
Ц.П.Т. Ляпунова Пусть выполнены базовые предположения Ц.П.Т. Линдеберга. Пусть случайные величины { Xi } имеют конечный третий момент. Тогда определена последовательность
то
Если
Графическое представление вариационного ряда: полигон, гистограмма, кумулята. Для графич изображения вариационных рядов используются: 1.Полигон- служит для изображения дискретного вариационного ряда и представляет собой ломаную, в которой концы отрезков прямой имеют координаты (xi, ni), i=1,2,…,m. 2.Гистограмма- служит только для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака ki=xi+1- xi, i=1,2,…m, и высотами,равными частотам(частостям) ni (wi) интервалов. Если соединить середины верхних оснований проямоуг-ков отрезками прямой,то можн получить полигон того же распределения. 3.Кумулятивная кривая (кумулята)- кривая накопленных частот(частостей).Для дискретного ряда кумулята представляет ломаную,соединяющую точки (xi,niнак) или (xi,wiнак),i=1,2,…,m. Для интервального вариационного ряда ломаная начинается с точки,абсцисса которой равна началу первого интервала, а ордината –накопленной частоте(частости),равной нулю.Другие точки этой ломаной соответствуют концам итервалов.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 824; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.243 (0.008 с.) |


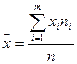 ,где xi-варианты дискретного ряда или середины интервалов интервального вариационного ряда; ni-соответствующие им частоты,m-число неповторяющихся вариантов или число интервалов;
,где xi-варианты дискретного ряда или середины интервалов интервального вариационного ряда; ni-соответствующие им частоты,m-число неповторяющихся вариантов или число интервалов; 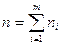 . Очевидно,что
. Очевидно,что 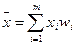 ,где
,где 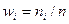 -частости вариантов или интервалов. Основные св-ва средней арифметической (аналогичны св-вам математичского ожидания случайной величины): 1. Средняя арифметич-кая постоянной равна самой постоятнной. 2. Если все варианты увеличить(уменьшить) в одно и то же число раз, то средняя арифметическая увеличится(уменьшится) во столько же раз:
-частости вариантов или интервалов. Основные св-ва средней арифметической (аналогичны св-вам математичского ожидания случайной величины): 1. Средняя арифметич-кая постоянной равна самой постоятнной. 2. Если все варианты увеличить(уменьшить) в одно и то же число раз, то средняя арифметическая увеличится(уменьшится) во столько же раз: 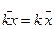 или
или  3. Если все варианты увеличить(уменьшить) на одно и то же число,то средняя арифметическая увеличится (уменьшится) на то же число:
3. Если все варианты увеличить(уменьшить) на одно и то же число,то средняя арифметическая увеличится (уменьшится) на то же число: 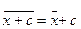 или
или 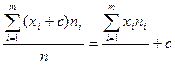 4. Средняя арифметическая отклонений вариантов от средней арифметической равна нулю:
4. Средняя арифметическая отклонений вариантов от средней арифметической равна нулю: 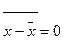 или
или 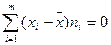 . При
. При 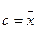
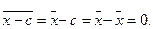 5. Средняя арифметическая алгебраической суммы нескольких признаков равна такой же сумме средних арифметических этих признаков:
5. Средняя арифметическая алгебраической суммы нескольких признаков равна такой же сумме средних арифметических этих признаков: 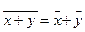 6. Если ряд состоит из нескольких групп, общая средняя равна средней арифметической групповых средних, причем весами являются объемы групп:
6. Если ряд состоит из нескольких групп, общая средняя равна средней арифметической групповых средних, причем весами являются объемы групп: 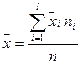 , где
, где 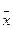 -общая средняя(средняя арифметическая всего ряда),
-общая средняя(средняя арифметическая всего ряда),  -групповая средняя i-й группы, объем которой равен ni., l – число групп.
-групповая средняя i-й группы, объем которой равен ni., l – число групп.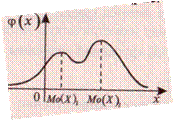
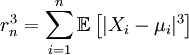 . Если предел
. Если предел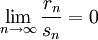 (условие Ляпунова),
(условие Ляпунова),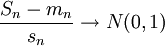 по распределению при
по распределению при 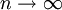 .
.



