
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциал функции. Производные и дифференциалы высших порядков.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Дифференциалом функции называется линейная относительно
Пусть производная некоторой функции f дифференцируема. Тогда производная от производной этой функции называется второй производной функции f и обозначается f". Таким образом, f" (x) = (f' (x)) '. Если дифференцируема (n - 1)-я производная функции f, то ее n -й производной называется производная от (n - 1)-й производной функции f и обозначается f(n). Итак, f(n) (x) = (f(n-1) (x)) ', n ϵ N, f(0) (x) = f (x). Число n называется порядком производной. Дифференциалом n -го порядка функции f называется дифференциал от дифференциала (n - 1)-го порядка этой же функции. Таким образом, dnf (x) = d (dn -1 f (x)), d 0 f (x) = f (x), n ϵ N. Если x - независимая переменная, то dx = const и d 2 x = d 3 x =... = dnx = 0. В этом случае справедлива формула dnf (x) = f (n)(x)(dx) n. Правило Лопиталя. Асимптоты, функции. Формула Лагранжа. Правило говорит, что если функции 1. 2. 3. тогда существует Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные. Вертикальной асимптотой графика функции
З акон больших числ. Вывариваное, нормальное, показательное распределения. Зако́н больши́х чи́сел в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости от вида сходимости различают слабый закон больших чисел, когда имеет место сходимость по вероятности, и усиленный закон больших чисел, когда имеет место сходимость почти всюду.Всегда найдётся такое конечное число испытаний, при котором с любой заданной наперёд вероятностью меньше 1 относительная частота появления некоторого события будет сколь угодно мало отличаться от его вероятности. Общий смысл закона больших чисел — совместное действие большого числа одинаковых и независимых случайных факторов приводит к результату, в пределе не зависящему от случая.
|
|||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 661; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.242.20 (0.008 с.) |

 часть приращения функции. Она обозначается как
часть приращения функции. Она обозначается как 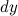 или
или 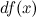 . Таким образом:
. Таким образом:
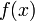 и
и  обладают следующим набором условий:
обладают следующим набором условий: или
или  ;
;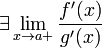 ;
; в некоторой окрестности точки
в некоторой окрестности точки  ,
, . При этом теорема верна и для других баз (для указанной будет приведено доказательство).
. При этом теорема верна и для других баз (для указанной будет приведено доказательство). называется вертикальная прямая
называется вертикальная прямая  , если
, если 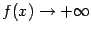 или
или  при каком-либо из условий:
при каком-либо из условий:  ,
, 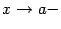 ,
, 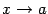 . Заметим, что мы при этом не требуем, чтобы точка
. Заметим, что мы при этом не требуем, чтобы точка 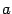 принадлежала области определения функции
принадлежала области определения функции  , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:
, однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: 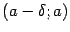 или
или  , где
, где  .
. 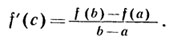
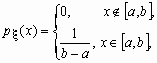

 ,
, 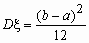 .
Экспоненциальное (показательное) распределение
Непрерывная случайная величина x имеет показательное распределение с параметром l > 0, если она принимает только неотрицательные значения, а ее плотность распределения px (x)и функция распределения Fx (x) имеют соответственно вид:
.
Экспоненциальное (показательное) распределение
Непрерывная случайная величина x имеет показательное распределение с параметром l > 0, если она принимает только неотрицательные значения, а ее плотность распределения px (x)и функция распределения Fx (x) имеют соответственно вид:
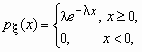

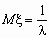 ,
, 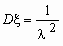 .
Нормальное распределение
Нормальное распределение играет исключительно важную роль в теории вероятностей и математической статистике.
Случайная величина x нормально распределена с параметрами a и s, s >0, если ее плотность распределения px (x) и функция распределения Fx (x) имеют соответственно вид:
.
Нормальное распределение
Нормальное распределение играет исключительно важную роль в теории вероятностей и математической статистике.
Случайная величина x нормально распределена с параметрами a и s, s >0, если ее плотность распределения px (x) и функция распределения Fx (x) имеют соответственно вид:
 ,
,  , Mx = a, Dx = s 2.
Часто используемая запись x ~ N (a, s) означает, что случайная величина x имеет нормальное распределение с параметрами a и s.
Говорят, что случайная величина x имеет стандартное нормальное распределение, если a = 0 и s = 1 (x ~ N (0, 1)). Плотность и функция распределения стандартного нормального распределения имеют вид:
, Mx = a, Dx = s 2.
Часто используемая запись x ~ N (a, s) означает, что случайная величина x имеет нормальное распределение с параметрами a и s.
Говорят, что случайная величина x имеет стандартное нормальное распределение, если a = 0 и s = 1 (x ~ N (0, 1)). Плотность и функция распределения стандартного нормального распределения имеют вид:
 ,
,  , Mx = 0, Dx = 1.
Здесь
, Mx = 0, Dx = 1.
Здесь  - функция Лапласа.
Функция распределения нормальной величины x ~ N (a, s) выражается через функцию Лапласа следующим образом:
- функция Лапласа.
Функция распределения нормальной величины x ~ N (a, s) выражается через функцию Лапласа следующим образом: 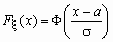 .
Если x ~ N (a, s), то случайную величину h = (x-a)/s называют стандартизованной или нормированной случайной величиной; h ~ N (0, 1) - имеет стандартное нормальное распределение
.
Если x ~ N (a, s), то случайную величину h = (x-a)/s называют стандартизованной или нормированной случайной величиной; h ~ N (0, 1) - имеет стандартное нормальное распределение



