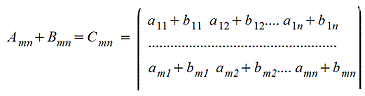Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование ррациональных, тригонометрических иррациональных функций.Содержание книги
Поиск на нашем сайте
Интегрирование рациональных функций - Функция Если Каждому действительному корню Каждому действительному корню Каждой паре комплексно сопряженных корней Каждой паре комплексно сопряженных корней кратности В приведенных выражениях Интегрирование иррациональных функций - Общий принцип интегрирования иррациональных выражений заключается в замене переменной, позволяющей избавиться от корней в подынтегральном выражении. Для некоторых классов функций эта цель достигается с помощью стандартных замен. Интегралы вида Интегралы вида Интегралы вида
Матрицы основные понятия. Действия над матрицами. Матрицей размера m на n (записывается так)называется совокупность mn вещественных (комплексных) чисел или элементов другой структуры (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа - номер строки и номер столбца.
Для обозначения матрицы используются прописные латинские буквы, при этом саму матрицу заключают в круглые или прямоугольные или в двойные прямые скобки. Элементы матрицы обозначают строчными латинскими буквами, снабженными двумя индексами: - элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n Действия над матрицами. 1. Сложение матриц - поэлементная операция
2. Вычитание матриц - поэлементная операция
3. Произведение матрицы на число - поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B) Amk*Bkn=Cmn причем каждый элемент сij матрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B, т.е.
Множества. Функция, основные понятия. Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т. д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников. Множества обычно обозначают большими буквами: A, B, C, N,..., а элементы этих множеств − аналогичными маленькими буквами: a, b, c, n,... Существуют стандартные обозначения для некоторых множеств.Функция (или Функциональная зависимость) – это зависимость переменной y от переменной x. Это такая зависимость, при которой каждому значению переменной x соответствует только одно значение переменной y.Переменную x называют независимой переменной или аргументом.Переменную y называют зависимой переменной или функцией от переменной x.Значение независимой переменной называют абсциссой (горизонтальная плоскость графика).Соответствующее значение зависимой переменной называется ординатой (вертикальная плоскость графика).Совокупность значений независимой переменной называется областью определения функции.Совокупность значений зависимой переменной называют областью значений функции.График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.Значения аргумента, при которых функция обращается в нуль, называют нулями функции.
|
||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 842; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.200.79 (0.007 с.) |

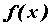 называется рациональной, если она вычисляется с помощью четырех арифметических действий, то есть в общем случае является частным от деления двух многочленов:
называется рациональной, если она вычисляется с помощью четырех арифметических действий, то есть в общем случае является частным от деления двух многочленов: 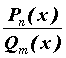 . Если
. Если 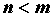 , рациональная дробь называется правильной. Неопределенный интеграл от рациональной функции всегда можно вычислить. Для этого:
, рациональная дробь называется правильной. Неопределенный интеграл от рациональной функции всегда можно вычислить. Для этого: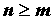 , выделяем целую часть рациональной дроби с помощью деления многочлена на многочлен. Правильную рациональную дробь (или правильный остаток от деления) раскладываем на простейшие дроби. Вид разложения определяется корнями многочлена
, выделяем целую часть рациональной дроби с помощью деления многочлена на многочлен. Правильную рациональную дробь (или правильный остаток от деления) раскладываем на простейшие дроби. Вид разложения определяется корнями многочлена 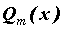 , а именно:
, а именно: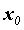 кратности 1 в разложении соответствует член
кратности 1 в разложении соответствует член  .
. в разложении соответствует набор из
в разложении соответствует набор из 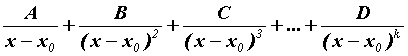 .
.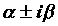 кратности 1 в разложении соответствует член
кратности 1 в разложении соответствует член  (
(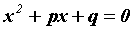 ).
).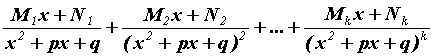 .
. - неопределенные коэффициенты, которые можно найти, приводя разложение обратно к общему знаменателю
- неопределенные коэффициенты, которые можно найти, приводя разложение обратно к общему знаменателю  к соответствующим коэффициентам
к соответствующим коэффициентам 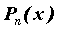 и решая систему относительно
и решая систему относительно 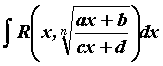 , где
, где  - рациональная функция своих аргументов, вычисляются заменой
- рациональная функция своих аргументов, вычисляются заменой 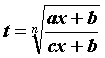 .
. вычисляются заменой
вычисляются заменой  или
или  .
.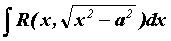 вычисляются заменой
вычисляются заменой  или
или 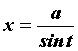 . Интегралы вида
. Интегралы вида 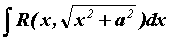 вычисляются заменой
вычисляются заменой  или
или 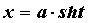 .
.