
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа 2. Предел. Производная.Содержание книги
Поиск на нашем сайте
Вариант 1 1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. Объем продукции цеха в течение рабочего дня представляет функцию
Вариант 2 1. Вычислить пределы, не пользуясь правилом Лопиталя
2.Найти производные функции:
3. Решить задачу. Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией
Вариант 3 1. Вычислить пределы, не пользуясь правилом Лопиталя
2.Найти производные функции:
3. Решить задачу. Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией
Вариант 4 1. Вычислить пределы, не пользуясь правилом Лопиталя
2.Найти производные функции:
3. Решить задачу. Тело, выпущенное вертикально вверх, движется по закону
Вариант 5 1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. По оси ОХ движутся две материальные точки, законы которых
Вариант 6 1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу: Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией
Вариант 7 1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. Зависимость между себестоимостью единицы продукции у и выпуском продукции х выражается функцией
Вариант 8 1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией
Вариант 9 1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. Тело, выпущенное вертикально вверх, движется по закону Вариант 10 1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. Объем продукции цеха в течение рабочего дня представляет функцию
Вариант 11 1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. Производитель реализует свою продукцию по цене р за единицу, а издержки при этом задаются зависимостью Вариант 12 1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. Зависимость между массой х кг вещества, получаемого в некоторой химической реакции и временем t выражается уравнением
Вариант 13 1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. Тело движется прямолинейно по закону
Вариант 14
1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу: Зависимость между массой х кг вещества, получаемого в некоторой химической реакции и временем t выражается уравнением
Вариант 15
1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу: Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией
Вариант 16
1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. Производитель реализует свою продукцию по цене р за единицу, а издержки при этом задаются зависимостью
Вариант 17
1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. Объем продукции цеха в течение рабочего дня представляет функцию
Вариант 18
1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. Количество электричества q (в кулонах), протекающее через поперечное сечение проводника, изменяется по закону
Вариант 19
1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу. Зависимость между массой х кг вещества, получаемого в некоторой химической реакции и временем t выражается уравнением
Вариант 20
1. Вычислить пределы, не пользуясь правилом Лопиталя:
2.Найти производные функции:
3. Решить задачу: Производитель реализует свою продукцию по цене р за единицу, а издержки при этом задаются зависимостью
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 333; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.183.77 (0.007 с.) |



 в)
в) 
 г)
г) 
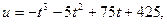 где t – время. Найти производительность труда за 2 часа до окончания работы, если рабочий день длится 5 часов.
где t – время. Найти производительность труда за 2 часа до окончания работы, если рабочий день длится 5 часов.
 в)
в) 
 г)
г) 
 . Определить средние и предельные издержки при объеме продукции 10 единиц
. Определить средние и предельные издержки при объеме продукции 10 единиц
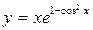 в)
в) 
 г)
г) 
 . Определить средние и предельные издержки при объеме продукции 5 единиц
. Определить средние и предельные издержки при объеме продукции 5 единиц
 в)
в) 
 г)
г) 
 . Определить скорость тела в момент соприкосновения с землей.
. Определить скорость тела в момент соприкосновения с землей.
 в)
в) 
 г)
г) 
 . С какой скоростью эти точки удаляются друг от друга с момента встречи?
. С какой скоростью эти точки удаляются друг от друга с момента встречи?
 в)
в) 
 г)
г) 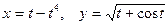

 в)
в) 
 г)
г) 
 . Найти эластичность себестоимости при выпуске продукции, равном 50.
. Найти эластичность себестоимости при выпуске продукции, равном 50.
 в)
в) 
 г)
г) 
 . Определить средние и предельные издержки при объеме продукции 5 единиц.
. Определить средние и предельные издержки при объеме продукции 5 единиц.
 в)
в) 
 г)
г) 

 в)
в) 
 г)
г) 
 где t – время. Найти производительность труда через 3 часа после начала работы и за час до окончания работы.
где t – время. Найти производительность труда через 3 часа после начала работы и за час до окончания работы.
 в)
в) 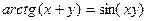
 г)
г) 
 . Найти оптимальный для производителя объем выпускаемой продукции.
. Найти оптимальный для производителя объем выпускаемой продукции.
 в)
в) 
 г)
г) 
 .Определить скорость реакции, когда t = 15 сек.
.Определить скорость реакции, когда t = 15 сек.
 в)
в) 
 г)
г) 
 . Найти скорость и ускорение тела в момент времени t = 6.
. Найти скорость и ускорение тела в момент времени t = 6.
 в)
в) 
 г)
г) 

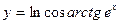 в)
в) 
 г)
г) 

 в)
в) 
 г)
г) 

 в)
в) 
 г)
г) 

 в)
в) 
 г)
г) 
 . Найти силу тока в конце четвертой секунды.
. Найти силу тока в конце четвертой секунды.
 в)
в) 
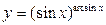 г)
г) 

 в)
в) 
 г)
г) 



