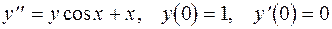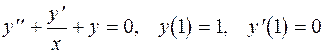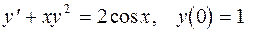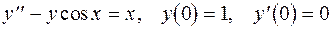Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения первого порядка.Содержание книги
Поиск на нашем сайте
Структура общего решения однородного дифференциального уравнения с постоянными коэффициентами:
Структура частного решения линейного неоднородного дифференциального уравнения с постоянными коэффициентами и специальной правой частью:
2. Задания для самостоятельной работы Задание 1. Найти решения дифференциальных уравнений первого порядка.
Задание 2. Найти общее решение дифференциального уравнения второго порядка, допускающего понижение порядка:
Задание 3. Решить задачу Коши: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20.
Задание 4. Решить линейное неоднородное дифференциальное уравнение:
Задание 5. Решить систему дифференциальных уравнений:
Зачетное задание №6. Числовые и функциональные ряды Справочный материал.
2. Задания для самостоятельной работы Задание1. Исследовать на сходимость:
Задание 2. Исследовать на абсолютную и условную сходимость:
Задание 3. Найти радиус сходимости и область сходимости степенных рядов
Задание 4. Вычислить приближенно значения определенных интегралов, взяв три члена разложения подынтегральной функции в ряд; указать погрешность
Задание 5. Найти разложение в степенной ряд решения 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.246.21 (0.011 с.) |






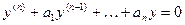





 - корень кратности «к»
- корень кратности «к»


 , f(x) =
, f(x) = 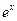 (
( )
)

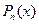

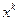







 )
)
 в)
в) 
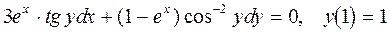 в)
в) 
 в)
в) 
 в)
в) 
 в)
в) 
 в)
в) 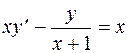
 в)
в) 
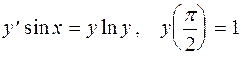 в)
в) 
 в)
в) 
 в)
в) 
 в)
в) 
 в)
в) 
 в)
в) 
 в)
в) 
 в)
в) 
 в)
в) 
 в)
в) 
 в)
в) 
 в)
в) 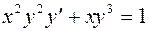

 в)
в) 
 в)
в)  в)
в)  в)
в)  в)
в)  б)
б)  в)
в) 
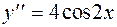 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
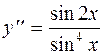 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б) 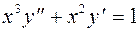 в)
в) 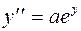
 б)
б)  в)
в) 
 б)
б)  в)
в) 
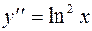 б)
б)  в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 
 в)
в) 
 б)
б)  в)
в) 
 б)
б)  в)
в) 















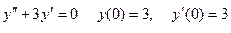
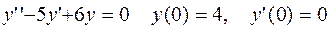



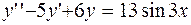




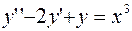




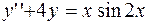
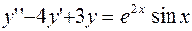


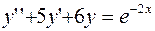


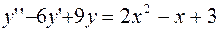












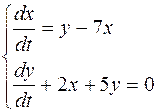
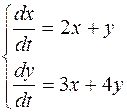


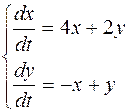




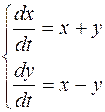
 .
.
 (1) и
(1) и  (2), если
(2), если 
 , то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) - расходимость ряда (2).
, то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) - расходимость ряда (2).
 , то оба ряда
, то оба ряда  одновременно сходятся или расходятся.
одновременно сходятся или расходятся.
 , то при
q < 1 ряд сходится,
q > 1 ряд расходится,
q = 1 признак ответа не дает.
, то при
q < 1 ряд сходится,
q > 1 ряд расходится,
q = 1 признак ответа не дает.
 , то при q < 1 ряд сходится, при q > 1 ряд расходится, а при q = 1 признак ответа не дает.
, то при q < 1 ряд сходится, при q > 1 ряд расходится, а при q = 1 признак ответа не дает.
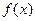 при х ³ 1 - непрерывная, положительная и монотонно убывающая функция, то ряд
при х ³ 1 - непрерывная, положительная и монотонно убывающая функция, то ряд  , где
, где  и несобственный интеграл
и несобственный интеграл  сходится или расходится одновременно
сходится или расходится одновременно
 сходится, если его члены, взятые по абсолютной величине, монотонно убывают и общий член
сходится, если его члены, взятые по абсолютной величине, монотонно убывают и общий член  при
при  т.е.:
1)
т.е.:
1)  2)
2) 

 .
Областью абсолютной сходимости степенного ряда является (-R; R)
.
Областью абсолютной сходимости степенного ряда является (-R; R)
 2.
2.  3.
3.  4.
4.  5.
5.  6.
6. 

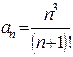







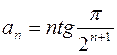



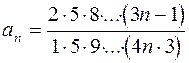











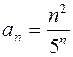

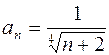


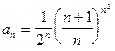


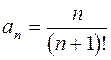








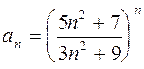














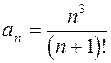











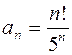









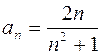







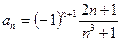
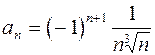





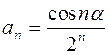



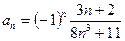











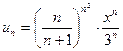
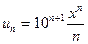


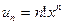














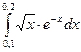







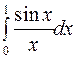


 дифференциального уравнения
дифференциального уравнения  , удовлетворяющего начальному условию
, удовлетворяющего начальному условию  .
.