
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа №1 по темеСодержание книги
Поиск на нашем сайте
"Векторная алгебра и аналитическая геометрия" Вариант №1 1.Выяснить образуют ли векторы 2. Найти вектор
3. Записать каноническое уравнение кривой и сделать чертеж. 4. Дан треугольник с вершинами в точках А(1,1), В(-2,3), С(4,7). Написать уравнение медианы, проведенной из вершины А.
Вариант №2 1. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 2. Вектор 3. Записать каноническое уравнение кривой и сделать чертеж.
4. Найти отрезки, отсекаемые на координатных осях плоскостью проходящей через точки А(3,1,1); В(1,4,1); С(1,1,7).
Вариант №3 1. Вектор осью OZ. Зная, что ½ 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3. Дан треугольник с вершинами в точках А(1,1), В(-2,3), С(4,7). Написать уравнение медианы, проведенной из вершины В.
4. Найти точку пересечения прямой и плоскости 3x-y+2z-5=0.
Вариант №4 1. Найти вектор х, коллинеарный вектору 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3. Построить линию, определяемую уравнением: 2x2 + 4y2 - 8x + 16y - 1 = 0. 4.Дан треугольник с вершинами в точках А(1,1), В(-2,3), С(4,7). Написать уравнение высоты, проведенной из вершины С.
Вариант №5 1. Вектор 2. Если векторы 3. Найти уравнение прямой, проходящей через точки А(2,-1,4) и В(3,2,-1) 4. Построить линию, определяемую уравнением: 2x2 + 4y2 - 16 = 0.
Вариант №6 1. Найти вектор 2. Выяснить, образуют ли векторы 3. Построить линию, определяемую уравнением: 2x2 - 4y2 + 16y = 0. 4. Составить уравнение прямой, проходящей через ось абсцисс и точку А(3,-2).
Вариант №7 1. Дан вектор:
2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3. Написать уравнение прямой, проходящей через точки А(1,1) и В(3,2). 4. Найти точку пересечения прямой x+y+z-5=0. Вариант №8 1. Дан вектор: 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3.. Построить линию, определяемую уравнением: x2 + y2 - 8x + 16y - 1 = 0. 4.Найти объем тетраэдра, ограниченного координатными плоскостями и плоскостями 2x-y+z-12-0.
Вариант №9 1. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 2. Построить линию, определяемую уравнением: 2x2 + 4y2 - 8x + 16y - 1 = 0. 3. Составить уравнение перпендикуляра, опущенного из точки М(2,3,-5) на плоскость 4x-2y+5z-12=0. 4. Выяснить, принадлежат ли точки А(-1,2), В(3,4), С(1,2) одной прямой.
Вариант №10 1.. Записать каноническое уравнение кривой Сделать чертеж. 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3. Найти объем параллелепипеда, построенного на векторах
4. Найти расстояние от точки А(1,2,1) до плоскости 2x-2y+z+6=0.
Вариант №11 1. Найти вектор х, если он параллелен 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3. Найти расстояние от точки К(1,2,3) до плоскости 2x-2y+z+6=0. 4. Записать каноническое уравнение кривой Сделать чертеж.
Вариант №12 1. Найти вектор х, удовлетворяющий условиям 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3. Вычислить высоту параллелограмма, построенного на векторах
4. Записать каноническое уравнение этой кривой и построить кривую, заданную уравнением Вариант №13 1. Записать каноническое уравнение кривой Сделать чертеж. 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3.Вычислить объем параллелепипеда, построенного на векторах
4. Дан треугольник с вершинами в точках А(-1,2), В(0,1) и С(1,4). Написать уравнение медианы, проходящей через вершину А. . Вариант №14 1. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 2. Найти угол между прямой 2х+3у-1=0 и прямой, проходящей через точки М1(-1,2), М2 (0,3).
3.Найти уравнение плоскости, проходящей через точку А(1,2,3), перпендикулярно оси OZ. 4. Записать каноническое уравнение кривой
Вариант №15 1. Записать каноническое уравнение кривой Сделать чертеж. 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3. Определить углы, образованные вектором 4. Найти угловой коэффициент и отрезок, отсекаемый на оси ординат прямой, проходящей через точки А(1,2) и В(-3,1).
Вариант №16 1. Найти вектор 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3. Определить объем параллелепипеда, построенного на векторах
4. Записать каноническое уравнение и построить кривую
Вариант №17 1. Найти уравнение прямой, проходящей через точку М(-1,3) и точку пересечения прямых 2х-у-1=0, 3х+у-4=0. 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3. Записать каноническое уравнение кривой Сделать чертеж. 4. Найти отрезки, отсекаемые на координатных осях плоскостью, проходящей через точки А(3,1,1), В(1,4,1), С(1,1,7). Вариант №18 1. Найти уравнение прямой, проходящей через точку А(1,-1) параллельно прямой, соединяющей точки М1(2,-3), М2 (5,1). 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3. Известны вершины пирамиды А(0,0,0), И(3,2,-1), С(2,3,2), Д(4,0,-3). Вычислить объем пирамиды и высоту. 4. Записать каноническое уравнение и построить линию
Вариант №19 1. Дан треугольник с вершинами в точках А(1,5), В(-4,3), С(2,9). Найти уравнение высоты, проведенной из вершины А. 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3. Составить уравнение плоскости, параллельной плоскости 3x-6y+4z-12=0, и проходящей через точку А(4,6,5). 4. Составить уравнение прямой, проходящей через точки А(-2,8,7) и В(6,8,9).
Вариант №20 1. Написать уравнение прямой, проходящей через точку М(4,3) перпендикулярно к вектору 2. Выяснить, образуют ли векторы базис? Если да, разложить по нему вектор 3. Найти расстояние от точки А(1,2,2) до плоскости 2x-3y+4z+12=0. 4.Записать каноническое уравнение и построить кривую
|
||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.183.104 (0.011 с.) |

 базис? Если да, то разложить по нему вектор
базис? Если да, то разложить по нему вектор  .
.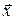 , зная, что он параллелен вектору
, зная, что он параллелен вектору и удовлетворяет условию
и удовлетворяет условию  .
.
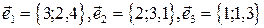
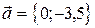 .
. параллелен вектору a={2,-1, 3}, образует острый угол с осью OX. Зная, что
параллелен вектору a={2,-1, 3}, образует острый угол с осью OX. Зная, что  =14, найти его координаты.
=14, найти его координаты.
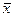 коллинеарен вектору
коллинеарен вектору  ={6;-8;-7,5}, образует острый угол с
={6;-8;-7,5}, образует острый угол с
 .
.
 и удовлетворяющий условию
и удовлетворяющий условию 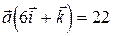 .
.
 .
. и
и  образует с осью ОУ тупой угол. Найти координаты вектора
образует с осью ОУ тупой угол. Найти координаты вектора  образуют базис, то разложите по нему вектор
образуют базис, то разложите по нему вектор 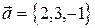 и
и  и удовлетворяет условию
и удовлетворяет условию 
 базис? Если да, разложить по нему вектор
базис? Если да, разложить по нему вектор  .
. . Найти вектор
. Найти вектор 

 .
. и плоскости
и плоскости . Найти вектор
. Найти вектор 

 .
.
 .
. .
.
 .
.
 и удовлетворяет условию
и удовлетворяет условию  .
.
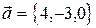 .
. .
. если
если 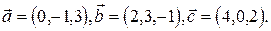

 .
. .
. .
. .
.
 .
.

 .
. . Сделать чертеж.
. Сделать чертеж.
 .
. c координатными осями.
c координатными осями. и удовлетворяющий условию
и удовлетворяющий условию 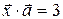 .
.
 .
.
 .
.
 .
. .
. .
. .
.
 .
. , если М1(0,-2), М2 (3,5).
, если М1(0,-2), М2 (3,5). .
.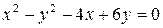 .
.


