
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие дифференциала функции.Содержание книги
Поиск на нашем сайте
Главная линейная относительно
Дифференциал независимой переменной x равен 2. Задания для самостоятельной работы.
Задание 1. Вычислить пределы:
Задание 3. Исследовать функцию на непрерывность и построить график.
Задание 4. Найти производные функции. В случаях а) и г) найти производные второго порядка.
Задание 5. Составить уравнение касательной и нормали к кривой в точке, соответствующей параметру t=t 0.
Задание 6. Решить задачу: 6.1. Объем продукции цеха в течение рабочего дня представляет функцию 6.2. Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией 6.3. Зависимость между себестоимостью единицы продукции у и выпуском продукции х выражается функцией 6.4. Производитель реализует свою продукцию по цене р за единицу, а издержки при этом задаются зависимостью
6.5. Объем продукции цеха в течение рабочего дня представляет функцию 6.6. Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией 6.7. Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией 6.8. Тело, выпущенное вертикально вверх, движется по закону 6.9. По оси ОХ движутся две материальные точки, законы которых 6.10. Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией 6.11. Зависимость между себестоимостью единицы продукции у и выпуском продукции х выражается функцией 6.12. Производитель реализует свою продукцию по цене р за единицу, а издержки при этом задаются зависимостью 6.14. Зависимость между массой х кг вещества, получаемого в некоторой химической реакции и временем t выражается уравнением 6.15. Объем продукции цеха в течение рабочего дня представляет функцию 6.16. Производитель реализует свою продукцию по цене р за единицу, а издержки при этом задаются зависимостью 6.17. Объем продукции цеха в течение рабочего дня представляет функцию 6.18 Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией
6.19 Зависимость между массой х кг вещества, получаемого в некоторой химической реакции и временем t выражается уравнением 6.20. Производитель реализует свою продукцию по цене р за единицу, а издержки при этом задаются зависимостью
Задание 7. Провести исследование и построить график функции.
Зачетное задание №3 Дифференцирование и интегрирование функции нескольких переменных Справочный материал.
2. Задания для самостоятельной работы. Задание1. Дана функция Z= f (x, y). Найти частные производные 1 и 2 порядка.
Задание 2. Найти наибольшее и наименьшее значение функции в замкнутой области Д.
Задание 3. Даны функция Z = Z (x, y), точка А (х 0, у 0) и вектор 1) grad Z в точке А; 2) производную в точке А по направлению вектора
Задание 4. Изменить порядок интегрирования. 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8. 1.9 1.10 1.11 1.12 1.13 1.14 1.15 1.16
1.17 1.18 1.19 1.20
Задание 5. Вычислить двойной интеграл. 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 2.10 2.11 2.12 2.13 2.14 2.16 2.17 2.18 2.19 2.20
Задание 6. Найти площадь фигуры, ограниченной данными линиями. 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 3.10 3.11 3.12 3.13 3.14 3.15 3.16 3.17 3.18 3.19 3.20
Зачетное задание №4 Интегралы Справочный материал
НЕОПРЕДЕЛЕННЫй ИНТЕГРАЛ. Основные свойства неопределенного интеграла. 1). 2). 3). 4). 5) Таблица основных производных и интегралов
методы интегрирования.
1. Интегрирование подстановкой
2. Интегрирование методом интегрирования по частям
Типы интегралов, берущиеся интегрированием по частям:
Интегрирование рациональных алгебраических функций:
1.Если подынтегральная дробь неправильная, то нужно выделить целую часть.
2. Если дробь правильная, то нужно применить разложение правильной дроби на простейшие дроби:
Интегрирование тригонометрических функций:
1. Используемые формулы:
Примеры:
2.Используемые формулы:
Пример:
3.Универсальная тригонометрическая подстановка:
Пример:
4. Если под интегралом
5.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.23.37 (0.01 с.) |

 часть приращения дифференцируемой функции называется дифференциалом функции в точке x, соответствующим приращению аргумента
часть приращения дифференцируемой функции называется дифференциалом функции в точке x, соответствующим приращению аргумента  .
.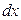 =
=  .
.
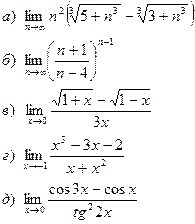


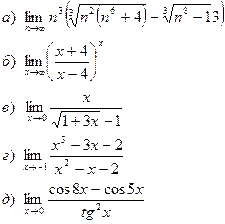















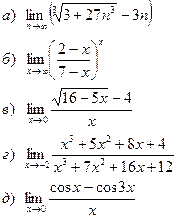









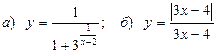






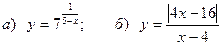



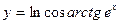 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
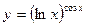 г)
г) 
 в)
в) 
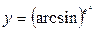 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
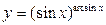 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
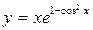 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 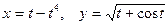
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 
 в)
в) 
 г)
г) 


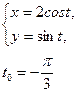

















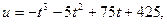 где t – время. Найти производительность труда через 2 часа после начала работы и за 2 часа до окончания работы.
где t – время. Найти производительность труда через 2 часа после начала работы и за 2 часа до окончания работы. . Определить средние и предельные издержки при объеме продукции 10 единиц.
. Определить средние и предельные издержки при объеме продукции 10 единиц. . Найти эластичность себестоимости при выпуске продукции, равном 60.
. Найти эластичность себестоимости при выпуске продукции, равном 60. . Найти оптимальный для производителя объем выпускаемой продукции.
. Найти оптимальный для производителя объем выпускаемой продукции. . Определить средние и предельные издержки при объеме продукции 5 единиц.
. Определить средние и предельные издержки при объеме продукции 5 единиц. . Определить скорость тела в момент соприкосновения с землей.
. Определить скорость тела в момент соприкосновения с землей. . С какой скоростью эти точки удаляются друг от друга с момента встречи?
. С какой скоростью эти точки удаляются друг от друга с момента встречи? .Определить скорость реакции, когда t = 10 сек.
.Определить скорость реакции, когда t = 10 сек. где t – время. Найти производительность труда через 3 часа после начала работы и за час до окончания работы.
где t – время. Найти производительность труда через 3 часа после начала работы и за час до окончания работы. . Определить средние и предельные издержки при объеме продукции 8 единиц.
. Определить средние и предельные издержки при объеме продукции 8 единиц.






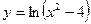











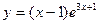


 .
.
 ,
, 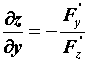 .
.

 где
где 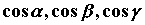 - направляющие косинусы вектора
- направляющие косинусы вектора  .
.




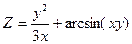


















 ,
,
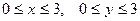


 ,
,

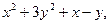
























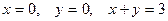








 . Найти:
. Найти:
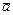 =
=













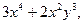



















 ,
,

 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.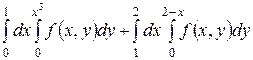 .
.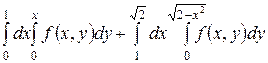 .
. .
. .
. .
. .
. .
.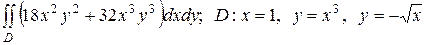 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.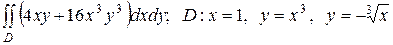 .
. .
. .
. .
.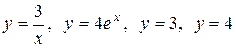 .
.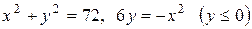 .
. .
. .
. .
. .
. .
. .
. .
. ..
.. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.
 ;
; ;
; ;
; , где
, где 
 - свойство инвариантности
- свойство инвариантности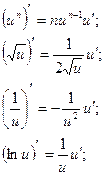





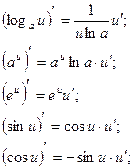
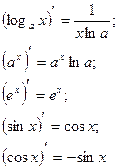







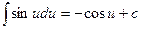










 .
. .
.
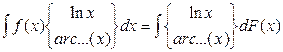
 ,
, 

 ,
,  ,
, 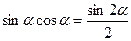 .
. ,
,  ,
,  .
. ,
, ,
,
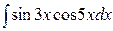 .
.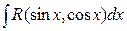 - подстановкой
- подстановкой  , тогда
, тогда 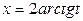 ,
, ,
,  ,
, 
 .
. и
и  содержатся только в четных степенях, то лучше применять подстановку:
содержатся только в четных степенях, то лучше применять подстановку: , тогда
, тогда  ,
,  ,
,  ,
, 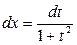
 - подстановкой
- подстановкой 


