Методические материалы по курсу «Высшая математика»

(Сборник контрольных работ и заданий для самостоятельной работы студентов экономических специальностей)

 

Калининград 2006

 

 

Методические материалы по курсу «Высшая математика» (Сборник контрольных работ и заданий для самостоятельной работы студентов экономических специальностей)- Калининград: БИЭФ, 2006. – с.

 

Авторы: Карлов А.М., Кикоть Е.Н., Зубарева Н.П.

Рецензент: Фунтикова Т.А. кандидат физико-математических наук, доцент кафедры дифференциальной геометрии и топологии РГПУ им. И.Канта, Жарикова Л. кандидат физико-математических наук, доцент кафедры высшей математики БИЭФ

 

Пособие содержит задания для самостоятельной домашней работы и контрольные работы по основным темам курса высшей математики. Предназначено для текущего контроля знаний студентов.

 

Для студентов и преподавателей математики.

 

 

Ó Балтийский институт экономики и финансов та, 2006

 

Содержание

 

Введение ……………………………………………………………….…………

I.Задания для самостоятельной работы

1. Зачетное задание №1. Элементы линейной и векторной алгебры, элементы аналитической геометрии …………………………………………

1.1 Справочный материал…………………………………………………..

1.2. Задания для самостоятельной работы ………………………………….

2. Зачетное задание №2 Предел и непрерывность функции одной переменной. Производная. Исследование функции и построение графика.

2.1 Справочный материал…………………………………………………..

2.2. Задания для самостоятельной работы ………………………………….

3. Зачетное задание №3 Дифференцирование и интегрирование функции нескольких переменных

3.1 Справочный материал…………………………………………………..

3.2. Задания для самостоятельной работы ………………………………….

4. Зачетное задание №4 Интегралы

4.1 Справочный материал…………………………………………………..

4.2. Задания для самостоятельной работы ………………………………….

5. Зачетное задание №5 Дифференциальные уравнения

5.1 Справочный материал…………………………………………………..

5.2. Задания для самостоятельной работы ………………………………….

6. Зачетное задание №6 Числовые и функциональные ряды

6.1 Справочный материал…………………………………………………..

6.2. Задания для самостоятельной работы

II. Контрольные работы

1. Контрольная работа №1 Векторная алгебра и аналитическая геометрия…………………………………………………………………..

2. Контрольная работа 2. Предел. Производная……………………..

Контрольная работа №3 Неопределенный и определенный интегралы

Контрольная работа №4 Дифференциальные уравнения

Список литературы…………………………………………………………

 

 

Введение

Настоящее пособие содержит методические указания, краткий теоретический материал, индивидуальные задания для самостоятельной работы и контрольные задания по курсу высшей математики. Представлены разделы: «Линейная алгебра и аналитическая геометрия», «Дифференциальное исчисление функции одной и нескольких переменных», «Интегральное исчисление функции одной и нескольких переменных», «Дифференциальные уравнения», «Числовые и степенные ряды».

 

 

 

 

Зачетное задание №1. Элементы линейной и векторной алгебры,

Элементы аналитической геометрии

Справочный материал.

Исследование системы m линейных уравнений с n переменными.

r<m Уравнения системы зависимые

r=m Уравнения системы независимые

 

 

УМНОЖЕНИЕ ВЕКТОРОВ

Произведение	Определение	Обозначение	Законы	Равенство нулю	Выражение в декартовых координатах
Скалярное	Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними: ав = | а | | в | соsφ= | а | пр ав = =| в | пр ва	ав = а · в = (а, в)	1. ав = ва; 2. а (в + с) = ав +ас; 3. (λ а) в = λ (а в); 4. а^2 = а а = | а | | а | соs0 = | а |^2.	а в = ׀ а ׀ ׀ в ׀ соsφ = 0 < => соsφ = 0 => φ = π/2 => а ┴ в	i i = j j = k k =1 i j = i k = j k = 0. Если а = (а1, а2, а3) в = (в1, в2, в3), то ав = а1·в1 + а2·в2 + а3·в3.
Векторное	Векторным произведением двух векторов а и в называется третий вектор с, удовлетворяющий условиям: 1. с ┴ а, с ┴ в; 2. (а, в, с) – правая тройка векторов; 3. | с | = | а х в | = | а | | в |sinφ= S параллелограмма, построен-ного на векторах а и в	а х в = [ а, в ]	1. а х в = - (в х а)   2. (а + в) х с = а х с + в х с – 3. (α а) х в = α (а х в)	а х в = 0,   | а х в | = | а | | в |sinφ = 0 <=> <=>sinφ = 0,   => а ║ в.	i x i = j x j = = k x k = 0. а х в=
Смешанное	Смешанным произведением векторов а, в, с называется скалярное произведение вектора а на векторное произведение векторов в и с.	(а, в, с) = а (в х с) = = а [ в,с ] = авс.	1. авс = вса = сав = - вас = - сав = - асв; 2. а (в + d) с = авс +аdс; 3. а (λ в) с = ав (λ с) = λ (авс)	авс = 0 <=> векторы а, в, с – компланарны,	авс =   | авс | = Vпар-да, построен-ного на векторах а, в, с.

УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ

Название	Уравнение	Обозначения
1. Общее уравнение		- нормальные векторы плоскости.
2. Каноническое		- направляющий вектор.
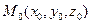3. Параметрическое		- точка на прямой. - направляющий вектор.
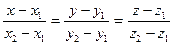
4. Уравнение прямой, проходящей через две точки М1 и М2		и 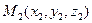- точки на прямой