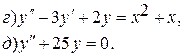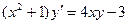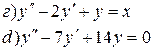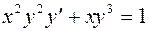Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Контрольная работа №3 Неопределенный и определенный интегралыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вариант №1
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить площадь плоской фигуры, ограниченной линиями
Вариант №2 1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить площадь плоской фигуры, ограниченной линиями
Вариант №3
1. Вычислить неопределенные интегралы:
Вычислить определенные интегралы:
3. Вычислить площадь плоской фигуры, ограниченной линиями
Вариант №4 1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить объем тела вращения вокруг оси ох фигуры, ограниченной линиями
Вариант №5
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
Вычислить площадь плоской фигуры, ограниченной
Вариант №6
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить площадь плоской фигуры, ограниченной линиями
Вариант №7
1. Вычислить неопределенные интегралы:
Вычислить определенные интегралы:
3. Вычислить объем тела вращения вокруг оси ох фигуры, ограниченной линиями
Вариант №8
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить объем тела вращения вокруг оси ох фигуры, ограниченной линиями
Вариант №9
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
Вычислить площадь плоской фигуры, ограниченной
Вариант №10
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить площадь плоской фигуры, ограниченной кривой
Вариант №11
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить площадь плоской фигуры, ограниченной параболой
Вариант №12
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить объем тела вращения вокруг оси ох фигуры, ограниченной линиями
Вариант №13
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить площадь плоской фигуры, ограниченной линиями
Вариант №14
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить объем тела вращения вокруг оси ох фигуры, ограниченной параболами
Вариант №15
1. Вычислить неопределенные интегралы:
Вычислить определенные интегралы:
3.Вычислить объем тела вращения, ограниченного линиями
Вариант №16
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить длину дуги кривой
Вариант №17
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить объем тела вращения
Вариант №18
1. Вычислить неопределенные интегралы:
Вычислить определенные интегралы:
3. Вычислить объем тела вращения
Вариант №19
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3.Вычислить объем тела вращения вокруг оси ох фигуры, ограниченной линиями
Вариант №20
1. Вычислить неопределенные интегралы:
2. Вычислить определенные интегралы:
3. Вычислить объем тела вращения
Контрольная работа №4 Дифференциальные уравнения
Вариант №1 1. Найти интегральную кривую уравнения 2. Решить дифференциальные уравнения: а) б) в)
Вариант №2 1. Найти уравнение касательной к интегральной кривой уравнения 2. Решить дифференциальные уравнения: а) б) в)
Вариант №3 1. Найти кривую, у которой длина отрезка нормали постоянна и равна 2. 2. Решить дифференциальные уравнения: а) б) в)
Вариант №4 1. Найти семейство кривых, подкасательная в любой точке которых есть среднее арифметическое координат точки касания. 2. Решить дифференциальные уравнения: a) б) в)
Вариант №5 1. Найти такую кривую, проходящую через точку М(0,3), чтобы угловой коэффициент касательной в любой ее точке равнялся ординате этой точки, уменьшенной на две единицы.
2. Решить дифференциальные уравнения: а) б) в)
Вариант №6 1. Найти кривую, отрезок касательной которой, отсекаемый от оси ОХ равен ординате точки касания. 2. Решить дифференциальные уравнения: а) б) в)
Вариант №7 1. Составить уравнение кривой, проходящей через начало координат, зная, что длина отрезка ее нормали равна абсциссе точки касания.
2. Решить дифференциальные уравнения: a) б) в)
Вариант №8 1.Найти интегральную кривую уравнения 2. Решить дифференциальные уравнения: a) б) в)
Вариант №9 1. Найти кривую, проходящую через точку М(-1,1), если угловой коэффициент касательной к ней в любой точке равен абсциссе точки касания. 2. Решить дифференциальные уравнения: а) б) в)
Вариант №10
1.Найти кривую, проходящую через точку М(-1,1), если угловой коэффициент касательной к ней в любой точке равен квадрату абсциссы точки касания.
2.Решить дифференциальные уравнения: а) б) в)
Вариант №11 1. Найти уравнение кривой, пересекающей ось абсцисс в точке х=1 и обладающей таким свойством: длина поднормали в каждой точке кривой равна среднему арифметическому координат этой точки кривой. 2. Решить дифференциальные уравнения: а) б) в)
Вариант №12 1. Найти кривую, для которой радиус-вектор равен длине отрезка касательной между точкой касания и осью Ох. 2. Решить дифференциальные уравнения: а) б) в)
Вариант №13 1. Найти интегральную кривую уравнения
2. Решить дифференциальные уравнения: а) б) в)
Вариант №14 1.Найти кривую, проходящую через точку М(-1,1), если угловой коэффициент касательной к ней в любой точке равен квадрату ординаты точки касания.
2. Решить дифференциальные уравнения: а) б) в)
Вариант №15
1.Найти кривую, проходящую через точку М(-1,1), если угловой коэффициент касательной к ней в любой точке равен ординате точки касания.
2. Решить дифференциальные уравнения: а) б) в)
Вариант №16 1.Найти кривую, проходящую через точку М(-1,1), если угловой коэффициент касательной к ней в любой точке равен сумме абсциссы и ординаты точки касания.
2. Решить дифференциальные уравнения:
a) б) в)
Вариант №17 1.Найти кривую, проходящую через точку М(-1,1), если угловой коэффициент касательной к ней в любой точке равен половине абсциссы точки касания. 3. Решить дифференциальные уравнения: а) б) в)
Вариант №18 1. Найти кривую, у которой угловой коэффициент касательной в любой точке равен произведению координат точки касания. 2. Решить дифференциальные уравнения: а) б) в)
Вариант №19 1. Найти кривую, проходящую через точку (-1,1), если угловой коэффициент касательной к ней в любой точке кривой равен половине ординаты точки касания. 2. Решить дифференциальные уравнения: а) б) в)
Вариант №20 1. Найти кривую, проходящую через точку (-1,-2), если поднормаль ее в каждой точке равна 2. 2. Решить дифференциальные уравнения: а) б) в)
|
||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 427; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.198.181 (0.012 с.) |





















 между точками их пересечения.
между точками их пересечения.

 между точками их пересечения.
между точками их пересечения.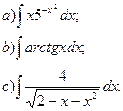
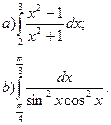






 и осью абсцисс.
и осью абсцисс.







 между точками их пересечения.
между точками их пересечения.

 вокруг оси ох.
вокруг оси ох.

 между точками пересечения ее с осью Ох.
между точками пересечения ее с осью Ох.
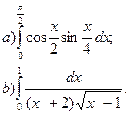
 вокруг оси оу
вокруг оси оу

 вокруг оси ох.
вокруг оси ох.

 между точками их пересечения.
между точками их пересечения.
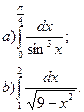
 вокруг оси ох
вокруг оси ох , проходящую через точку (2,0).
, проходящую через точку (2,0).



 в точке (1,2).
в точке (1,2).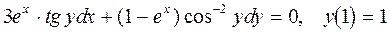














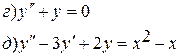





 , удовлетворяющую начальному условию у(0)=1.
, удовлетворяющую начальному условию у(0)=1.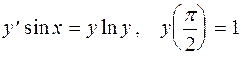


















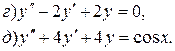
 , проходящую через точку (0,0).
, проходящую через точку (0,0).